Точечные оценки и их свойства

Статистическое оценивание параметров.

Статистические методы не позволяют точно вычислить неизвестные параметры теоретического распределения, они могут лишь оценить эти параметры.

Определение: Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых значений изучаемого признака.

Например, для оценки математического ожидания нормального распределения служит функция (среднее арифметическое наблюдаемых значений признака) 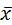=(x₁+x₂+…x_n)/n.

Статистические оценки бывают точечными или интервальными. Сначала рассмотрим точечные статистические оценки и их свойства.

(несмещенность, состоятельность и эффективность).

Определение: Несмещённой называют статистическую оценку θ*, математическое ожидание которой равно оцениваемому параметру θ при любом объёме выборки, т.е. M(θ*)= θ.

Определение: Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Определение: Эффективной называют статистическую оценку, которая (при заданном объёме выборки n) имеет наименьшую возможную дисперсию.

Определение: Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру: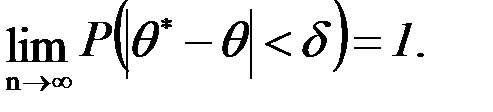

Например, если дисперсия D(X) несмещённой оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной.

Пусть θ* – статистическая оценка неизвестного параметра θ теоретического распределения. По выборке объема n найдена оценка θ*₁. Извлечем из генеральной совокупности другую выборку того же объёма n и по её данным найдем оценку θ*₂. Повторяя опыт многократно, получим числа θ*₁, θ*₂,…. θ*_к.

Таким образом, оценку θ* можно рассматривать как случайную величину, а числа θ*₁, θ*₂, …, θ*_к – как её возможные значения.

Дата добавления: 2014-12-27