Элементы, работающие на косой изгиб

3.21. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений элементов, работающих на косой изгиб, допускается производить, принимая форму сжатой зоны по черт. 3.3, при этом должно удовлетворяться условие

(3.26)

где М_х - составляющая изгибающего момента в плоскости оси х (за оси х и у принимаются две взаимно перпендикулярные оси, проходящие через точку приложения равнодействующей усилий в растянутой арматуре, параллельно сторонам сечения; для сечения с полкой ось х принимается параллельно плоскость ребра);

Черт.3.3. Форма сжатой зоны в поперечном сечении железобетонного элемента, работающего на косой изгиб

а - таврового сечения; б - прямоугольного сечения;

1 - плоскость действия изгибающего момента; 2 - точка приложения равнодействующей усилий в растянутой арматуре

A_web = A_b – A_ov; (3.27)

А_b - площадь сечения сжатой зоны бетона, равная:

; (3.28)

А_ov - площадь сечения наиболее сжатого свеса полки;

х ₁- размер сжатой зоны по наиболее сжатой стороне сечения, определяемый по формуле

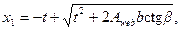(3.29)

здесь

(3.30)

S_ov,x - статический момент площади А_ov в плоскости оси х относительно оси у;

S_ov,y - то же, в плоскости оси у относительно оси х;

b_o - расстояние от равнодействующей усилий в растянутой арматуре до наиболее сжатого боковой стороны сечения (или грани ребра);

β - угол наклона плоскости действия изгибающего момента к оси х, т.е. ctg β = М_х /М_у;

S_sx, S_spx - статические моменты площади сечения соответственно напрягаемой и ненапрягаемой арматуры сжатой зоны относительно оси у.

При расчете прямоугольных сечений значения А_ov, S_ov,x и S_ov,y в формулах (3.26), (3.27) и (3.30) принимаются равными нулю.

Если А_b < А_ov или если х < 0,2 h'_f, расчет производится как для прямоугольного сечения шириной b = b'_f. Если выполняется условие

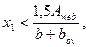(3.31)

где b_ov - ширина наименее сжатого свеса полки, расчет производится без учета косого изгиба, т.е. по формулам пп.3.12 и 3.17 на действие момента М = М_х;при этом следует проверить условие (3.34), принимая х ₁ как при косом изгибе.

Приведенную методику расчета следует применять, если относительная высота сжатой зоны, измеренная по нормали к границе сжатой зоны и определяемая по формуле (3.32), меньше или равна ξ_R (см. п.3.8):

(3.32)

где b'_ov - ширина наиболее сжатого свеса;

θ - угол наклона прямой, ограничивающий сжатую зону, к оси y;

значение tg θ определяется по формуле

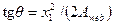(3.33)

где х ₁ - значение, вычисляемое по формуле (3.29) при γ_{s 3} = 1,0.

При проверке условия (3.26) коэффициент γ_{s 3}в формуле (3.28) определяется согласно п.3.9, при значении ξ принимаемом равным:

при отсутствии в сжатой зоне полки ξ = ξ ₁

при наличии в сжатой зоне полки ξ = (ξ ₁ + ξ_R) / 2.

Если выполняется условие

ξ ₁ > ξ_R (см. п.3.8), (3.34)

следует произвести повторный расчет с заменой в формуле (3.28) значения γ_{s 3} R_s напряжением σ_s, равным:

а) при ξ ≤ ξ_el

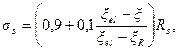(3.35)

где ξ_el - относительная высота сжатой зоны сечения, соответствующая напряжению арматуры растянутой зоны, равной 0,9 R_s, и определяемая по формуле 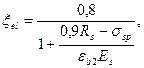(здесь ε_{b 2} = 0,0035 – предельная относительная деформация сжатого бетона) или по табл. 3.2;

б) при ξ > ξ_el

(3.36)

При арматуре растянутой зоны класса А540, если ξ ₁ > ξ_R используется только формула (3.36).

Расчет на косой изгиб производиться на основе нелинейной деформационной модели согласно пп.3.26-3.29, если соблюдаются условия:

для прямоугольных и тавровых сечений с полкой в сжатой зоне

х ₁ > h;

для двутавровых и тавровых сечений с полкой в растянутой зоне

х ₁ > h - h_f - b_ov,t tg θ,

где h_f, b_ov,t - высота и ширина наименее растянутого свеса полки (черт. 3.4).

При использовании формул настоящего пункта за растянутую арматуру площадью A_sp и A_s рекомендуется принимать арматуру, располагаемую вблизи растянутой грани, параллельной оси у, а за сжатую арматуру площадью A'_sp и A'_s - арматуру, располагаемую вблизи растянутой грани, параллельной оси у, но по одну наиболее сжатую сторону от оси х (см. черт. 3.3).

Черт. 3.4. Двутавровое сечение со сжатой зоной, заходящей в наименее растянутый свес полки

1-1 - плоскость действия изгибающего момента

Таблица 3.2

σsp / Rs	Значение ξel при растянутой арматуре классов
А600	А800	А1000	Вр1200	Вр1300	Вр1400	Вр1500	К1400	К1500
1,2	1,03	1,14	1,24	1,40	1,48	1,60	1,72	1,81	1,98
1,1	0,94	1,00	1,05	1,12	1,15	1,20	1,24	1,27	1,33
1,0	0,86	0,89	0,91	0,93	0,94	0,96	0,97	0,98	1,00
0,9	0,80	0,80	0,80	0,80	0,80	0,80	0,80	0,80	0,80
0,8	0,74	0,73	0,72	0,70	0,69	0,69	0,68	0,67	0,67
0,7	0,70	0,67	0,65	0,62	0,61	0,60	0,59	0,58	0,57
0,6	0,65	0,62	0,59	0,56	0,55	0,53	0,52	0,51	0,50
0,5	0,62	0,57	0,54	0,51	0,50	0,48	0,47	0,46	0,45
Примечание. Предварительное напряжение σsp принимается с учетом всех потерь и коэффициента γsp = 0,9.

Если арматура распределена по сечению, что не позволяет до расчета определить площадь и центры тяжести сечений растянутой и сжатой арматуры, расчет также производится на основе нелинейной деформационной модели согласно пп.3.26-3.29.

Дата добавления: 2014-12-27