Расчет нормальных сечений на основе нелинейной деформационной модели

3.26. При расчете по прочности усилия и деформации в нормальном сечении определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элементов, а также следующие положения:

- распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону (гипотеза плоских сечений, см. черт.3.14);

- связь между осевыми сжимающими напряжениями бетона σ_b и относительными его деформациями ε_b принимают в виде двухлинейной диаграммы (черт.3.10), согласно которой напряжения σ_b определяются следующим образом:

при 0 ≤ ε_b ≤ ε_{b 1, red} σ_b = E_b,red ε_b;

при ε_{b 1, red} < ε_b ≤ ε_{b 2} σ_b = R_b;

где E_b,red - приведенный модуль деформации бетона, равный

E_b,red = R_b / ε_{b 1, red} ;

ε_{b 1, red} = 0,0015;

ε_{b 2}= 0,0035;

R_b - см. табл.2.4;

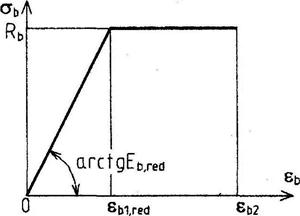
Черт.3.10. Двухлинейная диаграмма состояния сжатого бетона

- сопротивление бетона растянутой зоны не учитывается (т.е. принимается σ_b = 0,0);

- связь между напряжениями арматуры σ_s и относительными деформациями арматуры от внешней нагрузки ε_s принимают:

для ненапрягаемой арматуры с физическим пределом текучести (см.п.2.16) в виде двухлинейной диаграммы (черт 3.11), согласно которой напряжения σ_s принимают равными:

при 0 ≤ ε_s ≤ ε_{s 0} σ_s = E_s ε_s;

при ε_{s 0}< ε_s ≤ ε_{s 2} σ_s = R_s;

где ε_{s 0} = R_s / E_s

ε_{s 2} = 0,025;

R_s - см. табл.2.8;

E_s - см. п.2.24;

Черт.3.11. Двухлинейная диаграмма состояния арматуры с физическим пределом текучести

для ненапрягаемой арматуры с условным пределом текучести в виде трехлинейной диаграммы (черт.3.12), согласно которой напряжения σ_s принимают равными:

при 0 ≤ ε_s ≤ ε_{s 1} σ_s = E_s ε_s;

при ε_{s 1}< ε_s ≤ ε_{s 2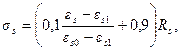} но не более 1,1 R_s,

где ε_{s 1} = 0,9 R_s / E_s

ε_{s 0} = R_s / E_s + 0,002;

ε_{s 2} = 0,015;

для напрягаемой арматуры любых видов связь между напряжениями σ_s и деформациями от внешней нагрузки ε_s принимают по вышеприведенными зависимостям, заменяя для стержней растянутой зоны значение ε_s на ε_s + σ_sp / E_s, где σ_sp -предварительное напряжение арматуры с учетом γ_sp = 0,9, а для стержней сжатой зоны ε_s на ε_s - σ_sp / E_s, где σ_sp принимается с учетом γ_sp =1,1; при этом для стержней растянутой зоны трехлинейная диаграмма σ_s - ε_s приобретает вид согласно черт.3.13.

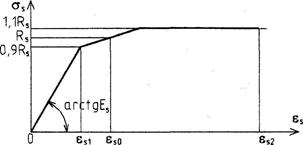
Черт.3.12. Трехлинейная диаграмма состояния арматуры с условным пределом текучести

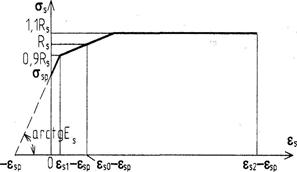
Черт.3.13. Трехлинейиая диаграмма состояния арматуры с условным пределом текучести при учете предварительного напряжения

(здесь ε_s - деформация арматуры от внешней нагрузки)

3.27. Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям рекомендуется осуществлять с помощью процедуры численного интегрирования по нормальному сечению. Для этого нормальное сечение в направлении плоскости изгиба (нормальной нейтральной оси) разделяется на участки малой ширины, напряжения в которых принимают равномерно распределенными и соответствующими деформациям на уровне середины ширины участка.

В общем случае положение нейтральной оси и максимальные деформации (черт.3.14) изгибаемых элементов определяют из уравнений равновесия внешних и внутренних усилии:

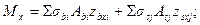(3.44)

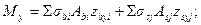(3.45)

(3.46)

где М_х и М_у - изгибающие моменты, действующие в плоскостях выбранных координатных осей соответственно х и у;

A_bi, z_bxi, z_byi, σ_bi - площадь, координаты центра тяжести i -того участка бетона и напряжение на уровне его центра тяжести;

A_sj, z_sxj, z_syj, σ_sj - площадь, координаты центра тяжести j -того стержня и напряжение в нем.

Напряжения σ_bi и σ_sj определяются в соответствии c диаграммами на черт.3.10-3.13.

Растягивающие напряжения арматуры σ_sj следует учитывать в уравнениях (3.44) - (3.46) со знаком "минус".

Координатные оси х и у рекомендуется проводить через центр тяжести наиболее растянутого стержня.

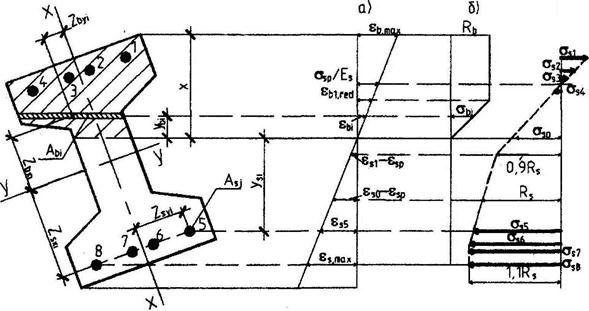
Черт.3.14. Эпюры деформаций и напряжений бетона и арматуры

а - эпюра деформаций; б – эпюра напряжений бетона; в - напряжения в стержнях напрягаемой арматуры с условным пределом текучести

3.28. Расчет сечении изгибаемых нормальных железобетонных элементов по прочности производят из условий

ε_{b , max} ≤ ε_{b 2}; (3.47)

│ ε_{s , max} │≤ ε_{s 2} - ε_sp, (3.48)

где ε_{b , max} и ε_{s , max} - относительные деформации соответственно наиболее сжатого волокна бетона и наиболее растянутого стержня арматуры от действия внешних нагрузок, определяемые из решения уравнений (3.44) - (3.46);

ε_sp – относительное удлинение напрягаемой арматуры при нулевых деформациях окружающего бетона, равное ε_sp = σ_sp/E_s, где σ_sp принимается с учетом γ_sp = 0,9;

ε_{b 2,} ε_{s 2} - см п.3.26.

3.29. Расчет на основе нелинейной деформационной модели производится с помощью компьютерных программ.

При действии в нормальном сечении двух моментов М_х и М_у по обеим координатным осям х и у компьютерную программу рекомендуется составлять на основе следующего алгоритма:

1. Задаются направлением нейтральной оси: в 1-м приближении это направление определяется как для упругого материала, т.е. принимается угол наклона нейтральной оси к оси у равным

2.Последовательными приближениями подбирают такую высоту сжатой зоны х (см. черт.3.14), при которой выполняется равенство (3.46); при этом в крайней сжатой точке принимается ε_b = ε_{b 2,} деформации сжатого бетона каждого i -того участка принимаются равными ε_bi = ε_{b 2} y_bi / х, а деформации j -того стержня арматуры – ε_sj = ε_{s 2} y_sj / х, где y_bi, y_sj - расстояния от нейтральной оси до центра тяжести соответственно i -того участка бетона и j -ого стержня арматуры. В случае, если ε_{s , max} > ε_{s 2} - ε_sp принимается ε_{s , max} = ε_{s 2} - ε_sp и тогда ε_bi = ε_{s , max} y_si /(h_o - х), где h_o – расстояние между наиболее растянутым стержнем арматуры и наиболее сжатой точкой бетона в направлении, нормальном нейтральной оси. Напряжения σ_bi и σ_sj определяются в зависимости от соответствующих деформаций ε_bi и ε_sj по диаграммам на черт.3.10-3.13.

3. По формулам (3.44) и (3.45) определяют моменты внутренних усилий M_x,ult и М_y,ult. Если оба эти момента оказываются больше или меньше соответствующих внешних моментов М_х и М_у, то прочность сечения считается соответственно обеспеченной или необеспеченной.

Если один из моментов (например М_y,ult)меньше соответствующего внешнего момента (т.е. М_y,ult < М_у), а другой больше (т.е. M_x,ult > М_х), задаются другим углом наклона нейтральной оси θ (большим, чем ранее принятый) и вновь проводят аналогичный расчет.

Дата добавления: 2014-12-27