Примеры расчета

Пример 11. Дано: железобетонная плита перекрытая с размерами поперечного сечения по черт 3.22; бетон класса В25 (R_b = 14,5 МПа; R_bt = 1,05 МПа); ребро плиты армировано плоским каркасом с поперечными стержнями из арматуры класса В500 диаметром 5 мм (A_sw = 19,6 мм²; R_sw = 300 МПа) шагом s_w = 200 мм; усилие обжатия от продольной арматуры в ребре Р = 170 кН; расчетная нагрузка, приходящаяся на половину сечения плиты q = 23 кН/м; временная часть нагрузки q_v = 19 кН/м; поперечная сила в опорном сечении ребра Q_max = 55 кН.

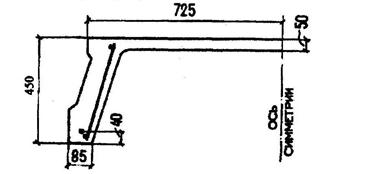
Черт.3.22. К примеру расчета 11

Требуется проверить прочность по бетонной полосе между наклонными сечениями, а также прочность по наклонным сечениям на действие поперечных сил.

Р а с ч е т. Из черт 3.22 имеем h_o = 450 - 40 = 410 мм, b = 85 мм.

Прочность бетонной полосы проверяем из условия (3.49).

0,3 R_bbh_o = 0,3·14,5·85·410 = 151600 H = 151,6 кH > Q_max = 55 кН.

т.е. прочность бетонной полосы обеспечена.

Прочность по наклонным сечениям проверяем из условия (3.50).

По формуле (3.55) определим

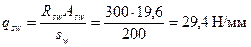
По формуле (3.53а) определяем коэффициент φ_n. Для этого, принимая А₁ = b · h = 85·450 = 38250 мм², вычислим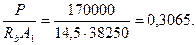

Тогда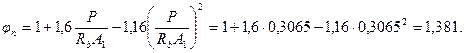

Проверим условие (3.56)

0,25 φ_nR_btb = 0,25·1,381·1,05·85 = 30,85 Н/мм > q_sw = 29,4 Н/мм,

т.е. условие (3.56) не выполняется, и тогда принимаем φ_nR_btb = 4 q_sw, что соответствует M_b = 6 q_swh_o² = 6·29,4·410² = 29,65·10⁶ Н·мм; Q_b,min = 2 q_swh_o = 2·29,4·410 = 24108 Н; 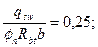при этом c_o= 2 h_o = 2·410 = 820мм.

Определяем длину проекции с не выгоднейшего наклонного сечения согласно п.3.33.

q ₁ = q – 0,5 q_v = 23 - 0,5·19 = 13,5 кН/м (Н/мм).

Так как 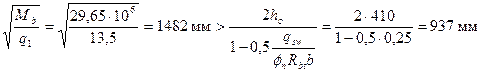, принимаем 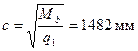, но 3 h_o = 3·410 = 1230 мм < с, принимаем с = 3 h_o = 1230 мм, что соответствует Q_b = Q_b,min = 24108 Н = 24,1 кН.

Проверяем условие (3.50), принимая Q в конце наклонного сечения, т.е. Q = Q_max – q ₁ c = 55 - 13,5·1,23 = 38,4 кН:

Q_b + 0,75 q_swc_o = 24,1 + 0,75·29,4·0,82 = 42,2 кН > Q = 38,4 кН,

т.е. прочность любого наклонного сечения обеспечена.

Согласно п. 3.36 определим S_w,_max, заменяя φ_nR_bb на 4 q_sw

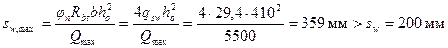
и кроме того s_w < h_o /2 = 410/2 = 205 мм, т.е. требования п.5.12 выполнены.

Пример 12. Дано:свободно опертый железобетонный ригель перекрытия пролетом l = 8,3 м нагружен равномерно распределенной нагрузкой: временной эквивалентной q_v = 114 кН/м и постоянной q_g = 46 кН/м; размеры поперечного сечения b = 300 мм, h = 800 мм, h_o = 700 мм; бетон класса В30 (R_b = 17 МПа; R_bt = 1,15 МПа) хомуты сварные из арматуры класса А400 (R_sw = 285 МПа); усилие предварительного обжатия Р = 1600 кН.

Требуется определить диаметр и шаг хомутов у опоры, а также выяснить на каком расстоянии от опоры и как может быть увеличен их шаг.

Расчет. Наибольшая поперечная сила в опорном сечении равна:

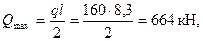
(здесь q = q_v + q_g = 114 + 46 = 160 кН/м).

Определим требуемую интенсивность хомутов приопорного участка согласно п.3.34,б.

По формуле (3.53а) определим коэффициент φ_n, принимая

A ₁= bh = 300·800 = 240000 мм² и ,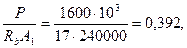

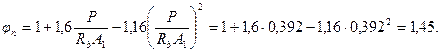
Из формулы (3.52) имеем

M_b = 1,5 φ_nR_btbh_o² = 1,5·1,45·1,15·300·700² =367,7·10⁶ Н·мм = 367,7 кН·м;

q₁ = q_g + 0,5 q_v = 46 +114/2 = 103 кН/м (Н/мм);

.

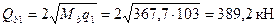Так как 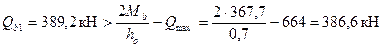, интенсивность хомутов определяем по формуле (3.59):

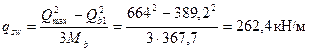
При этом, поскольку Q_{b 1}= 389,2 кН > φ_nR_bbh_o = 1,45·1,15·300·700 = 350200 Н = 350,2кН, оставляем q_sw = 262,4 Н/мм.

Проверим условие (3.56):

0,25 φ_nR_btb = 0,25·1,45·1,05·300 = 125 Н/мм < q_sw,

т.е. это условие выполняется.

Согласно п.5.12 шаг хомутов у опоры должен быть не более 0,5 h_o = 350 мм и не более 300 мм, а в пролете не более 3/4 h_o = 525 мм. Максимальный шаг хомутов у опоры согласно формуле (3.67) равен

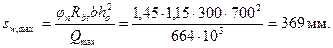
Принимаем шаг хомутов у опоры s ₁=250 мм, а в пролете - s ₂ = 2 s ₁ = 500 мм.

Отсюда .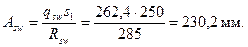

Принимаем в поперечном сечении три хомута диаметром 10 мм (А_{sw 1} = 236 мм²).

Тогда ;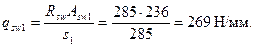

q_{sw 2} = 0,5 q_{sw 1} = 0,5·269 = 134,5 Н/мм > 0,25 φ_nR_btb = 125 Н/мм.

Длину участка с наибольшей интенсивностью хомутов q_{sw 1} определяем согласно п. 3.35.

Так как Δ q_sw = 0,75(q_{sw 1}- q_{sw 2} )= 0,75·134,5 = 100,9 Н/мм < q ₁ = 103 Н/мм, значение с равно

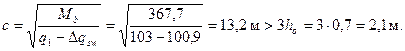
Принимаем с = 2,1 м и с_o = 2 h_o = 2·0,7 = 1,4 м. Тогда

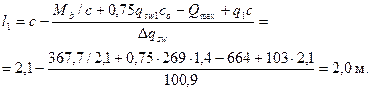
Принимаем длину приопорного участка с шагом хомутов s_w = 250 мм не менее 2 м.

Пример 13. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт.3.23,а; размеры поперечного сечения - по черт.3.23,б; бетон класса В50 (R_bt = 1,6 МПа, R_b = 27,5 МПа); хомуты из арматуры класса А400 (R_sw = 285 МПа); усилие предварительного обжатия Р = 640 кН.

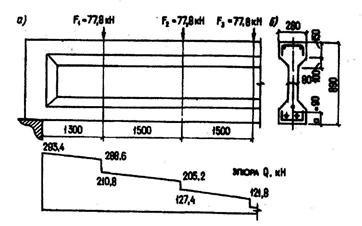
Черт. 3.23. К примеру расчета 13

Требуется определить диаметр и шаг хомутов, а также выяснить на каком расстоянии и как может быть увеличен их шаг,

Расчет. Согласно черт.3.23,б имеем: b = 80 мм, h = 890 мм, h_о = 890 - 90 = 800 мм. По формуле (3.53а) определим коэффициент φ_n принимая A ₁= bh = 80·890 = 71200 мм² и ;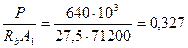

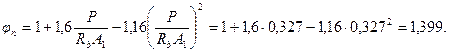
Определим требуемую интенсивность хомутов согласно п.3.34,а, принимая длину проекции наклонного сечения с, равной расстоянию от опоры до первого груза – с ₁= 1,3 м. Тогда a ₁ = c ₁/ h_o = 1,3/0,8 = 1,625 < 2,0, и следовательно, а ₀₁ = а ₁ = 1,625.

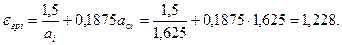
Поперечная сила на расстоянии с ₁от опоры равна Q ₁ = 288,6 кН (см. черт.3.23,а).

Поскольку 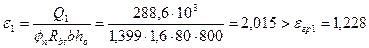, значение q_{sw (1)}определяем по формуле (3.58)

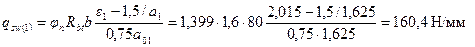
Определим значение q_{sw (2)} при значении с, равном расстоянию от опоры до второго груза –с ₂ = 2,8 м.

a ₂ = с ₂/ h_о =2,8/0,8 = 3,5 > 2,0, следовательно, а ₀₂=2,0.

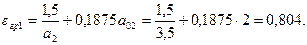
Соответствующая поперечная сила равна Q ₂ = 205,2 кН.

Поскольку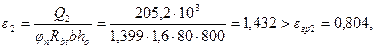

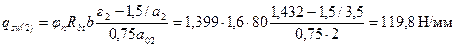
Принимаем максимальное значение q_sw = q_{sw (1)} = 160,4 Н/мм.

Согласно п.5.12 шаг s_{w 1} у опоры должен быть не более 0,5 h_o = 400 мм и не более 300 мм, а в пролете - не более 3/4 h = 600 мм. Максимально допустимый шаг у опоры согласно формуле (3.67) равен

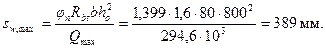
Принимаем шаг у опоры s_{w 1}= 200 мм, а в пролете s_{w 2}= 2 s_{w l} = 400 мм.

Отсюда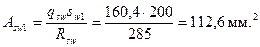

Принимаем одноветвевые хомуты диаметром 12 мм (А_sw = 113,1 мм²).

Длину участка с шагом хомутов s_{w 1}определяем из условия обеспечения прочности согласно п.3.35. При этом 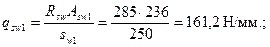q_{sw 2} = 0,5 q_{sw 1} = 80,6 Н/мм; q_{sw 1} - q_{sw 2} = q_{sw 2} = 80,6 Н/мм.

Зададим длину участка с шагом хомутов s_{w 1}равной расстоянию от опоры до второго груза l ₁= 2,8 м и проверим условие (3.50) при значении с,равном расстоянию от опоры до третьего груза: с = 4,3 м > l ₁.

Поскольку 2 h_o + l ₁= 2·0,8 + 2,8 = 4,4 м > с =4,3 м, значение Q_sw определяем по формуле (3.63), принимая с_o = 2 h_o = 1,6м,

Q_sw = 0,75[ q_{sw 1} с_о - (q_{sw 1}- q_{sw 2} )(c - l ₁)] = 0,75[161,2·1,6 - 80,6(4,3 - 2,8)] = 102,8 кН.

При с = 4,3 м > 3 h_o = 3·0,8 = 2,4 м значение Q_b соответствует его минимальному значению Q_b = Q_b,тiп = 0,5 φ_nR_btbh_o = 0,5·1,399·1,6·80·800 = 71629 Н = 71,6 кН. Соответствующая поперечная сила равна Q ₃ = 121,8 кН (см. черт.3.23,а).

Q_b + Q_sw = 71,6 + 102,8 = 174,4 кН > Q ₃= 121,8 кН, т.е. прочность наклонного сечения обеспечена.

Таким образом, длину приопорных участков с шагом хомутов 200 мм принимаем равной l = 2,8 м при шаге хомутов 400 мм в пролетном участке.

Пример 14. Дано: плита перекрытия с растянутой гранью, наклонной к горизонтали, с размерами по черт.3.24; бетон класса В40 (R_b = 22 МПа, R_bt =1,4 МПа); одноветвевые хомуты из арматуры класса А400 (R_sw = 285 МПа) диаметром 10 мм (A_sw = 78,5 мм²) и шагом s_w =100 мм; усилие предварительного обжатия Р = 980 кН; временная эквивалентная нагрузка q_v = 24,2 кН/м; постоянная нагрузка q_g = 7,8 кН/м; поперечная сила на опоре Q_max =186 кН.

Требуется проверить прочность наклонного сечения по поперечной силе.

Расчет ведем согласно п.3.38.

Из черт.3.24 имеем h_{o 1} = 300 - 75 = 225 мм. Размер b принимаем на уровне середины высоты опорного сечения

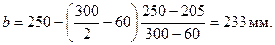
По формуле (3.53а) определим коэффициент φ_n, принимая A ₁по опорному сечению A ₁= bh = 233·300 = 69900 мм² и ;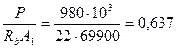

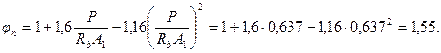
Тогда φ_nR_btb = 1,55·1,4·233 = 505,6 Н.

По формуле (3.55) определяем

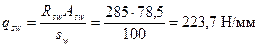
Значение tg β согласно черт.3.24,а равно

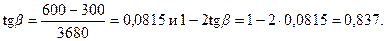
q ₁ = q_g + 0,5 q_v = 7,8+0,5·24,2 = 19,9 кН/м.

По формуле (3.68) определяем проекцию невыгоднейшего наклонного сечения

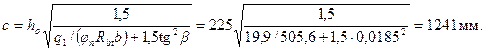
При этом

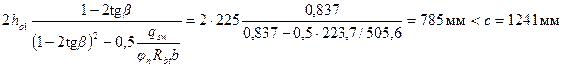
и следовательно, оставляем с = 1241 мм, но поскольку 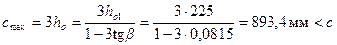принимаем с = с_так = 893,4 мм. Тогда h_o = с_так /3 = 893,4/3 = 297,8 мм.

Ширина ребра на уровне середины высоты h = h_o + a =298 + 75 = 373 мм равно , и тогда A ₁= bh = 226·373 = 84298 мм² и ;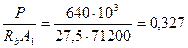

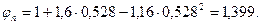
Поскольку с = с_так, Q_b = Q_b,тiп = 0,5 φ_nR_btbh_o =0,5·1,52·1,4·226·298 = 71,6·10³ Н = 71,6 кН.

Проверим условие (3.50), принимая Q_sw = 0,75 q_swс_о = 0,75·223,7·596 = 99994 Н ≈ 100 кН и Q = Q_тax - q ₁ c = 19,9·0,893 = 168,2 кН.

Q_b + Q_sw = 71,6 + 100 = 171,6 кН > Q = 168,2 кН,

т.е. прочность наклонных сечений обеспечена.

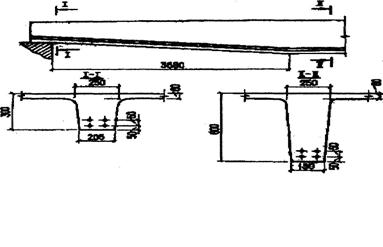
Черт.3.24. К примеру расчета 14

Пример 15. Дано: железобетонная двускатная балка с размерами по черт.3.25,а загружена сосредоточенными силами от плит покрытия и подвесных кранов, как показано на черт.3.25,б; бетон класса В40 (R_b = 22 МПа, R_bt = 1,4 МПа); хомуты двухветвевые из арматуры класса А400 (R_sw = 285 МПа) диаметром 10 мм (A_sw = 157 мм²) и шагом s_w = 100 мм; усилие предварительного обжатия Р = 1220 кН.

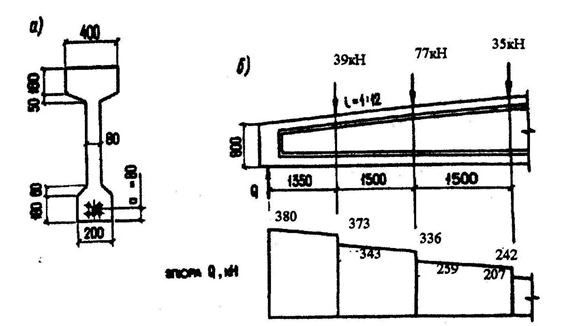
Черт.3.25. К примеру расчета 15

Требуется проверить прочность наклонных сечений по поперечной силе.

Расчет ведем согласно п.3.38. Проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до первого груза с ₁ = 1,35 м. Согласно черт.3.25,б tg β = 1/12.

Высота поперечного сечения в конце наклонного сечения равна

h = 800 +1350/12 = 912 мм.

Определим значение φ_n для этого сечения согласно п.3.32:

А₁ = b · h + (b_f - b) b_f = 80·912 + (200 - 80) ·210 = 98160 мм²;

;

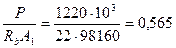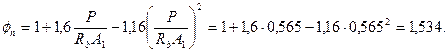
Значение q_sw равно .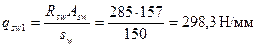

Рабочая высота опорного сечения равна h _o1 = 800 - 80=720 мм.

Поскольку значение

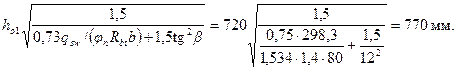
меньше с ₁=1350 мм, принимаем с ₁= 770 мм.

Полная и рабочая высота поперечного сечения на расстоянии с ₁= 770 мм от опоры равны

h = 800 + 770/12 = 864,2 мм; h_o = 864,2 - 80 = 784,2 мм.

Определим значение φ_n для этого сечения: А₁ = 80·864,2 + 120·210 = 94336 мм²; ,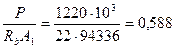

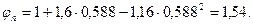
Тогда .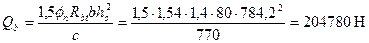

Принимая с_о = с = 770 мм < 2 h_o, имеем

Q_sw = 0,75 q_swс_о = 0,75·298,3·770 = 172268 Н. Проверяем условие (3.50), принимая значение Q на расстоянии с ₁ = 0,77 м от опоры равным

:

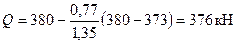Q_b + Q_sw = 204,8 + 172,3 = 376,1 кН > Q = 376 кН, т.е. прочность этого наклонного сечения обеспечена.

Проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до второго груза - с₂ = 2,85 м.

Полная и рабочая высота поперечного сечения на расстоянии 2,85 м от опоры равны

h = 800 + 2850/12 = 1037 мм; h_о = 1037 - 80 - 957 мм.

Поскольку 3 h_o = 3·957 - 2871 мм > с ₂, оставляем с ₂ = 2,85 м.

Аналогично определяем значение φ_n:

А₁ = 80·1037 + 33600 = 116560 мм²;

,

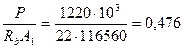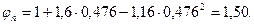
Согласно п.3.32 определяем Q_b

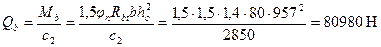
Определяем Q_sw, принимая c_o = 2 h_o =2·957 = 1914 мм < с ₂ = 2850 мм.

Q_sw = 0,75 q_swс_о = 0,75·298,3·1914 = 434250 Н.

Q_b + Q_sw = 80980 + 434250 = 515230 Н = 515,2 кН > Q ₂= 336 кН.

т.е. прочность этого сечения также обеспечена.

Пример 16. Дано: многопустотная плита перекрытия пролетом l = 5,85 м с поперечным сечением по черт 3.26; бетон класса В25 (R_b = 14,5 МПа, R_bt = 1,05 МПа, Е_b = 30·10³ МПа); усилие обжатия Р = 215 кН; временная эквивалентная нагрузка q_v = 6 кН/м²; нагрузка от собственного веса плиты и пола q_g = 5,2 кН/м².

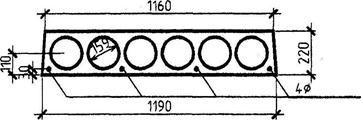
Черт.3.26. К примеру расчета 16

Требуется выяснить, необходима ли в плите поперечная арматура.

Расчет. Проверим условия прочности согласно п.3.40. Рабочая высота сечения h_o = 220 - 30 = 190 мм.

При ширине плиты 1,2 м нагрузки на 1 п. м плиты равны:

q = (q_g + q_v)1,2= (5,2 + 6,0)l,2 = 13,44 кН/м;

q ₁= (q_g + 0,5 q_v)1,2= (5,2 + 3,0)l,2 = 9,84 кН/м.

Поперечная сила в опорном сечении .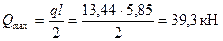

Проверим условие (3.70), принимая минимальную ширину сечения, т.е. b = 1175-6·159 = 221 мм:

2,5 R_btbh_o = 2,5·1,05·221·190 = 110,2·10³ Н = 110,2 кН > Q_max = 39,3 кН, т.е. условие (3.70) выполняется.

Проверим условие (3.71), принимая значение с равным М_b / Q_crc. Для этого определим геометрические характеристики приведенного сечения, принимая a = E_s/E_b = 2·10⁵/3·10⁴ = 6,67 и A_sp = 616 мм² (4Æ14):

площадь

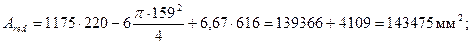
расстояние от центра тяжести до низа

y = (139366·110+4109·30)/143475 = 107,7 мм;

момент инерции

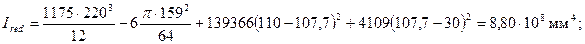
статический момент части сечения, расположенной выше оси, проходящей через центр тяжести

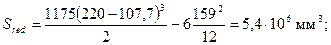
Тогда согласно формуле (3.72)

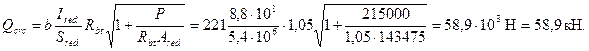
Поскольку Q_max = 39,3 кН < Q_crc = 58,9 кН, прочность наклонного сечения с длиной проекции с = Мь / Q_crc заведомо обеспечена.

Проверим условие (3.71), принимая значение с равным длине приопорного участка l ₁ без нормальных трещин. Значение l ₁определим из решения уравнения

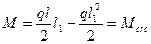
Определим момент М_сrс согласно п.4.5, принимая 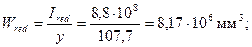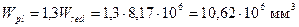и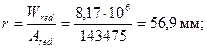

e₀ = y - a = 107,7 - 30 = 77,7 мм;

М_сrс = R_btW_pl + P (e₀ + r) = 1,05·10,62·10⁶ + 215000(77,7 + 56,9) = 40,09·10⁶ Н·мм = 40,1 кН·м.

Из вышеприведенного квадратного уравнения находим с = l ₁:

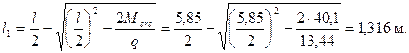
Определяем коэффициент φ_n согласно п.3.32.

Ширину свесов сжатой полки определим как сумму сторон квадратов а_к, эквивалентных по площади сечению пустот, а их толщину h'_f как расстояние между эквивалентным квадратом и верхней гранью, т.е.

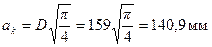; b'_f -b = 6а_k = 6·140,9 = 845,4 мм;

h'_f = (h - а_k)/2 = (220 -140,9)/2 = 39,5 мм.

Тогда А₁ = А - (b'_f - b) h'_f = 139366 - 845,5·39,5 = 105970 мм²;

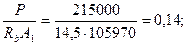
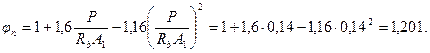
Поскольку с = l ₁ = 1,316 м > 3 h_o = 3·0,19 = 0,57 м, принимаем Q_b = Q_b,тiп = 0,5 φ_nR_btbh_o = 0,5·1,201·1,05·221·190 = 26,48·10³ Н = 26,48 кН.

Поперечная сила в конце наклонного сечения равна

Q = Q_тax - q ₁ c = 39,3 - 9,84·1,316 = 26,36 кН < Q_b = 26,48 кН

т.е. условие (3.71) выполняется для любых наклонных сечений. Следовательно, поперечную арматуру в плите можно не устанавливать.

Пример 17. Требуется по данным примера 11 проверить прочность наклонных сечений на действие изгибающего момента, принимая растянутую продольную арматуру ребра плиты в виде одного напрягаемого стержня класса А800 диаметром 22 мм (R_s = 695 МПа, A_sp = 380 мм²) и одного ненапрягаемого стержня класса В500 диаметром 5 мм (R_s = 415 МПа, A_s = 19,6 мм²); оба стержня анкеров не имеют; длина площадки опирания l_sup = 150 мм.

Расчет производим согласно пп.3.41-3.44. Поскольку продольная арматура не имеет анкеров, усилие в этой арматуре N_s определяем согласно п. 3.43.

Определим коэффициент влияния поперечного обжатия бетона а, принимая 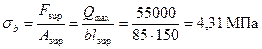.Поскольку 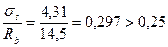, принимаем а = 0,75.

По формуле (3.78) определяем длину зоны анкеровки напрягаемого стержня, принимая η ₁= 2,5, η ₂= 1,0, d_s = 22 мм;

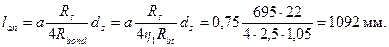
Для этого стержня l_s = l_sup = 150 мм, тогда

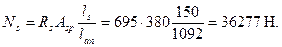
Аналогично определяем длину зоны анкеровки ненапрягаемого стержня, принимая η ₁=2,0, d_s = 5 мм:

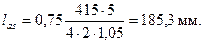
Для этого стержня l_s = l_sup - 10 = 140 мм, тогда

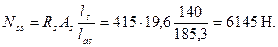
Итого полное значение N_s равно N_s = 36277 + 6145 = 42422 Н.

Принимая ширину сжатой грани b = b'_f = 725 мм, определяем плечо внутренней пары сил:

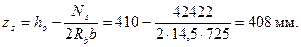
Тогда М_s = N_sz_s = 42422·408 = 17,3·10⁶ Н·мм = 17,3 кН·м.

Из примера 11 имеем q_sw = 29,4 Н/мм и q = 23 Н/мм. Определим длину проекции невыгоднейшего наклонного сечения по формуле (3.79)

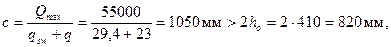
следовательно, принимаем с = 2/ h_o = 820 мм и тогда

М_sw = 0,5 q_swc ² = 0,5·29,4·820² = 9,844·10⁶ Н·мм = 9,88 кН·м.

За расчетный момент принимаем изгибающий в нормальном сечении, проходящем через конец наклонного сечения, т.е. на расстоянии (l_y + с)от точки приложения опорной реакции (где l_y = l _sup/3 = 50 мм черт. 3.27).

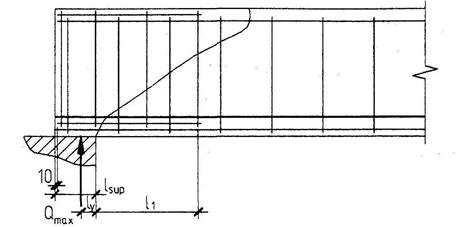
Черт. 3.27. К примеру расчета 17

,

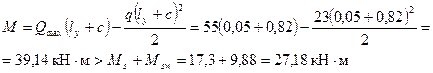т.е. прочность наклонного сечения на действие изгибающего момента не обеспечена.

Добавляем на приопорном участке дополнительный каркас длиной l ₁ = 400 мм с поперечными стержнями Æ8 А400 шагом 200 мм. Тогда добавочное поперечное армирование, выраженное через Δ q_sw, равно

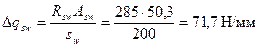
а q_{sw 1} = q_sw + Δ q_sw = 29,4 + 71,7 = 101,1 Н/мм.

Проекция невыгоднейшего наклонного сечения равна

.

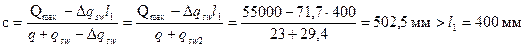Значение М_sw определяем по формуле (3.76)

M_sw = 0,5q_sw1c²- 0,5Δ q_sw (c - l ₁)²= 0,5·101,1·502,5² - 0,5·71,7(502,5 - 400)² = 13,14·10⁶ Н·м = 13,14 кН·м.

l_у + с = 0,05 + 0,50 = 0,55 м.

М = 55·0,55 - 12·0,557²/2 = 26,77 кН·м < M_s + М_sw = 30,44 кН·м. т.е. прочность наклонного сечения обеспечена.

Дата добавления: 2014-12-27