Отклонение

Моменты. Дисперсия. Среднее квадратическое

Кроме характеристик положения — средних, типичных значений случайной величины — употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяются так называемые моменты.

Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Совершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.

Начальным моментом s-го порядка прерывной случайной величины X называется сумма вида

(11.4)

Очевидно, это определение совпадает с определением начального момента порядка s в механике, если на оси абсцисс в точках x ₁, х ₂, …, x _n сосредоточены массы p ₁, р ₂, …, p _n. Для непрерывной случайной величины X начальным моментом s -го порядка называется интеграл

(11.5)

Нетрудно убедиться, что введенная в предыдущем пункте основная характеристика положения — математическое ожидание — представляет собой не что иное, как первый начальный момент случайной величины X.

Пользуясь знаком математического ожидания, можно объединить две формулы (11.4) и (11.5) в одну. Поэтому можно написать общее определение начального момента s -го порядка, справедливое как для прерывных, так и для непрерывных величин:

a_s [X] = M [X^s],

т.е. начальным моментом s-го порядка случайной величины X называется математическое ожидание s-й степени этой случайной величины.

Перед тем как дать определение центрального момента, введем новое понятие «центрированной случайной величины».

Пусть имеется случайная величина X с математическим ожиданием m _x. Центрированной случайной величиной, соответствующей величине X, называется отклонение случайной величины X от ее математического ожидания:

Условимся в дальнейшем везде обозначать центрированную случайную величину, соответствующую данной случайной величине, той же буквой со значком ° наверху.

Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю. Действительно, для прерывной величины

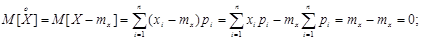
аналогично и для непрерывной величины.

Центрирование случайной величины, очевидно, равносильно переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию.

Моменты центрированной случайной величины носят название центральных моментов. Они аналогичны моментам относительно центра тяжести в механике.

Таким образом, центральным моментом порядка s случайной величины X называется математическое ожидание s -й степени соответствующей центрированной случайной величины:

Для прерывной случайной величины s -й центральный момент выражается суммой

а для непрерывной — интегралом

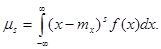
В дальнейшем в тех случаях, когда не возникает сомнений, к какой случайной величине относится данный момент, мы будем для краткости вместо a_s[X] и m_s[X] писать просто a_s и m_s.

Очевидно, для любой случайной величины центральный момент первого порядка равен нулю:

так как математическое ожидание центрированной случайной величины всегда равно нулю.

Выведем соотношения, связывающие центральные и начальные моменты различных порядков. Вывод мы проведем только для прерывных величин; легко убедиться, что точно те же соотношения справедливы и для непрерывных величин, если заменить конечные суммы интегралами, а вероятности — элементами вероятности.

Рассмотрим второй центральный момент:

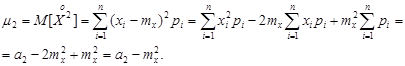
Аналогично для третьего центрального момента получим:

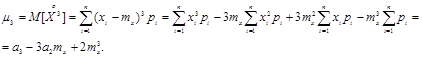
Выражения для m₄, m₅ и т.д. могут быть получены аналогичным путем.

Таким образом, для центральных моментов любой случайной величины X справедливы формулы:

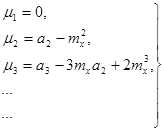(11.6)

Вообще говоря, моменты могут рассматриваться не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки а:

g_s = M [(X - a)^s]. (11.7)

Однако центральные моменты имеют перед всеми другими преимущество: первый центральный момент, как мы видели, всегда равен нулю, а следующий за ним, второй центральный момент при этой системе отсчета имеет минимальное значение. Докажем это. Для прерывной случайной величины X при s = 2 формула (11.7) имеет вид

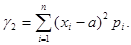
Преобразуем это выражение

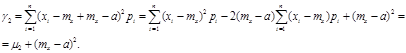
Очевидно, эта величина достигает своего минимума, когда m_x = a, т.е. когда момент берется относительно точки m_x.

Из всех моментов в качестве характеристик случайной величины чаще всего применяются первый начальный момент (математическое ожидание) m_x=a₁ и второй центральный момент m₂.

Второй центральный момент называется дисперсией случайной величины. Ввиду крайней важности этой характеристики среди других моментов введем для нее специальное обозначение D[X]:

m₂ = D [X].

Согласно определению центрального момента

, (11.8)

т.е. дисперсией случайной величины X называется математическое ожидание квадрата соответствующей центрированной величины.

Заменяя в выражении (11.8) величину ее выражением, имеем

. (11.9)

Для непосредственного вычисления дисперсии служат формулы:

- соответственно для прерывных и непрерывных величин.

Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания. Само слово «дисперсия» означает «рассеивание».

Если обратиться к механической интерпретации распределения, то дисперсия представляет собой не что иное, как момент инерции заданного распределения масс относительно центра тяжести (математического ожидания).

Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе — «стандартом») случайной величины X. Среднее квадратическое отклонение будем обозначать s [X]:

(11.10)

Для упрощения записей мы часто будем пользоваться сокращенными обозначениями среднего квадратического отклонения и дисперсии: s_x и D_x. В случае, когда не возникает сомнения, к какой случайной величине относятся эти характеристики, мы будем иногда опускать значок х у s_x и D_x и писать просто s и D. Слова «среднее квадратическое отклонение» иногда будем сокращенно заменять буквами с.к.о.

На практике часто применяется формула, выражающая дисперсию случайной величины через ее второй начальный момент. В новых обозначениях она будет иметь вид

Математическое ожидание m_x и дисперсия D_x (или среднее квадратическое отклонение s_ч) — наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения применяются моменты высших порядков.

Третий центральный момент служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания (или,. в механической интерпретации, масса распределена симметрично относительно центра тяжести), то все моменты нечетного порядка (если они существуют) равны нулю. Действительно, в сумме

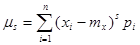
при симметричном относительно m_x законе распределения и нечетном s каждому положительному слагаемому соответствует равное, ему по абсолютной величине отрицательное слагаемое, так что вся сумма равна нулю. То же, очевидно, справедливо и для интеграла

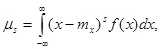
который равен нулю как интеграл в симметричных пределах от нечетной функции.

Естественно поэтому в качестве характеристики асимметрии распределения выбрать какой-либо из нечетных моментов. Простейший из них есть третий центральный момент. Он имеет размерность куба случайной величины; чтобы получить безразмерную характеристику, третий момент m₃ делят на куб среднего квадратического отклонения. Полученная величина носит название «коэффициента асимметрии» или просто «асимметрии»; мы обозначим ее Sk:

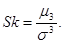(11.11)

На рис. 11.8 показано два асимметричных распределения; одно из них (кривая I) имеет положительную асимметрию (Sk > 0); другое (кривая II) — отрицательную (Sk < 0).

Четвертый центральный момент служит для характеристики так называемой «крутости», т.е. островершинности или плосковершинности распределения. Эти свойства распределения описываются с помощью так называемого эксцесса. Эксцессом случайной величины X называется величина

(11.12)

Число 3 вычитается из отношения 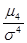потому, что для весьма важного и широко распространенного в природе нормального закона распределения (с которым мы подробно познакомимся в дальнейшем) . Таким образом, для нормального распределения эксцесс равен нулю; кривые, более островершинные по сравнению с нормальной, обладают положительным эксцессом; кривые более плосковершинные — отрицательным эксцессом.

На рис. 11.9 представлены: нормальное распределение (кривая I), распределение с положительным эксцессом (кривая II) и распределение с отрицательным эксцессом (кривая III).

Кроме рассмотренных выше начальных и центральных моментов, на практике иногда применяются так называемые абсолютные моменты (начальные и центральные), определяемые формулами:

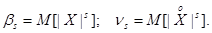
Очевидно, абсолютные моменты четных порядков совпадают с обычными моментами.

Из абсолютных моментов наиболее часто применяется первый абсолютный центральный момент

называемый средним арифметическим отклонением. Наряду с дисперсией и средним квадратическим отклонением среднее арифметическое отклонение иногда применяется как характеристика рассеивания.

Математическое ожидание, мода, медиана, начальные и центральные моменты и, в частности, дисперсия, среднее квадратическое отклонение, асимметрия и эксцесс представляют собой наиболее употребительные числовые характеристики случайных величин. Во многих задачах практики полная характеристика случайной величины — закон распределения — или не нужна, или не может быть получена. В этих случаях ограничиваются приблизительным описанием случайной величины с помощью числовых характеристик, каждая из которых выражает какое-либо характерное свойство распределения.

Очень часто числовыми характеристиками пользуются для приближенной замены одного распределения другим, причем обычно стремятся произвести эту замену так, чтобы сохранились неизменными несколько важнейших моментов.

Применимо к информационным блокам системы (модулям) понятия математического ожидания и дисперсии допустимо трактовать следующим образом: математическое ожидание – усредненный размер смысловых (тематических) модулей системы, измеряемый в байтах. Определим дисперсию как максимальное отклонение реального размера модуля от математического ожидания, или разница размеров максимально большого (максимально маленького) блока системы и математического ожидания.

При обработке предметной области ИС размер минимального смыслового информационного блока (модуля) "Понятие – полнотекстовое описание" должен выбираться исходя из следующих соображений:

· в блоке должна присутствовать необходимая информация для раскрытия основных свойств выбранного понятия;

· требуемое время загрузки данных должно составлять максимум 10 секунд (5 в среднем), поскольку больший интервал загрузки данных будет вызывать недовольство пользователей системы;

· большинство российских пользователей для подключения к Интернет пользуются модемными соединениями через интернет-провайдеров, что ограничивает обеспечивает скорость передачи данных от 19200 бит/с до 56000 бит/с (33600 бит/с в среднем).

Дата добавления: 2014-12-27