Энтропия сложной системы. Теорема сложения энтропий

На практике часто приходится определять энтропию для сложной системы, полученной объединением двух или более простых систем.

Под объединением двух систем X и Y с возможными состояниями x ₁, …, x _n; y ₁, …, y_m понимается сложная система (X, Y), состояния которой (x_i, y_i) представляют собой все возможные комбинации состояний x_i, y_i систем X и Y.

Очевидно, число возможных состояний системы (X, Y) равно n ´ m. Обозначим через P_ij вероятность того, что система (X, Y) будет в состоянии (x_i, y_j):

P_ij = P ((X ~ x_i)(Y ~ y_j)).

Вероятности P_ij удобно расположить в виде таблицы (матрицы).

yj xi	x1	x2	…	xn
y1	P11	P21	…	Pn1
y2	P12	P22	…	Pn2
. . .	. . .	. . .	… … …	. . .
ym	P1m	P2m	…	Pnm

Найдем энтропию сложной системы. По определению она равна сумме произведений вероятностей всех возможных ее состояний на их логарифмы с обратным знаком:

,

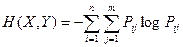или в других обозначениях:

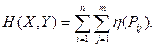
Энтропию сложной системы, как и энтропию простой, тоже можно записать в форме математического ожидания:

H (X, Y) = M [- log P (X, Y)], (12.6)

где log P (X. Y) — логарифм вероятности состояния системы, рассматриваемый как случайная величина (функция состояния).

Предположим, что системы X и Y независимы, т.е. принимают свои состояния независимо одна от другой, и вычислим в этом предположении энтропию сложной системы. По теореме умножения вероятностей для независимых событий

P (X, Y) = P (X)P(Y),

откуда

log P(X, Y) = log P(X)+ log P(Y).

Подставляя в (12.6), получим

H (X, Y) = M [- log P (X) – log P (Y)],

или

H (X, Y) = H (X) + H (Y),

т.е. при объединении независимых систем их энтропии складываются.

Доказанное положение называется теоремой сложения энтропий.

Теорема сложения энтропии может быть легко обобщена на произвольное число независимых систем:

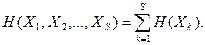
Если объединяемые системы зависимы, простое сложение энтропий уже неприменимо. В этом случае энтропия сложной системы меньше, чем сумма энтропий ее составных частей. Чтобы найти энтропию системы, составленной из зависимых элементов, нужно ввести новое понятие условной энтропии.

Дата добавления: 2014-12-27