Условная энтропия. Объединение зависимых систем

Пусть имеются две системы X и Y, в общем случае зависимые. Предположим, что система X приняла состояние x_i. Обозначим через P (y_i | x_i) условную вероятность того, что система Y примет состояние y_i при условии, что система X находится в состоянии x_i:

P (y_j | x_i) = P (Y ~ y_j | X ~ x_i).

Определим теперь условную энтропию системы Y при условии, что система X находится в состоянии x_i. Обозначим ее H (Y | x_i). По общему определению имеем:

(12.7)

или

Формулу (12.7) можно также записать в форме математического ожидания:

где знаком обозначено условное математическое ожидание величины, стоящей в скобках, при условии X ~ x_i.

Условная энтропия зависит от того, какое состояние x_i приняла система X; для одних состояний она будет больше, для других — меньше. Определим среднюю, или полную, энтропию системы Y с учетом того, что система может принимать разные состояния. Для этого нужно каждую условную энтропию (2.4.1) умножить на вероятность соответствующего состояния p_i и все такие произведения сложить. Обозначим полную условную энтропию H (Y | X):

или, пользуясь формулой (12.7),

Внося p_i под знак второй суммы, получим

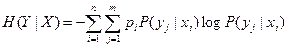
или

Но по теореме умножения вероятностей p_i P (y_j | x_i) = P_ij, следовательно,

(12.8)

Выражению где (2.4.2) тоже можно придать форму математического ожидания:

H (Y | X) = M [-log P (Y | X)]. (12.9)

Величина H (Y | X) характеризует степень неопределенности системы Y, остающуюся после того, как состояние системы X полностью определилось. Будем называть ее полной условной энтропией системы Y относительно X.

Пользуясь понятием условной энтропии, можно определить энтропию объединенной системы через энтропию ее составных частей.

Докажем следующую теорему:

Если две системы X и Y объединяются в одну, то энтропия объединенной системы равна энтропии одной из ее составных частей плюс условная энтропия второй части относительно первой:

H (X, Y) = H (X) + H (Y | X). (12.10)

Для доказательства запишем H (X, Y) в форме математического ожидания:

H (X, Y) = M [-log P (X, Y)].

По теореме умножения вероятностей

P (X, Y) = P (X) P (Y | X),

следовательно,

log P (X, Y) = log P (X) + log P (Y | X),

откуда

H (X, Y) = M [-log P (X)] + M [-log P (Y | X)],

или

H (X, Y) = H (X) + H (Y | X),

что и требовалось доказать.

В частном случае, когда системы X и Y независимы, H (Y | X) = H (Y), и мы получаем уже доказанную в предыдущем пункте теорему сложения энтропий:

H (X, Y) = H (X) + H (Y).

В общем случае

H (X, Y) £ H (X) + H (Y). (12.11)

Соотношение где (2.4.5) следует из того, что полная условная энтропия H (Y | X) не может превосходить безусловной:

H (Y | X) £ H (Y). (12.12)

Неравенство интуитивно представляется довольно очевидным: ясно, что степень неопределенности системы не может увеличиться оттого, что состояние какой-то другой системы стало известным.

Из соотношения следует, что энтропия сложной системы достигает максимума в крайнем случае, когда ее составные части независимы.

Рассмотрим другой крайний случай, когда состояние одной из систем (например X) полностью определяет собой состояние другой (Y). В этом случае H (Y | X) = 0, и формула дает

H (X, Y) = H (X).

Если состояние каждой из систем X, Y однозначно определяет состояние другой (или, как говорят, системы X и Y эквивалентны), то

H (X, Y) = H (X) = H (Y).

Теорему об энтропии сложной системы легко можно распространить на любое число объединяемых систем:

H (X₁, X₂,…, X_S) = H (X₁) + H (X₂ | X₁) + H (X₃ | X₁, X₂) + … + H (X_S | X₁, X₂,…, X_S-1),

где энтропия каждой последующей системы вычисляется при условии, что состояние всех предыдущих известно.

Дата добавления: 2014-12-27