Энтропия и информация для систем с непрерывным множеством состояний

До сих пор мы рассматривали физические системы, различные состояния которых x ₁, х ₂, …, x _n можно было все перечислить; вероятности этих состояний были какие-то отличные от нуля величины p ₁, р ₂, …, p _n. Такие системы аналогичны прерывным (дискретным) случайным величинам, принимающим значения x ₁, х ₂, …, x _n с вероятностями p ₁, р ₂, …, p _n. На практике часто встречаются физические системы другого типа, аналогичные непрерывным случайным величинам. Состояния таких систем нельзя перенумеровать: они непрерывно переходят одно в другое, причем каждое отдельное состояние имеет вероятность, равную нулю, а распределение вероятностей характеризуется некоторой плотностью. Такие системы, по аналогии с непрерывными случайными величинами, мы будем называть «непрерывными», в отличие от ранее рассмотренных, которые мы будем называть «дискретными». Наиболее простой пример непрерывной системы — это система, состояние которой описывается одной непрерывной случайной величиной X с плотностью распределения f(x). В более сложных случаях состояние системы описывается несколькими случайными величинами X₁, X₂,…, X_S с плотностью распределения f(x₁, x₂,…, x_S). Тогда ее можно рассматривать как объединение (X₁, X₂,…, X_S) простых систем X₁, X₂,…, X_S.

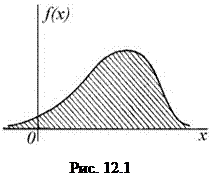Рассмотрим простую систему X, определяемую одной непрерывной случайной величиной X с плотностью распределения f(x) (рис. 12.1). Попытаемся распространить на эту систему введенное понятие энтропии.

Прежде всего отметим, что понятие «непрерывной системы», как и понятие «непрерывной случайной величины», является некоторой идеализацией. Например, когда мы считаем величину X — рост наугад взятого человека — непрерывной случайной величиной, мы отвлекаемся от того, что фактически никто не измеряет рост точнее, чем до 1 см, и что различить между собой два значения роста, разнящиеся, скажем, на 1 мм, практически невозможно. Тем не менее данную случайную величину естественно описывать как непрерывную, хотя можно было бы описать ее и как дискретную, считая совпадающими те значения роста, которые различаются менее чем на 1 см.

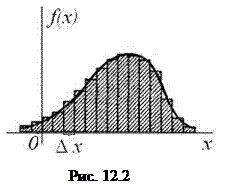Точно таким образом, установив предел точности измерений, т.е. некоторый отрезок Dx, в пределах которого состояния системы X практически неразличимы, можно приближенно свести непрерывную систему X к дискретной. Это равносильно замене плавной кривой f(x) ступенчатой, типа гистограммы (рис. 12.2); при этом каждый участок (разряд) длины Dx заменяется одной точкой - представителем. Площади прямоугольников изображают вероятности попадания в соответствующие разряды: f(x_i)Dx. Если условиться считать неразличимыми состояния системы, относящиеся к одному разряду, и объединить их все в одно состояние, то можно приближенно определить энтропию системы X, рассматриваемой с точностью до Dx:

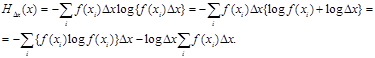(2.6.3)

При достаточно малом Dx:

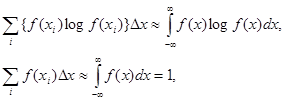
и формула (2.6.3) принимает вид

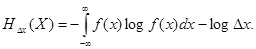(12.19)

Заметим, что в выражении (12.19) первый член получился совсем не зависящим от Dx — степени точности определения состояний системы. Зависит от Dx только второй член (- log Dx), который стремится к бесконечности при Dx ® 0. Это и естественно, так как чем точнее мы хотим задать состояние системы X, тем большую степень неопределенности мы должны устранить, и при неограниченном уменьшении Dx эта неопределенность растет тоже неограниченно.

Итак, задаваясь произвольно малым «участком нечувствительности» Dx наших измерительных приборов, с помощью которых определяется состояние физической системы X, можно найти энтропию H_Dx(X) по формуле (12.19), в которой второй член неограниченно растёт с уменьшением Dx. Сама энтропия H_Dx(X) отличается от этого неограниченно растущего члена на независимую от Dx величину

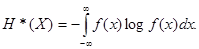
Эту величину можно назвать «приведенной энтропией» непрерывной системы X. Энтропия H_Dx(X) выражается через приведенную энтропию Н*(Х) формулой

H_Dx(X) = H*(X) – log Dx. (12.20)

Соотношение (12.20) можно истолковать следующим образом: от точности измерения Dx зависит только начало отсчета, при котором вычисляется энтропия.

В дальнейшем для упрощения записи мы будем опускать индекс Dx в обозначении энтропии и писать просто H(X); наличие в правой части всегда укажет, о какой точности идет речь.

Формуле (12.20) для энтропии можно придать более компактный вид, если, как мы это делали для прерывных величин, записать ее в виде математического ожидания функции. Прежде всего, перепишем (12.20) в виде

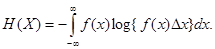
Это есть не что иное, как математическое ожидание функции – log {f (X) Dx} от случайной величины X с плотностью

f (x):

H (X) = M[- log {f (X)Dx}]. (12.21)

Аналогичную форму можно придать величине H*(X):

H*(X) = M[- log f (X)].

Перейдем к определению условной энтропии. Пусть имеются две непрерывные системы: X и Y. В общем случае эти системы зависимы. Обозначим f(x,у) плотность распределения для состояний объединенной системы (X, Y); f₁(x) — плотность распределения системы X; f₂(y) — плотность распределения системы Y; f (y | x), f (x | y) — условные плотности распределения.

Прежде всего, определим частную условную энтропию H (Y | x) т.е. энтропию системы Y при условии, что система X приняла определенное состояние х. Формула для нее будет аналогична, только вместо условных вероятностей P (y_i | x_i) будут стоять условные законы распределения f (y | x) и появится слагаемое log Dy:

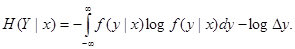
Перейдем теперь к полной (средней) условной энтропии H (Y | X); для этого нужно усреднить частную условную энтропию H (Y | x) по всем состояниям х с учетом их вероятностей, характеризуемых плотностью f₁(x):

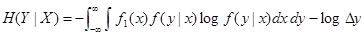
или, учитывая, что

f (x, y) = f₁ (x) f (y | x),

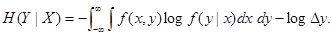
Иначе эта формула может быть записана в виде

H (Y | X) = M[- log f (Y | X)] – log Dy

или

H (Y | X) = M[- log {f (Y | X)Dy}]. (12.22)

Определив таким образом условную энтропию, покажем, как она применяется при определении энтропии объединенной системы.

Найдем сначала энтропию объединенной системы непосредственно. Если «участками нечувствительности» для систем X и Y будут Dx и Dy, то для объединенной системы (X, Y) роль их будет играть элементарный прямоугольник DxDy. Энтропия системы (X, Y) будет

H (X, Y) = M[- log {f (X, Y)DxDy}]. (12.23)

Так как

f (x, y) = f₁ (x) f (y | x),

то и

f (X, Y) = f₁ (X) f (Y | X). (12.24)

Подставим (2.6.9) в (2.6.8):

H (X, Y) = M[- log f₁ (X) – log f (Y | X) – log Dx – log Dy] =

= M[- log (f₁ (X) Dx)] + M[- log (f (Y | X) Dy)],

или

H (X, Y) = H (X) + H (Y | X),

т.е. теорема об энтропии сложной системы остается в силе и для непрерывных систем.

Если X и Y независимы, то энтропия объединенной системы равна сумме энтропий составных частей:

H (X, Y) = H (X) + H (Y).

Таким образом, мы распространили понятие энтропии на случай непрерывных систем. Аналогично может быть распространено и понятие информации. При этом неопределенность, связанная с наличием в выражении энтропии неограниченно возрастающего слагаемого, отпадает: при вычислении информации как разности двух энтропий, эти члены взаимно уничтожаются. Поэтому все виды информации, связанные с непрерывными величинами, оказываются не зависящими от «участка нечувствительности» Dx.

Выражение для полной взаимной информации, содержащейся в двух непрерывных системах X и Y, будет аналогично выражению, но с заменой вероятностей законами распределения, а сумм — интегралами:

,

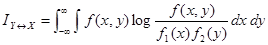или, применяя знак математического ожидания,

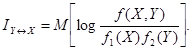
Полная взаимная информация I_{Y ® X}, как и в случае дискретных систем, есть неотрицательная величина, обращающаяся в нуль только тогда, когда системы X и Y независимы.

Дата добавления: 2014-12-27