Подготовка прибора к работе

Описание установки

ДИСК МАКСВЕЛЛА

Лабораторная работа М 9

Цель работы:

- найти величину модуля ускорения центра инерции диска Максвелла;

- определить значение моментов инерции диска и сменных накладок;

- научиться строить физическую и математическую модель изучаемого явления.

Приборы и принадлежности:

- установка FPM-03 для измерения времени движения диска, сменные накладки.

Рисунок 1 – Общий вид установки

Общий вид установки показан на рисунке 1. Основание (1) оснащено регулируемыми ножками (2), которые позволяют произвести выравнивание прибора. В основании закреплена колонка (3), к которой прикреплен неподвижный верхний кронштейн (4) и подвижный нижний кронштейн (5). На верхнем кронштейне находится электромагнит (6), первый фотоэлектрический датчик (7) и вороток (8) для закрепления и регулирования длины бифиллярной подвески маятника. Нижний кронштейн вместе с прикрепленным к нему вторым фотоэлектрическим датчиком (9) можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении.

Диск Максвелла (10) представляет собой закрепленный на оси диск, на который накладываются сменные накладки (11), что позволяет изменять момент инерции системы и ее массу.

Проверьте заземление прибора. Работа с прибором допускается только при наличии заземления. Прибор включается кнопкой "СЕТЬ". Измерение времени движения диска осуществляется следующим образом. Нажмите кнопку "СБРОС". Аккуратно (виток к витку) произведите намотку нитей бифиллярного подвеса до тех пор, пока диск не зафиксируется электромагнитом. Нажмите кнопку "ПУСК". На табло индикации времени прочитайте показание прибора.

Задания для самостоятельной работы.

1. Установите нижний кронштейн на расстоянии h₁ = 0,15 м от верхнего кронштейна (4). Проведите измерения времени движения диска 3-4 раза и найдите среднее время движения t₁.

2. Определите ускорение центра масс диска Максвелла по формуле:

,

где ∆h = 3∙10^{-3 м (Приложение 3).}

3. Повторите вычисление ускорения центра масс при значениях h = 0,15÷0,4 м с шагом 0,05 м и найти среднее значение ускорения (n – количество измерений)

4. Вычислите момент инерции диска Максвелла (J_с) относительно оси, проходящей через центр масс по формуле (Приложение 2):

,

где М – масса системы, r – радиус намотки, g = 9,8 м/с² – ускорение свободного падения.

5. Вычислите согласно Приложению 3 величины

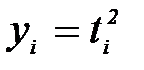
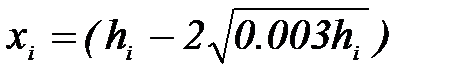
На координатную плоскость (Х, У) нанести экспериментальные точки. Согласно теории зависимость между величинами Х и У линейная: У = АХ. Проведите через начало координат и экспериментальные точки наилучшую с Вашей точки зрения прямую и найдите её угловой коэффициент А.

6. По формуле:

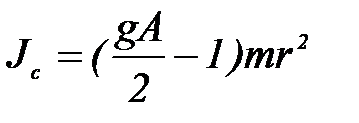
Опять найдите момент инерции J_c и сравните с результатами п. 4.

7. Согласно методу наименьших квадратов (Приложение 3) значение А находится по формуле:

Найдите это значение A и значение I_c и сравните с найденными ранее значениями.

8. Рассчитайте погрешность определения I_c по формуле:

,

учитывая для a_c лишь погрешности разброса. Погрешности массы и радиуса намотки принять равными: ∆m = 1 г; ∆r = 1 мм.

9. Вычислите теоретическое значение момента инерции системы по стандартным формулам и указанными на рабочем месте характеристикам системы и сравните с найденными экспериментальными значениями.

Приложение 1. Уравнение динамики твёрдого тела, вращающегося вокруг движущейся оси.

Пусть абсолютно твердое тело вращается вокруг некоторой оси О, которая неподвижна относительно некоторой инерциальной системы отсчета (ИСО). Тогда, как известно, основное уравнение динамики вращательного движения тела имеет вид

, (П-1.1)

где 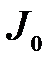– момент инерции тела относительно оси О:

,

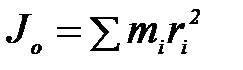где m_i – масса i- той частицы тела, r_i – расстояние от i -той частицы до оси О;

,

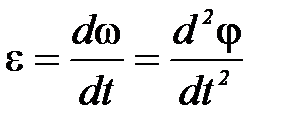где ε – угловое ускорение тела, 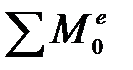– сумма моментов сил, действующих на тело, относительно оси О. Рассмотрим, как изменится уравнение (1), если ось О, относительно которой происходит вращение тела, сама движется с некоторым ускорением относительно ИСО, оставаясь параллельной себе, т.е. поступательно. Перейдем в неинерциальную систему отсчета, движущуюся поступательно относительно ИСО с тем же ускорением 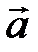, относительно которой ось неподвижна. В этой системе отсчета, наряду с силами, действующими на тело в ИСО, на каждую частицу тела будет действовать сила инерции, равная 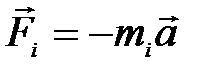и уравнение (1) примет вид

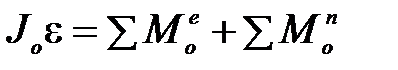
Напомним, что моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси. Пусть О – произвольная точка на оси О, 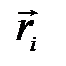– радиус-вектор частицы с массой m_i относительно точки О. Тогда момент силы инерции , действующей на 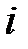-тую частицу относительно точки О, равен векторному произведению радиуса-вектора частицы и вектора силы инерции

.

Сумма этих моментов равна

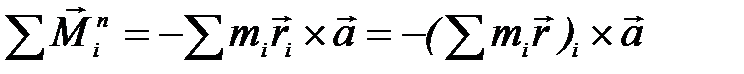. (П-1.2)

Здесь мы учли, что ускорение 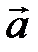одно и то же для всех точек, и вынесли его за знак суммы. Пусть – масса тела, С – его центр инерции, радиус-вектор которого равен

Тогда (2) можно переписать в виде

, (П-1.3)

где 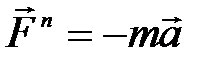– суммарная сила инерции, действующая на тело. Формула (3) показывает, что при вычислении суммы моментов сил инерции, действующих на отдельные частицы тела, можно считать, что к центру инерции тела приложена суммарная сила инерции ,и вычислить ее момент – он и будет равен искомой сумме моментов. Пусть теперь ось О проходит через центр инерции С (будем ее называть в таком случае осью С) и точка О совпадает с С. Тогда очевидно, =0 и =0, т.е. сумма моментов сил инерции, действующих на отдельные частицы тела, относительно центра инерции равна нулю, следовательно, и сумма моментов сил инерции относительно оси С: = 0. Это означает, что если ось вращения тела проходит через центр инерции С, то основное уравнение динамики вращательного движения тела имеет вид

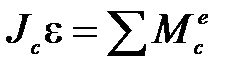, (П-1.4)

безотносительно к тому, покоится ли эта ось или движется ускоренно.

Приложение 2

Рисунок 2 – Силы, действующие на диск Максвелла

Диск Максвелла представляет собой достаточно массивный диск, насаженный на ось небольшого радиуса r. На ось симметрично наматываются две нити. Если диск отпустить, он начнет попеременно двигаться вверх-вниз, совершая своеобразные колебания – отсюда и его второе название: маятник Максвелла. С течением времени эти колебания затухают вследствие наличия сил сопротивления. Заметим, что по разным причинам, на анализе которых мы останавливаться не будем, с течением времени возбуждаются и обычные колебания в направлении, перпендикулярном оси диска. На рисунке 2 показан вид маятника сбоку и силы, действующие на него: 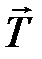– суммарная сила натяжения нитей и сила тяжести , приложенная к центру инерции. Силы сопротивления учитывать не будем, а нити будем считать вертикальными. Уравнение движения центра инерции в проекции на ось, направленную вниз, имеет вид

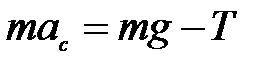, (П-2.1)

где a_c – ускорение центра инерции, m – масса маятника. Ось вращения маятника в данном случае ускоренно движется вниз. Согласно параграфу 5уравнение динамики вращательного движения имеет вид

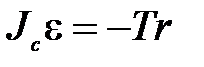, (П-2.2)

где r – радиус оси, J_c – момент инерции маятника относительно оси, проходящей через центр инерции. Рисунок соответствует движению маятника вниз, когда угловая скорость вращения направлена по часовой стрелке, и увеличивается, следовательно, в соответствии с обычным соглашением о знаках угловых величин: ω< 0, ε < 0. Между a_c и ε существует простая кинематическая связь, обусловленная нерастяжимостью нити и отсутствием проскальзывания нити по оси маятника. За время 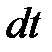маятника повернётся на угол и с оси намотки смотается участок нити длиной (знак минус поставлен с учетом отрицательности угловой скорости ). Таким образом, точка С опустится вниз на величину , а это означает, что скорость центра инерции при перемещении вниз будет равна

.

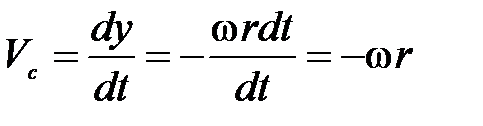Дифференцируя это соотношение по времени, получим

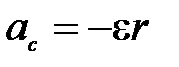. (П-2.3)

Подставляя (2.3) в (2.2), получим

,

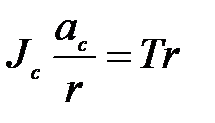откуда 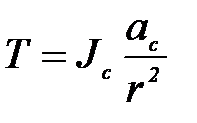. Подставляя в (2.1), получим

,

откуда

. (П-2.4)

Легко видеть, что формула (2.4) остается справедливой и при движении маятника вверх. Если нити абсолютно упруги, то по достижении центром инерции С наинизшей точки, его скорость изменит направление на противоположное и маятник начнет двигаться вверх замедленно, но с тем же ускорением (2.4) по величине.

Тот же результат можно получить из закона сохранения механической энергии, который справедлив в данном случае, поскольку мы пренебрегаем силами сопротивления (диссипативными силами). Считая потенциальную энергию центра инерции диска в наинизшем положении равной нулю, получаем значение потенциальной энергии центра инерции диска: mgh_c, где h_c – положение центра инерции диска над указанным нулевым уровнем в данный момент времени. Кинетическая энергия вращающегося тела, движущегося поступательно, равна . Тогда, согласно закону сохранения механической энергии, можно записать следующее соотношение:

,

где h_{c max} – наибольшее значение положения центра инерции над нулевым уровнем в момент начала движения. Дифференцируя это выражение по времени и учитывая, что 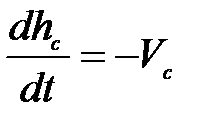(напомним, что мы считаем положительной скорость , если она направлена вниз, кроме того, поскольку h_c при этом убывает, то 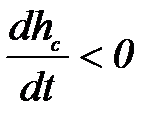) и , , получим

,

откуда опять получаем формулу (2.4), ибо V_c не равно тождественно нулю.

Приложение 3

На данной установке можно провести прямые измерения времени движения диска Максвелла на заданном расстоянии h, причем движение начинается из состояния покоя. Величины m и r также доступны непосредственному измерению, и мы будем считать их известными. Следовательно, в формулу (2.4) входят три неизвестных величины: g, J, a_c. Ускорение a_c, однако, легко может быть найдено по времени движения 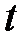и пройденному расстоянию h, т.к. в соответствии с (2.4) при сделанных предположениях a_c постоянно. Поскольку начальная скорость равна нулю, то в идеально функционирующей установке мы имели бы 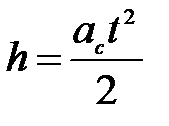и . К сожалению, из-за конструктивных особенностей установки отсчет времени начинается не сразу в момент начала движения, а тогда, когда система сместится на некоторое расстояние ∆ h, равное, по нашим оценкам, примерно 3 мм. На первый взгляд кажется, что если, например, высота, проходимая диском, составляет h = 30 см, то поскольку , т.е. примерно 1%, то погрешностью в определении ускорения по формуле можно вполне пренебречь. Однако на самом деле это не так. Начав движение из состояния покоя, система в конце участка ∆ h приобретает скорость . Тогда для оставшегося участка длиной (h – ∆ h) можно записать:

,

где t – время движения на этом участке, которое и измеряется на установке.

Тогда

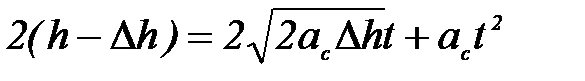
Решая это уравнение относительно , находим

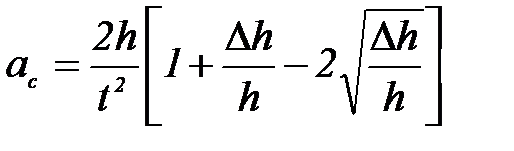. (П-3.1)

При указанных выше численных значениях имеем 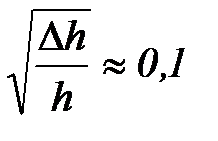и относительная погрешность в определении величины a_c по формуле 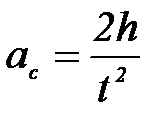составляет уже не 1%, а целых 20%, что слишком много, если учесть точность, с которой измеряется время движения и расстояние, проходимое диском. На уровне относительной погрешности 1% ускорение следует определять по формуле

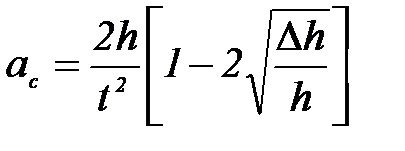, (П-3.2)

где мы пренебрегли величиной 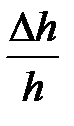по сравнению с единицей. Таким образом, в формулу

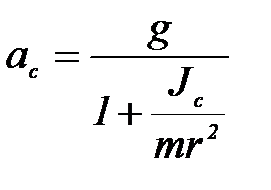(П-3.3)

входят две величины g и J_c, которые непосредственно не определяются. Конечно, значение ускорения свободного падения g хорошо известно из других опытов и составляет примерно . Тогда из формулы (3.3) можно определить момент инерции J_c и сравнить полученное значение с результатом, рассчитанным по теоретическим формулам.

Применим метод наименьших квадратов. Вначале линеаризируем исследуемую зависимость. Приравнивая правые части формул (3.2) и (3.3), получим

или

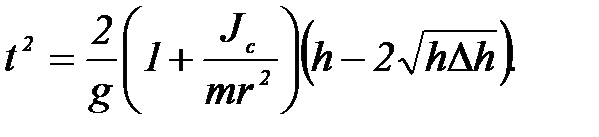(П-3.4)

Вводя обозначения

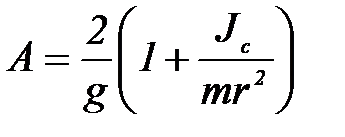и

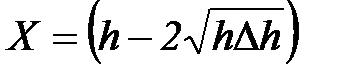
уравнение (3.4) можно переписать в виде линейного уравнения

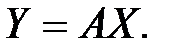(П-3.5)

Составляя сумму

, (П-3.6)

определим параметр А из условия минимума суммы (3.6):

Решая полученную систему линейных уравнений, находим значение параметра А:

(П-3.7)

Зная значение параметра А, можно определить значение момента инерции диска Максвелла и сменной накладки.

Дата добавления: 2014-12-27