Краткая теория работы

Рисунок 2

Рассмотрим конструкцию (см. рис. 2), состоящую из трёх сплошных цилиндров, показанную на рисунке. Пусть ρ – плотность материала цилиндров. Тогда массы цилиндров и масса системы равна

, , . (1)

Если систему поставить на две горизонтальные направляющие АВ и отклонить от положения равновесия, в котором центр масс С системы занимает наинизшее положение, то предоставленная самой себе система начнёт совершать колебания. Координата y_с центра масс системы (см. рисунок) определяется соотношением

(2)

Момент инерции системы относительно оси, проходящей через центр масс С находится по теореме Гюйгенса-Штейнера:

и 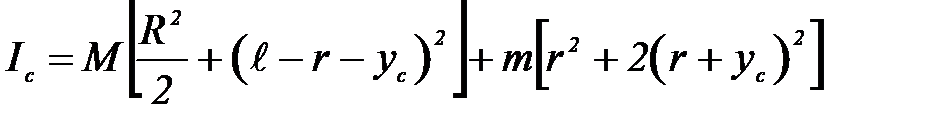(3)

Кинетическая энергия системы при качении по направляющим АВ находится по теореме Кёнига:

,

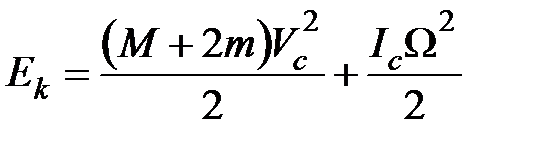где – угловая скорость вращения системы. Если качение происходит без проскальзывания, то скорость точки контакта системы с опорой равна нулю. Поэтому скорость центра масс связана с угловой скоростью соотношением 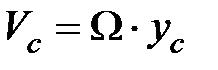. Таким образом,

(4)

При повороте на угол φ центр масс системы поднимается над низшим
положением, которое он занимает в положении равновесия на высоту

. Считая угол отклонения малым, имеем 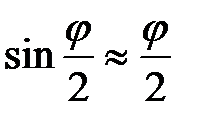и тогда, считая потенциальную энергию равной нулю в положении равновесия, получим для потенциальной энергии в отклонённом положении выражение:

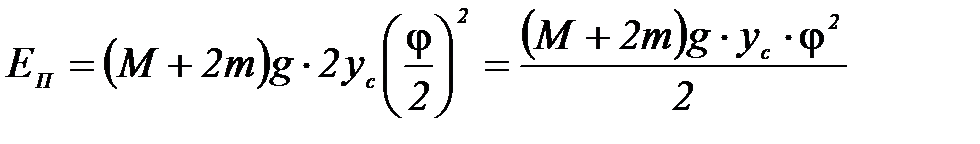(5)

Учитывая, что угловая скорость связана с углом отклонения соотношением 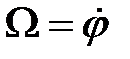, получим для полной механической энергии выражение:

(6)

Если пренебречь всеми силами трения, то полная механическая энергии системы сохраняется, т. е. энергия постоянна. Поэтому дифференцируя (6) по времени и отбрасывая тривиальное решение 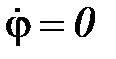, получим дифференциальное уравнение гармонических колебаний:

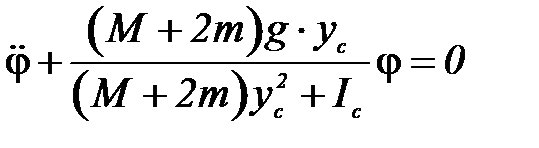(7)

Циклическая частота ω и период T этих колебаний равны соответственно

, .

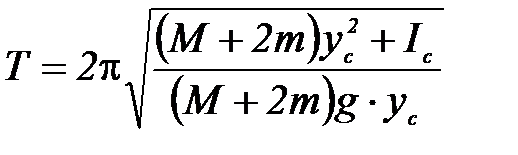Реально на рассматриваемую конструкцию при колебаниях действуют две диссипативные силы: сила вязкого трения о воздух и сила трения качения (см. рис. 3).

Влияние силы вязкого трения сказывается тем меньше, чем больше масса конструкции и меньше её угловая скорость , т. е. угловая амплитуда колебаний. Для данной установки, как показывают расчёты, влиянием силы вязкого трения можно пренебречь. Трение качения возникает вследствие того, что при качении деформации опоры и катящегося тела не вполне симметричны и упруги (на рисунке показана только де формация опоры в сильно преувеличенном виде). При этом сила нормальной реакции N = mg оказывается вынесенной вперёд относительно центра цилиндра С на отрезок, длина которого S называется коэффициентомтре­ния качения. Смысл этого названия состоит в следующем. Сила трения (F_тр), направленная против скорости 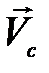, момент которой относительно оси, проходящей через центр масс,

Рисунок 3

практически равен F_тр ∙R (деформа­ция цилиндра реально очень мала!), увеличивает угловую скорость вращения диска, но одновременно уменьшает скорость центра масс. Если, однако, что обычно подразумевается, проскальзывание при качении отсутствует, то , так что тормозит вращение диска именно сила реакции опоры (N), момент которой относительно оси, проходящей через центр масс, равен NS. Опыт показывает, что сила трения качения обычно очень мала, т. е. можно считать, что

F_ТРR ≈NS = mgS,

так что

В, принципе,для сохранения аналогии с силой сухого трения скольжения можно было бы величину 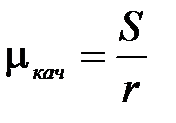называть коэффициентом трения качения, тогда 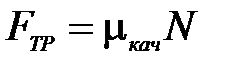,однако как сказано выше, исторически сложилось так, что коэффициентом трения качения называется величина S. Поэтому при наличии трения качения вместо уравнения (4) мы имеем следующее уравнение

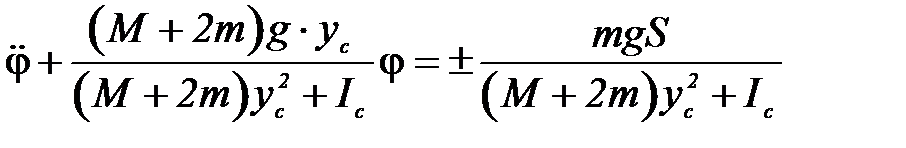
где знак 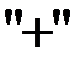соответствует движению центра масс направо (поворот системы по часовой стрелке) и знак «минус» соответствует повороту против часовой стрелки. Поскольку постоянная правая часть в дифференциальном уравнении не изменяет величину ω, то она по-прежнему выражается формулой (5). Колебания при этом, однако, затухают, и если обозначить φ_о начальный угол отклонения ( 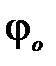> 0, т. е. система при t = 0 повёрнута против часовой стрелки), то спустя период Т отклонение составит

,

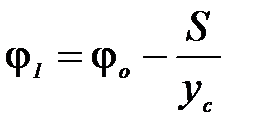а спустя m периодов:

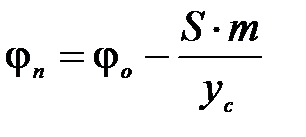(8)

Измеряя, таким образом, 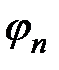,можно определить коэффициент трения качения S. Зависимость 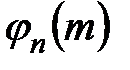линейная, поэтому лучшим способом определения S является метод наименьших квадратов, который в данном случае даёт

(9)

При этом подразумевается, конечно, что угол измеряется в радианах (по шкале прибора он отсчитывается в градусах: 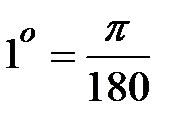рад)

Задания для самостоятельной работы.

1. Используя указанные на рабочем месте значения размеров системы и плотности материала, найдите по формуле (1) массы М и m, а также значение y_c и I_c по формуле (2) и (3).

2. Аккуратно установите систему так, чтобы стрелка указывала на угол 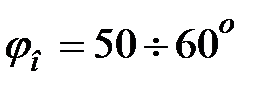и отпустите без толчка. Измерьте время, в течение которого совершается 20 колебаний, а затем, продолжая наблюдать колебания, измерьте время следующих 20 колебаний и т. д.

3. Найдите экспериментально период колебаний для первых 20 колебаний, следующих 20 колебаний, когда угловая амплитуда уменьшится и т. д. Сделайте вывод о том, с какой относительной погрешностью выполняется теоретический вывод о независимости периода от угловой амплитуды в предположении её малости. По формуле (3) рассчитайте теоретическое значение периода.

4. Наблюдая колебания, определите примерное количество колебаний, которое совершает система, пока угловая амплитуда уменьшится до 10^о. Разделите это число на 5 и округлите до кратного 10 значения. Обозначим полученное значение n. Вновь запустив колебания без начальной скорости при начальной угловой амплитуде 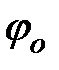в указанных пределах.

5. Измерьте угловую амплитуду через n₁ = n, через n₂ = 2n, через n_i = i∙n колебаний (угловая амплитуда измеряется по шкале в градусах, но переводится в радианы).

6. На координатной плоскости, откладывая по горизонтали n_i, а по вертикали , нанесите экспериментальные точки. Теория предсказывает, что все точки должны лежать на прямой. По формуле, вытекающей из (8) и имеющей вид

,

Найдите коэффициент трения качения для всех экспериментальных точек

и усредните результат.

7. Повторите определение коэффициента трения качения по МНК. По формуле (9) имеем

На указанной координатной плоскости проведите наилучшую прямую и визуально оцените соответствие экспериментальных данных теоретической модели.

8. По формуле найдите начальную потенциальную энергию системы пр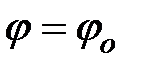и и через n периодов. Рассчитайте среднее умень­шение энергии за один период и относительное уменьшение за период в %.

9. Снимите конструкцию с основания и с помощью преподавателя замените направляющие АВ на направляющие из другого материала. Повторите измерения п. п. 1 4 для другой пары направляющих.

10.*Поскольку относительное уменьшение энергии за период мало, то максимальную угловую скорость системы можно рассчитать по формуле, вытекающей из формул (4) и (5)

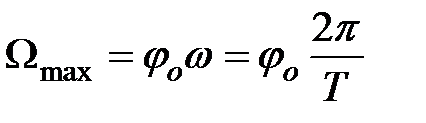
Вычислите это значение. Используя табличное значение для коэффициента вязкости воздуха 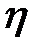, оцените максимальный момент сил вязкого трения о воздух и сравните с величиной (M + 2m)gS, определяющей момент сил трения качения.

11.*Установка допускает магнитное крепление дополнительного груза масс сой m_o и радиусом r_{o (}на рисунке заштрихован). Разработайте теорию и повторите выполнение всех заданий для новой системы.

Контрольные вопросы.

1. Получите выражение для момента инерции системы для оси, проходящей через точку касания с направляющими.

2. Вычислите период малых колебаний шарика внутри полусферы.

3. Оцените, сколько колебаний совершает система до остановки. Сколько вре­мени это займёт? Начальную угловую амплитуду задайте самостоятельно.

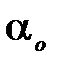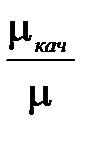4. Осторожно наклонив основание, можно оценить, при каком угле наклона начнётся скольжение конструкции по основанию. Коэффициент трения скольжения при этом находится из соотношения . Оцените отношение , где .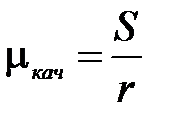

Дата добавления: 2014-12-27