
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методика измерений
|
|
|
|
Описание любой экспериментальной ситуации, в том числе и колебаний маятника, дается теоретической моделью. При разработке модели, естественно, учитывают только наиболее существенные для данной ситуации эффекты и пренебрегают влиянием многих, реально имеющих место факторов. Ответить на вопрос: насколько хорошо теоретическая модель описывает эксперименталь-ную ситуацию, можно только сопоставляя предсказания теории с эксперимен-тальными данными.
Наблюдения за колебаниями математического и оборотного маятников на данной установке показывают, что за время 20 - 30 периодов амплитуда их колебаний заметно не уменьшается. Это означает, что диссипативными силами, т.е. силами трения, сопротивления воздуха и т. д., приводящими к затуханию колебаний, в данном случае можно пренебречь. Кроме того, можно предположить, что колебания математического и оборотного маятников являются малыми. При этих условиях теория дает следующее выражение для периода колебаний оборотного маятника (см. Приложение 1):
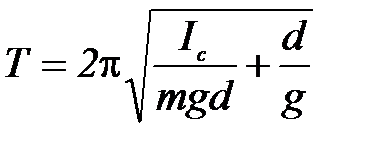 , (1)
, (1)
где Iс – момент инерции маятника относительно оси, проходящей через его центр масс; m – масса маятника; g – ускорение свободного падения; d – расстояние от оси качаний до центра масс маятника.
В случае математического маятника формулa (1) принимает вид:
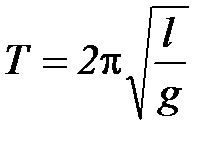 , (2)
, (2)
где l – длина математического маятника.
Формулы (1) и (2) являются основными для данной работы, так как позволяют определить ускорение свободного падения g по измеренным значениям T, d, l, m. Однако они справедливы только в том случае, если колебания маятников являются малыми.
Внимание: Перед началом измерений необходимо определить диапазон амплитуд, в пределах которых колебания можно считать малыми. Поскольку данная установка не позволяет измерять углы отклонения маятника от положения равновесия, их нельзя использовать в качестве критерия малости колебаний. Реализация этого критерия может быть осуществлена следующим образом.
Отклоните математический или оборотный маятник на угол φ1 ~ 10о и измерьте период его колебаний Т1 в соответствии с процедурой, описанной выше. Затем, уменьшив начальное отклонение маятника в 1,5-2 раза, опять определите период его колебаний Т2. Относительная погрешность измерения времени на данной установке
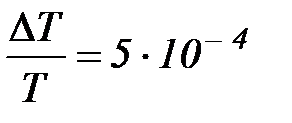 .
.
С другой стороны, период колебаний маятника не превышает 2 с. Поэтому если |T1 – T2| ≤ 0,001, то в пределах точности измерений T1 = T2, и для дальнейших измерений можно выбирать любое начальное отклонение маятника, меньшее φ1. Если же |T1 – T 2| > 0,001, то необходимо еще уменьшить начальное отклонение маятника, сравнить измеренный при этом период колебаний с Т2 и т. д.
Задание 1. Определение ускорения свободного падения с помощью математического маятника.
1. Установив любое значение длины математического маятника l (расстояние от точки подвеса – до черты, нанесенной на шарик) в интервале от 35 до 40 см, измерьте период его колебаний Т. Затем, увеличив l на несколько сантиметров, опять измерьте Т и т. д. Шаг измерения l выберите таким образом, чтобы измерения Т были проведены не менее чем при 6 ÷ 8 значениях l. В результате получится набор значений периодов колебаний Ti, соответствующих длинам маятника li, где i – номер опыта. При каждом значении l измерения периода проводите 3 раза и усредняйте полученные значения.
2. Данные занесите в таблицу:
Таблица
| № п/п | 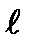 , см , см
| Т1, сек | Т2, сек | Т3, сек | 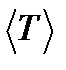 , сек , сек
| 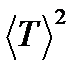 , сек , сек
|
3. Постройте график зависимости 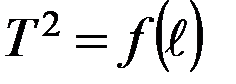
По данным из таблицы отложите по оси абсцисс значения 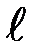 , а по оси ординат – значения переменной у = Т2 и нанесите на график экспериментальные точки. Проведите через них наилучшую прямую (т. е. такую, чтобы отклонение каждой экспериментальной точки от данной прямой было примерно одинаковым). Проведите эту прямую вначале на глаз, а затем используя метод наименьших квадратов.
, а по оси ординат – значения переменной у = Т2 и нанесите на график экспериментальные точки. Проведите через них наилучшую прямую (т. е. такую, чтобы отклонение каждой экспериментальной точки от данной прямой было примерно одинаковым). Проведите эту прямую вначале на глаз, а затем используя метод наименьших квадратов.
Т2, с С
Е Д
0 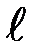 , см
, см
4. Значения Т и 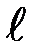 для математического маятника связаны между собой зависимостью (2), поэтому
для математического маятника связаны между собой зависимостью (2), поэтому
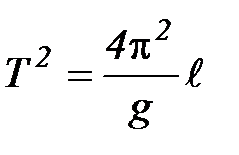 или Y = Al (3)
или Y = Al (3)
где 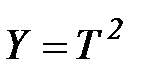 ,
, 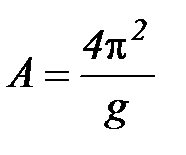 . Следовательно, согласно теории прямая на координатной плоскости (Y, X) должна проходить через начало координат. Опыт, однако, показывает, что наилучшая прямая не проходит через начало координат (подумайте о возможных причинах этого!). Поэтому по рисунку определяют угловой коэффициент прямой как отклонение длин отрезков СД и ЕД:
. Следовательно, согласно теории прямая на координатной плоскости (Y, X) должна проходить через начало координат. Опыт, однако, показывает, что наилучшая прямая не проходит через начало координат (подумайте о возможных причинах этого!). Поэтому по рисунку определяют угловой коэффициент прямой как отклонение длин отрезков СД и ЕД:  . Тогда
. Тогда
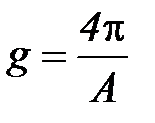
Очевидно, из графика: 
Из уравнения (3): 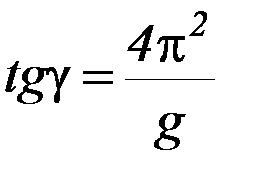
Следовательно: 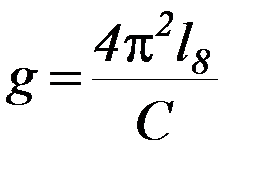 (4)
(4)
Определите ускорение свободного падения g по формуле (4).
5. Рассчитайте погрешность измерения ускорения свободного падения g по формуле:
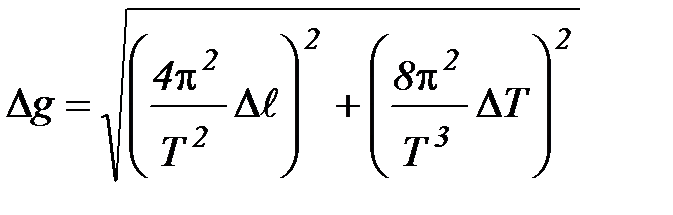 ,
,
где 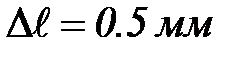 ;
; 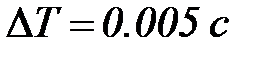 .
.
Задание 2. Определение ускорения свободного падения с помощью оборотного маятника и момента инерции Jc оборотного маятника
1. Зафиксируйте чечевицы на стержне оборотного маятника таким образом, чтобы одна из них находилась вблизи конца стержня, а другая – вблизи его середины (см. рисунок 2).
| C |
| 1 2 |
| d1d2 |
Рисунок 2 – Оборотный маятник
Одну из опорных призм зафиксируйте вблизи свободного конца стержня, а вторую – между чечевицами, причем опорные проемы должны быть обращены друг к другу.
2. Определите положение центра масс (т. С) оборотного маятника, уравновешивая его на дополнительной опорной призме, расположенной на лабораторном столе. Если оказалось, что центр массы маятника находится между опорными призмами, значит, оборотный маятник собран правильно.
Чтобы точность определения ускорения свободного падения была достаточно высокой, необходимо, чтобы расстояния d1 и d2 от центра масс (т. С) до опорных призм, удовлетворяли условию:
1,5d2 < d1 < 3d2 (5)
Используя нарезки на стержне оборотного маятника, установите опорную призму, находящуюся между чечевицами на расстоянии d2 = 10 – 15 см от центра масс маятника. Вторую опорную призму зафиксируйте на таком расстоянии d1 от центра масс маятника, которое удовлетворяет неравенству (5).
3. Установив маятник на вкладыши верхнего кронштейна опорной призмой, находящейся вблизи свободного конца стержня на расстоянии d1 от центра масс маятника, измерьте период его колебаний Т1. Затем переверните маятник и, установив его на вкладыши верхнего кронштейна опорной призмой, находящейся между чечевицами, измерьте период его колебаний Т2.
4. Используя измеренные значения d1, d2, T1, Т2, решите систему уравнений (6) и (7) и рассчитайте ускорение свободного падения g и момент инерциимаятника Jc относительно оси, проходящей через его центр масс.
Теория даёт следующие уравнения для нахождения периода оборотного маятника:
 (6)
(6)
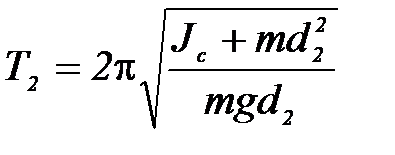 , (7)
, (7)
где m – масса всего маятника; Jc – момент инерции маятника относительно оси, проходящей через т. С (центр масс маятника)
5. Не изменяя положения чечевиц, повторите измерения при других значениях d1, d2 удовлетворяющих условию (5), и результаты Jc и g, полученные в пунктах 4) и 5) усредните.
6. Рассчитайте относительную погрешность определения ускорения свободного падения и момента инерции оборотного маятника (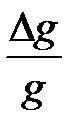 ,
, 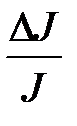 ).
).
В силу сложности математического выражения для определения данной погрешности можно воспользоваться упрощённым вариантом расчёта. Для этого относительные погрешности прямым образом определяемых величин (M, d, T) принять равными: 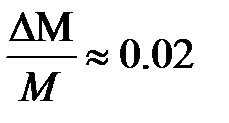 ;
; 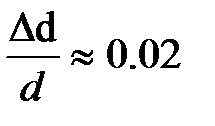 . (В данной работе период рассматриваем как прямым образом измеренную величину). Относительной погрешностью измерения периода в силу малости можно пренебречь. Рассчитайте относительную погрешность определениямомента инерции и коэффициента упругих сил кручения как сумму относительных погрешностей прямым образом определяемых величин.
. (В данной работе период рассматриваем как прямым образом измеренную величину). Относительной погрешностью измерения периода в силу малости можно пренебречь. Рассчитайте относительную погрешность определениямомента инерции и коэффициента упругих сил кручения как сумму относительных погрешностей прямым образом определяемых величин.
Приложение. Теория малых колебаний физического маятника.
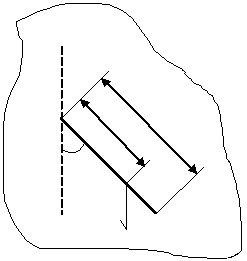
| mg |
| φ |
| o |
| c |
| O’ |
| Рисунок 3 3. Приведенная длина |
Движение маятника описывается основным уравнением динамики вращательного движения вокруг неподвижной оси:
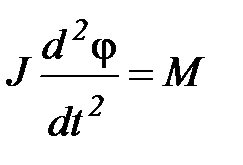 ,
,
где J – момент инерции маятника относительно оси вращения, φ – угол отклонения маятника от положения равновесия, М – суммарный момент внешних сил, действующих на маятник относительно оси вращения.
В экспериментальных установках обычно моменты силы трения в оси и силы сопротивления воздуха пренебрежимо малы. Поэтому Мс = – mgd sinφ, где
d = │ОС│ – расстояние от оси качания до центра масс, m – масса маятника,
g – ускорение свободного падения, а знак " – " указывает на то, что момент силы тяжести стремится возвратить маятник в положение равновесия. Таким образом, уравнение движения маятника имеет вид:
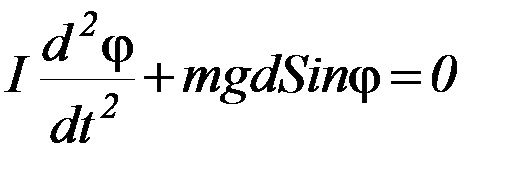 (П-1)
(П-1)
В случае малых отклонений маятника от положения равновесия (т.е. φ << 1) можно положить sin φ ≈ φ. Тогда уравнение (П-1) примет вид:
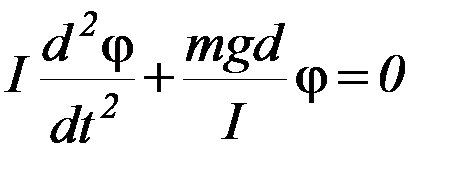 (П-2)
(П-2)
Легко убедиться, что решением этого уравнения является функция
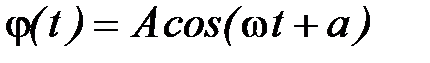
где 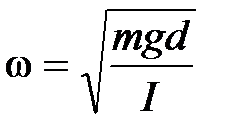 , а А и α – произвольные постоянные, т.е. величина φ(t) совершает гармонические колебания с циклической частотой ω. Амплитуда А и начальная фаза колебаний α зависят от способа возбуждений колебаний, т.е. определяются значениями φ и
, а А и α – произвольные постоянные, т.е. величина φ(t) совершает гармонические колебания с циклической частотой ω. Амплитуда А и начальная фаза колебаний α зависят от способа возбуждений колебаний, т.е. определяются значениями φ и 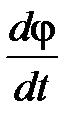 в момент времени t = 0. Частота колебаний ω определяется только параметрами маятника m, J, d.
в момент времени t = 0. Частота колебаний ω определяется только параметрами маятника m, J, d.
Таким образом, при малых углах отклонения от положения равновесия колебания физического маятника являются гармоническими с периодом
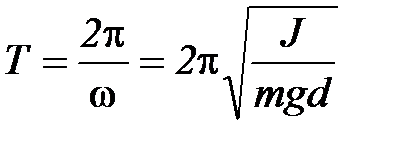 , (П-3)
, (П-3)
причем период колебаний не зависит ни от начальной фазы, ни от амплитуды колебаний, а определяется только параметрами маятника.
Согласно теореме Гюйгенса-Штейнера момент инерции маятника J относительно оси вращения можно представить в виде:
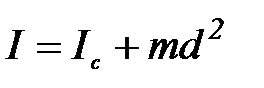 , (П-4)
, (П-4)
где Jc – момент инерции маятника относительно оси, проходящей через его центр масс.
Используя (П-4), формулу (П-3) можно переписать следующим образом:
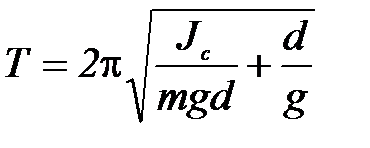 (П-5)
(П-5)
Частным случаем физического маятника является математический маятник. Это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке – центре масс маятника С. Для математического маятника длиной 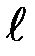 имеем: d =
имеем: d = 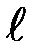 . Jc = 0. Тогда формула (П-5) принимает вид:
. Jc = 0. Тогда формула (П-5) принимает вид:
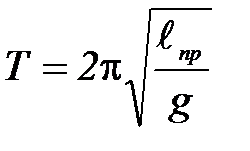 (П-6)
(П-6)
Сравнение формул (П-5) и (П-6) показывает, что период колебаний физического маятника равняется периоду колебаний математического маятника длиной
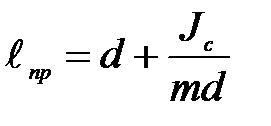 (П-7)
(П-7)
Величину lпр называют приведённой длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Как следует из (П-7), приведенная длина физического маятника больше, чем расстояние от оси качания до центра масс маятника. Точка О, находящаяся от точки 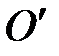 на расстоянии lпр вдоль прямой, соединяющей точку подвеса с центром масс, называется центром качаний. Если маятник подвесить в точке
на расстоянии lпр вдоль прямой, соединяющей точку подвеса с центром масс, называется центром качаний. Если маятник подвесить в точке 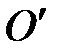 , то период его колебаний будет тот же, что и при подвешивании в точке О. Действительно, при подвешивании маятника в точке
, то период его колебаний будет тот же, что и при подвешивании в точке О. Действительно, при подвешивании маятника в точке 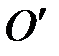 , из (П-5) получаем следующее выражение для периода колебаний:
, из (П-5) получаем следующее выражение для периода колебаний:
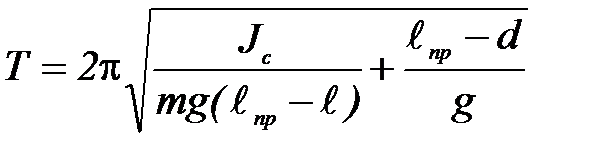 (П-8)
(П-8)
Из (П-7) имеем: 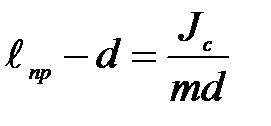
Тогда 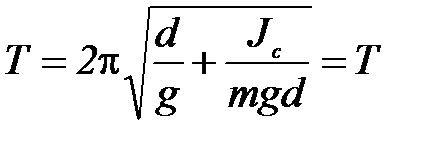
Таким образом, период колебаний физического маятника не изменяется при перемещении оси качаний в центр качаний.
Контрольные вопросы.
1. Какие предположения используются при построении теоретической модели колебаний маятника? Как их проверить?
2. Дайте определение понятию «физический маятник». Приведите примеры.
3. Дайте определение понятию «математический маятник»?
4. Сформулируйте определение длины физического маятника.
5. В чем состоит метод измерения ускорения свободного падения с помощью математического маятника?
6. Как повысить точность измерения ускорения свободного падения с помощью оборотного маятника?
7. В чем состоит метод оборотного маятника определения ускорения свободного падения?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1678; Нарушение авторских прав?; Мы поможем в написании вашей работы!