Цепи со взаимной индуктивностью

Если изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, считают, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции.

На рис. 3.22, а схематично представлено распределение магнитных потоков у двух близко расположенных индуктивных катушек. У магнитного потока первой катушки Ф ₁ часть потока Ф ₁₁ связана (сцеплена) с витками этой катушки, а часть потока Ф₁₂ пронизывает вторую катушку, т.е. Ф ₁ = Ф ₁₁ + Ф ₁₂.

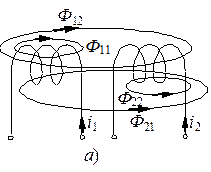
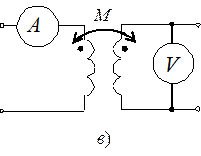
Рис. 3.22. Цепь со взаимной индуктивностью: – схема магнитных потоков; б –разметка концов индуктивно связанных катушек; в – определение взаимной индуктивности

У второй катушки Ф ₂ = Ф ₂₂ + Ф ₂₁. В итоге потокосцепление первой катушки w ₁ (Ф ₁₁ + Ф ₁₂ + Ф ₂₁) = Y ₁₁ + Y ₁₂ + Y ₂₁ = Y ₁ + Y ₂₁. Аналогично потокосцепление у второй катушки

w ₂ (Ф ₂ + Ф ₁₂) = Y ₂ + Y ₁₂.

Часть потока от соседней катушки может оказаться со знаком плюс, когда потоки направлены согласно, или со знаком минус, когда потоки направлены встречно.

Потокосцепление Y ₂₁ пропорционально току i ₂, а Y ₁₂ – току i ₁, т.е. Y ₂₁ = w ₁ Ф ₂₁ = M ₂₁ i ₂ = Mi ₂, Y ₁₂ = w ₁₂ Ф ₁₂ = M ₁₂ i ₁ = Mi ₁.

Коэффициент пропорциональности М (Гн) называют взаимной индуктивностью. Доказывается, что М = М ₂₁ = М ₁₂.

При изменении токов в катушках наводятся ЭДС

Их называют соответственно e_L – ЭДС самоиндукции, e_M – ЭДС взаимоиндукции.

Для оценки степени индуктивной связи вводят коэффициент связи 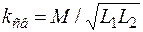. Коэффициент связи всегда меньше единицы.

Магнитная энергия двух индуктивно связанных катушек

.

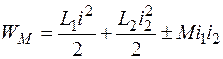Чтобы знать, согласно или встречно включены катушки, делают разметку их концов. На схемах начала обмоток обозначают точкой или звездочкой (рис. 3.30, б). Выполнить разметку концов и определить взаимную индуктивность можно экспериментально. Для этого включают обе катушки последовательно под напряжение U.

Если катушки включены согласно, то уравнение напряжений будет иметь вид ,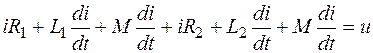

или в комплексном виде

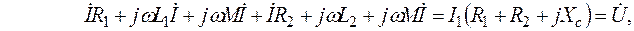
где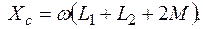

Если катушки включены встречно, то

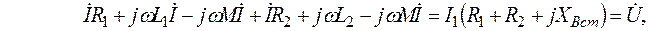где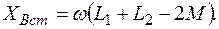

Как видно при встречном включении полное сопротивление цепи меньше и при неизменном напряжении ток будет больше, чем при согласном включении. Это является критерием для разметки концов катушек.

Для определения значения взаимной индуктивности определим 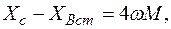или .

Можно определить взаимную индуктивность и другим способом (рис. 3.22, в).

На разомкнутых концах второй катушки измеряется напряжение, равное ЭДС взаимоиндукции и пропорциональное току в первой катушке 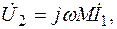тогда М = U ₂/ ωI ₁.

При расчете разветвленных цепей с взаимными индуктивностями составляют уравнения по законам Кирхгофа. Можно применять метод контурных токов, но нельзя применять метод узловых потенциалов, так как ток в некоторых ветвях будет зависеть не только от ЭДС и потенциалов узлов, но и от токов в ветвях. Для примера составим уравнения для схемы, представленной на рис. 3.23,

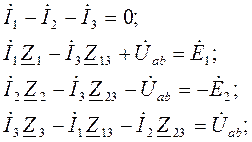
где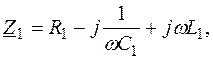

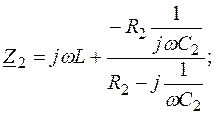
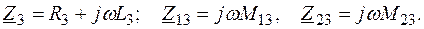
Слагаемые 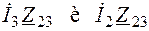взяты со знаком минус потому, что потоки в катушках L ₂ и L ₃ направлены встречно (ток I ₃ входит в начало катушки L ₃, а ток L ₂ – в конец L ₂).

Чтобы упростить составление уравнений разветвленной цепи (в том числе применить любой метод расчета, например метод узловых потенциалов) применяют так называемое «развязывание» магнитно-связанных цепей.

Если две ветви, имеющие взаимную индуктивность M, подключены к узлу 3 (рис. 3.24, а), то, заменив эту схему на схему, представленную на рис. 3.24, б, получим полностью эквивалентную схему, но не содержащую индуктивных связей.

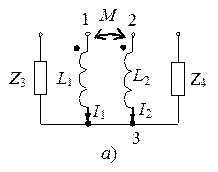
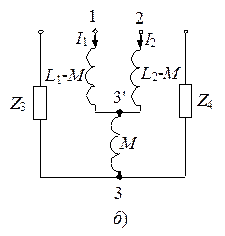
Рис. 3.24. «Развязка» индуктивно связанных цепей:

а – исходная схема; б – преобразованная схема цепи

Действительно, для первой схемы с индуктивными связями

,

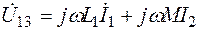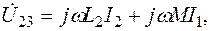
для второй схемы без индуктивной связи

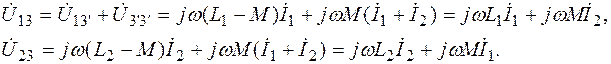Необходимо следить за тем, чтобы токи I ₁ и I ₂ были направлены к узлу 3. Если при этом окажется, что катушки включены встречно, то знаки, стоящие перед М, меняются на противоположные

(т.е. будут L ₁ + M, L ₂ + M и – M).

П р и м е р 3.10. Определить входное сопротивление цепи, показанной на рис. 3.25, а.

Р е ш е н и е. Применив «развязывание», определим (рис. 3.25, б)

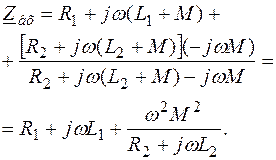
Дата добавления: 2014-12-27