Последовательного колебательного контура

Избирательные свойства

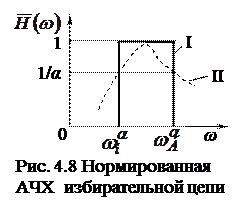Особенностью последовательного колебательного контура является зависимость амплитуды реакции контура на гармоническое воздействие от частоты. На резонансной частоте и в узком диапазоне частот около нее амплитуда отклика достигает наибольшего значения, а на частотах, значительно отличающихся от резонансной, амплитуда отклика во много раз меньше максимального значения. Если на вход такого контура подать сумму гармонических колебаний различных частот, имеющих одинаковые амплитуды, то на выходе можно обнаружить, что амплитуда колебаний, частота которых близка к резонансной, значительно превышает амплитуду колебаний, частота которых отличается от резонансной. Контур как бы «пропускает» колебания одних частот и «не пропускает» колебания других частот. Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.

В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона. Нормированная АЧХ идеальной избирательной цепи должна иметь прямоугольную форму (кривая I на рис. 4.8). АЧХ реальных избирательных цепей, в том числе и АЧХ последовательного колебательного контура (кривая II на рис. 4.9), отличаются от характеристик идеальной избирательной цепи отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот. Очевидно, избирательные свойства реальных цепей тем выше, чем ближе к прямоугольной форма их нормированной АЧХ.

В соответствии с уравнением (4.19) модуль тока I в ПСК равен

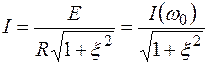. (4.20)

На практике также используют частотную зависимость модуля тока ПСК, называемую входной резонансной характеристикой ПСК

(рис. 4.9) .

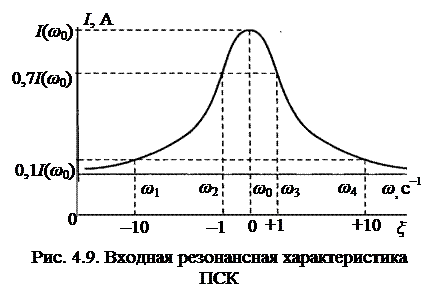Графики частотной зависимости модуля тока (рис. 4.9) и графики АЧХ входной проводимости ПСК (рис. 4.7) полностью аналогичны. Они позволяют определить полосу пропускания и коэффициент прямоугольности ПСК.

На уровне 0,7 от максимального значения тока определяется полоса пропускания ПСК шириной Δω _п = ω ₃ – ω ₂, а на уровне 0,1 от I (ω ₀) – полоса мешания ПСК шириной Δω _м = ω ₄ – ω ₁.

Отношение 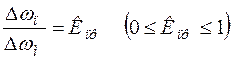называют коэффициентом прямоугольности ПСК, так как он характеризует степень приближения резонансной характеристики ПСК к идеальной прямоугольной форме с К_пр =1.

Согласно уравнению (4.20), для полосы пропускания

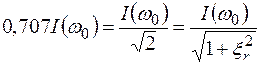при ξ_r = ±1.

Так как полоса пропускания Δω _п равна двойному значению абсолютной расстройки Δω = ω – ω ₀, т.е. 2 Δω = Δω _п, получим

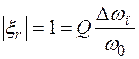, т.е. .

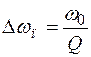Аналогично для полосы мешания

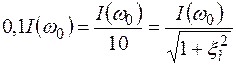при ξ_м = ±10.

Тогда из (4.29) с учетом, что 2 Δω = Δω _м, получим ,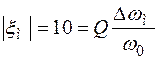

т.е. .

Следовательно, , т.е. для любого ПСК всегда

К_пр = 0,1.

Дата добавления: 2014-12-27