Дисперсия

Разброс выборки

Разброс – это разность между максимальной и минимальной величинами данного конкретного вариационного ряда (иногда эту величину называют размахом) и обозначают буквой R.

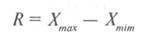
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R и наоборот.

Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки:

При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того, чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям.

Рассмотрим еще одну очень важную числовую характеристику выборки, называемую дисперсией. Дисперсия - это среднее арифметическое квадратов отклонений значений переменной от её среднего значения.

где n – объем выборки

∑ – индекс суммирования

X – среднее, вычисляемое по формуле (4.1).

Вычислим дисперсию следующего ряда:

2 4 6 8 10

Прежде всего, найдем среднее арифметическое ряда Оно равно X = 6.

Рассмотрим величины: (Xi – X) для каждого элемента ряда. Иными словами, из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду.

Обозначим полученную совокупность разностей как множество Т.

Тогда Т есть:

Т = (2 – 6 = -4; 4 – 6 = -2; 6 – 6 = 0; 8 – 6 = 2; 10 – 6 = 4).

Так образуется новый ряд чисел. Его особенность в том, что при сложении этих чисел обязательно получится ноль. Проверим: (-4) + (-2) + 0 + 2 + 4 = 0.

Отметим, что сумма такого ряда ∑ (Хi – `X) всегда будет равна нулю.

Для того, чтобы избавиться от нуля, каждое значение разности (Хi – `X) возводят в квадрат, все их суммируют и затем делят на число элементов, т.е. применяют формулу 4.4.

В нашем примере получится следующее:

Таблица

числовой ряд	Х-Х	(Х-Х)2
	-4 -2
Ср.Х

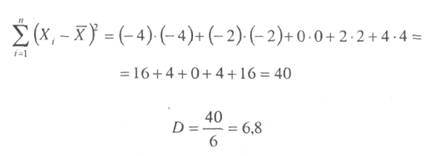
Это и есть искомая дисперсия.

Общий алгоритм вычисления дисперсии для одной выборки следующий:

1. Вычисляется среднее по выборке.

2. Для каждого элемента выборки вычисляется его отклонение от средней, т.е. получается множество Т.

3. Каждый элемент множества Т возводят в квадрат.

4. Находится сумма этих квадратов.

5. Эта сумма, как и в случае вычисления среднего, делится на общее количество членов ряда – n. В ряде случаев, особенно когда величина выборки мала, деление осуществляется не на величину n, а на величину n – 1.

Величина, получающаяся после пятого шага, и есть искомая дисперсия.

Преимущество дисперсии перед размахом в том, что дисперсию можно представить как сумму ряда чисел (согласно ее определению), т.е. разложить на составные компоненты, позволяя тем самым более подробно охарактеризовать исходную выборку. Важная характеристика дисперсии заключается также и в том, что с её помощью можно сравнивать выборки, различные по объему.

Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют стандартным отклонением.

Из суммы квадратов, деленных на число членов ряда извлекается квадратный корень.

Другими словами, стандартное отклонение выборки Sx представляет собой корень квадратный, извлеченный из дисперсии выборки. Стандартное отклонение для генеральной совокупности обозначают также символом а. Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают.

В нашем примере

Дата добавления: 2014-12-27