Пример получения полиноминальной модели с проверкой адекватности модели и значимости коэффициентов

Требуется получить полиноминальную модель для индуктивности L многослойной катушки с числом витков равным 100, которая зависит в основном от трех параметров, определяемых конструкцией: диаметром каркаса катушки D, толщинойнамотки b и высотой намотки l. Требуется также провестистатистический анализ полинома и качества эксперимента с проверкой значимости членов полинома и адекватности полинома результатам опыта [20].

Для решения задачи вначале с помощью формулы (3.8) необходимо найти коэффициенты β₀,β _D,β _b и β _l и получить полином:

L = β₀ +β _DD + β _bb + β _ll. (3.8а)

Требуется выбрать номинальные или начальные значения D ₀, b ₀ и l ₀ и отклонения Δ D, Δ b иΔ l, которые будут использованы при эксперименте для нахождения влияния каждого из параметров. Обычно при эксперименте берутся такие отклонения, которые определяются максимально допустимыми значениями. Пусть:

D ₀ = 0.5 см; b ₀ = 0.5 см; l ₀= 1 см;

Δ D = ±0.1 см,Δ b = ±0.1 см; Δ l = ±0.1 см. (3.19)

Для эксперимента можно изготовить восемь катушек, у которых в разных сочетаниях в соответствие с таблицей 3.1 диаметр D составляет 0.4 см (что соответствует -1) или 0.6 см (что соответствует +1); высота намотки l равна 0.4 или 0.6 см; толщинанамотки b равна 0.9 или 1.1 см.

Затем производится измерение индуктивности, что позволяет заполнить столбец у_т. Этих замеров достаточно для вычисления восьми коэффициентов полинома. Предполагая слабое влияние взаимодействий, ограничимся вычислением коэффициентов линейного приближения. Опуская результаты замеров и вычисления по формулам (3.16), приведем в окончательном виде полином, соответствующий (3.12), с нормированными переменными для W = 100:

L = 68 + 7 b ^*+ 12 D ^* - 5 l ^*, (3.12а)

где b ^*, D ^* и l ^* - нормированные переменные, которые могут принимать значения +1 или -1. Избыточность будет использована для статистического анализа полинома и качества эксперимента.

Воспользовавшись (3.15) и учтя (3.19), перейдём от полинома с нормированными переменными (3.12а) к полиному в натуральном масштабе:

;

; ; ; ;

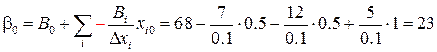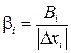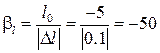L = 23 + 70 b + 120 D - 50 l [мкГн]. (3.8б)

Пользуясь (3.8б), можно производить расчет катушек с разным числом витков и разными размерами, но вблизи от указанных выше поминальных значений с возможными отклонениями от них примерно на ±(24…30)%. Получающиеся при этом результаты будут гораздо более точными, чем при использовании универсальной формулы.

Для анализа точности и стабильности таких катушек удобнее применять уравнение отклонений:

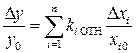, (3.20)

гдеΔ у – отклонение значения выходного параметра от номинальной величины у ₀; Δ x_i – отклонение значения i -ого исходного параметра от номинальной величины x_{i 0}; k_{i ОТН} – коэффициенты в уравнении отклонений, вычисляемые по формуле:

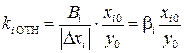; (3.21)

; ;

.

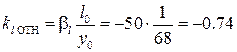Воспользовавшись выражением (3.20), получим:

. (3.20а)

Эксперимент всегда сопровождается ошибками. Эта ошибка может характеризоваться дисперсией D _B(у), которую можно назвать дисперсией воспроизводимости. Наиболее эффективна методика определения дисперсии воспроизводимости, предполагающая g-кратное повторение опыта каждой из строк факторного эксперимента по матрице планирования (таблица 3.1). Обычно g равно 2 или 3. Причем повторные опыты в каждой из строк располагаются в случайной последовательности с другими, то есть план остается рандомизированным. Матрица планирования ПФЭ 2 ^п для п = 3 (ПФЭ 2³) в отличие от таблицы 3.1 будет иметь g + 1 дополнительных столбцов (в таблице 3.2 γ = 2), причём численные значения y_{m РАСЧ} в правом крайнем столбце получают для выходного параметра после расчета по полиному (3.12а).

Таблица 3.2 – Матрица планирования ПФЭ 2 ^п для п = 3 и γ = 2 (ПФЭ 2³)

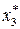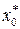
m			-1		…………	ym 1	ym 2	т (ym g) для γ = 2	ym РАСЧ
	–1	–1	–1	+1	…………	у 11	у 12	т (у 1γ) = (у 11 + у 12)/2	y 1 РАСЧ
	+1	–1	–1	+1	…………	у 21	у 22	т (у 2γ) = (у 21 + у 22)/2	y 2 РАСЧ
	–1	+1	–1	+1	…………	у 31	у 32	т (у 3γ) = (у 31 + у 32)/2	y 3 РАСЧ
	+1	+1	–1	+1	…………	у 41	у 42	т (у 4γ) = (у 41 + у 42)/2	y 4 РАСЧ
	–1	–1	+1	+1	…………	у 51	у 52	т (у 5γ) = (у 51 + у 52)/2	y 5 РАСЧ
	+1	–1	+1	+1	…………	у 61	у 62	т (у 6γ) = (у 61 + у 62)/2	y 6 РАСЧ
	–1	+1	+1	+1	…………	у 71	у 72	т (у 7γ) = (у 71 + у 72)/2	y 7 РАСЧ
	+1	+1	+1	+1	…………	у 81	у 82	т (у 8γ) = (у 81 + у 82)/2	y 8 РАСЧ

Среднее значение т (y_{m g})в каждой т -ой строке:

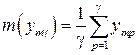, (3.22)

где т – номер строки; р – номер опыта в строке.

Строчная дисперсия:

. (3.23)

Исходя из строчной дисперсии, находим дисперсию воспроизводимости:

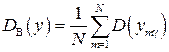. (3.24)

Зная дисперсию воспроизводимости, можно найти дисперсию полиномиальных коэффициентов:

D (B_i) = D _B(y)/ N. (3.25)

Исходя из значений дисперсии воспроизводимости, можно дать статистическую оценку значимости коэффициентов с помощью критерия Стьюдента. Следует отбрасывать те коэффициенты, значение которых соизмеримо с ошибками эксперимента. При этом как бы высказывается гипотеза о незначимости коэффициента, т.е. гипотеза о том, что его действительное значение близко к нулю или равно ему, а его конкретное значение, полученное из результатов опыта, определяется статистическими закономерностями влияния погрешности измерения при малом их количестве. Как известно, по критерию Стьюдента случайная величина t вычисляется по формуле:

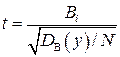, (3.26)

где N – число опытов (строк); D _B(у)– дисперсия разового определения у, т.е. дисперсия воспроизведения, которая точно неизвестна и для которой получена только оценка.

Если т (B_i) = 0, т.е. коэффициент незначим, то величина t распределена по закону Стьюдента и имеет М = (N × γ – N) степеней свободы. Используя таблицу 3.3 распределения Стьюдента и задавшись уровнем значимости a(УЗ), т.е. вероятностью того, что коэффициент будет принят значимым, хотя в действительности он незначим, можно найти соответствующее значение величины t, которое назовем t _ТАБЛ(УЗ) и которое является функцией уровня значимости. Тогда из выражения (3.26) следует, что если:

, (3.27)

то коэффициент следует признать незначимым. Причем с вероятностью, равной уровню значимости, незначимый коэффициент будет признан значимым. Соответственно, если:

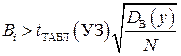, (3.28)

то коэффициент следует признать значимым. Очевидно, что имеется конечная вероятность того, что значимый коэффициент благодаря случайному сочетанию результатов будет признан незначимым (рисунок 3.13). Однако чем больше значимость коэффициента, тем меньше вероятность такого ошибочного решения. После проверки значимости в полиноме оставляют только те коэффициенты, которые признаны значимыми.

В таблице приведены значения квантилей ½ t (M)½_1–a = t _ТАБЛ(УЗ)в зависимости от числа степеней свободы М и уровня значимости (УЗ), то есть вероятности a.

Обработав результаты опытов, приведённые в таблице 3.2, найдем:

- по формуле (3.22) среднее значение т (у_{т g})в каждой т -ой строке;

- по формуле (3.23) строчную дисперсию D (у_{т g});

- по формуле (3.24) находим дисперсию воспроизводимости D _В(у); опуская вычисления, приведём значение этой дисперсии:

D _В(у) = D _В(L)_W=100 = 8.1.

В редких случаях дисперсия воспроизводимости может быть известна априорно, например, если она определяется точностью измерительного прибора, с помощью которого измеряется у. При этом предполагается, что отклонения переменных имеют очень высокую точность. В реальных условиях точность, характеризующая опыт, неизвестна, и должна быть выработана методика вычисления дисперсии воспроизводимости из самого опыта;

Таблица 3.3 – Распределение Стьюдента [16]

Вероятность
a М	0.80	0.40	0.20	0.10	0.05	0.02	0.01	0.001
	0.325	1.376	3.078	6.314	12.706	31.821	63.657	636.619
	0.289	1.061	1.886	2.920	4.303	6.965	9.925	31.598
	0.277	0.978	1.638	2.353	3.182	4.541	5.841	12.941
	0.271	0.941	1.533	2.132	2.776	3.747	4.604	8.610
	0.267	0.920	1.476	2.015	2.571	3.365	4.032	6.859
	0.265	0.906	1.440	1.943	2.447	3.143	3.707	5.959
	0.263	0.896	1.415	1.895	2.365	2.998	3.499	5.405
	0.262	0.889	1.397	1.860	2.306	2.896	3.355	5.041
	0.261	0.883	1.383	1.833	2.262	2.821	3.250	4.781
	0.260	0.879	1.372	1.812	2.228	2.764	3.169	4.587
	0.260	0.876	1.363	1.796	2.201	2.718	3.106	4.437
	0.259	0.873	1.356	1.782	2.179	2.681	3.055	4.318
	0.259	0.870	1.350	1.771	2.160	2.650	3.012	4.221
	0.258	0.863	1.345	1.761	2.145	2.624	2.977	4.140
	0.258	0.866	1.341	1.753	2.131	2.602	2.947	4.073
	0.258	0.865	1.337	1.746	2.120	2.583	2.921	4.015

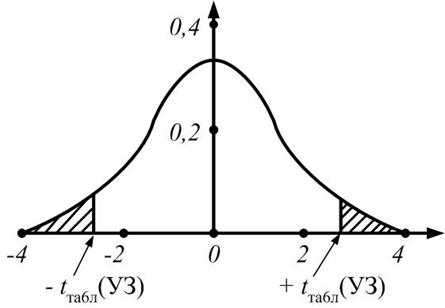
по значениям М и уровню значимости a определяют t _ТАБЛ(УЗ);

площадь заштрихованной области пропорциональна вероятности того,

что отброшенный член полинома является значимым

Рисунок 3.13 – Вид распределения Стьюдента

при числе степеней свободы М = 3

- вычисляем среднее квадратическое отклонение:

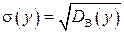; (3.29)

,

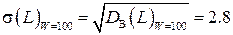что составляет около 3% от номинального значения индуктивности. Как видно, «шум» эксперимента относительно небольшой и опыт воспроизводим с достаточной для практики точностью;

- по формуле (3.25) находим дисперсию полиномиальных коэффициентов:

;

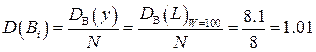- вычисляем среднее квадратическое отклонение коэффициентов:

σ(B_i) = [ D (B_i)]^0.5; (3.30)

оно составляет примерно 1.005. Значения коэффициентов уравнения (3.8б) существенно больше. Следовательно, можно полагать, что все оставшиеся коэффициенты полинома значимы;

- дополнительно производим проверку значимости с использованием критерия Стьюдента. Для уровня значимости, равного a = 0.05 и степеней свободы:

М = (N ×γ – N) = 8×2 – 8 = 8;

из таблицы 3.3 находим t _ТАБЛ(УЗ) = 2.306.

Тогда

.

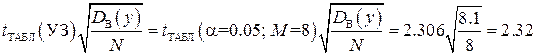Полученное число 2.32 меньше коэффициентов B_i полинома (3.12а):

B ₀ = 68; B ₁ = 7; B ₂ = 12; B ₃ = 5.

Это, согласно (3.28), является подтверждением того, что все коэффициенты полинома значимы;

- производим проверку адекватности. Для проверки адекватности должна быть сохранена избыточность. Сущность ее состоит в сравнении результатов эксперимента для разных сочетаний переменных т (у_{т g}), взятых из таблицы 3.2 с теми результатами, которые при том же сочетании переменных будут получены для параметра после расчета по полиному (3.12а) и занесены в правый крайний столбец этой таблицы. Приведём результаты расчета выходного параметра y_{m РАСЧ} по этому полиному с нормированными переменными:

y_{m РАСЧ} = L_{т РАСЧ} = 68 + 7 b^* + 12 D ^* - 5 l ^*;

y _{1 РАСЧ} = L _1РАСЧ= 68 + 7×(-1)+ 12×(-1)- 5×(-1) = 54;

y _{2 РАСЧ} = L _2РАСЧ = 68 + 7×(+1)+ 12×(-1)- 5×(-1) = 68;

y _{3 РАСЧ} = L _3РАСЧ= 68 + 7×(-1)+ 12×(+1)- 5×(-1) = 78;

y _{4 РАСЧ} = L _4РАСЧ= 68 + 7×(+1)+ 12×(+1)- 5×(-1) = 92;

y _{5 РАСЧ} = L _5РАСЧ= 68 + 7×(-1)+ 12×(-1)- 5×(+1) = 44;

y _{6 РАСЧ} = L _6РАСЧ= 68 + 7×(+1)+ 12×(-1)- 5×(+1) = 58;

y _{7 РАСЧ} = L _7РАСЧ= 68 + 7×(-1)+ 12×(+1)- 5×(+1) = 68;

y _{8 РАСЧ} = L _8РАСЧ= 68 + 7×(+1)+ 12×(+1)- 5×(+1) = 82.

Затем вычисляем дисперсию адекватности:

, (3.31)

где т (у_{т g}) – среднее значение результата эксперимента, взятое из т -ой строки таблицы 3.2, y_{m РАСЧ} – результаты расчета по полиному для того же сочетания переменных; d – количество членов, оставленных в полиноме.

Для D _АД(y)принимается (N – d)степеней свободы, а для D _B(у) берется N ×(γ – 1) степеней свободы.

Для проверки адекватности, то есть проверки гипотез о равенстве дисперсий адекватности D _АД(y) и воспроизводимости D _B(у), вычисляют случайную величину F _АДраспределения Фишера:

. (3.32)

Адекватность полинома результатам опыта может быть установлена из таблицы 3.4 распределения Фишера при сравнении величины F _АДс F _ТАБЛ. В таблице приведены значения квантилей F _ТАБЛ для вероятности a = 0.05 (обычный шрифт) идля a = 0.01 (жирный шрифт) в зависимости от числа степеней свободы М и М ¢: М – число степеней свободы для большей дисперсии, а М ¢ – число степеней свободы для меньшей дисперсии.

По принятому уровню значимости a, т.е. вероятности того, что ошибочно будет отвергнута гипотеза о равенстве дисперсий, по известной функции распределения для F, из таблицы 3.4 находят значение F _ТАБЛ, с которым надлежит сравнивать результаты расчета по формуле (3.32). Если F _АД< F _ТАБЛ, то принимается решение об адекватности полинома результатам опыта (рисунок 3.14).

Для рассматриваемого примера:

- количество членов, оставленных в полиноме d = 4;

- количество степеней свободы для дисперсии адекватности:

(N – d) = 8 – 4 = 4, т.е. М ′ = 4;

- количество степеней свободы для дисперсии воспроизводимости:

N ×(γ – 1) = 8×(2 – 1) = 8, т.е. М = 8;

- расчёт дисперсии адекватности по формуле(3.31) даёт D _АД(y) = 9.1;

- расчёт критерия Фишера F _АДпо формуле(3.32) даёт:

;

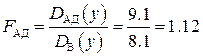из таблицы 3.4 при уровне значимости a = 0.05 с учетом того, что М = 8, a М ′ = 4, получаем F _ТАБЛ = 6.04.

Таблица 3.4 – Распределение Фишера [16]

М М ′											∞
	18.51	19.00	19.16	19.25	19.30	19.33	19.36	19.37	19.39	19.43	19.50
98.49	99.00	99.17	99.25	99.30	9.33	99.34	99.36	99.40	99.44	99.50
	10.13	9.55	9.28	9.12	9.01	8.94	8.88	8.84	8.78	8.69	8.53
34.12	30.82	29.46	28.71	28.24	27.91	27.67	27.49	27.23	26.83	26.12
	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	5.96	5.84	5.63
21.20	18.00	16.69	15.94	15.52	15.21	14.93	14.80	14.54	14.15	13.46
	6.61	5.79	5.41	5.19	5.505	4.95	4.88	4.82	4.74	4.60	4.36
16.26	13.27	12.06	11.39	10.97	10.67	10.45	10.27	10.05	9.63	9.02
	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.06	3.92	3.67
13.74	10.92	9.78	9.15	8.75	8.47	8.26	8.10	7.87	7.52	6.88
	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.63	3.49	3.23
12.25	9.55	8.45	7.85	7.46	7.19	7.00	6.84	6.62	6.27	5.65
	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.34	3.20	2.93
11.26	8.65	7.59	7.01	6.63	6.37	6.19	6.03	5.82	5.43	4.86
	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.13	2.98	2.71
10.56	8.02	6.99	6.42	6.06	5.80	5.62	5.47	5.26	4.92	4.31
	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	2.97	2.82	2.54
10.04	7.56	6.55	5.99	5.04	5.39	5.21	5.06	4.85	4.52	3.91
	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.86	2.70	2.40
9.65	7.20	6.22	5.67	5.32	5.07	4.88	4.74	4.54	4.21	3.60
	4.75	3.88	3.49	3.26	3.11	3.00	2.92	2.85	2.76	2.60	2.30
9.33	6.93	5.95	5.41	5.06	4.82	4.65	4.59	4.30	3.93	3.38

площадь области a равна вероятности ошибочного решения

о неадекватности, а площадь области (1 – a) равна

вероятности ошибочного решения об адекватности

Рисунок 3.14 – Вид распределения Фишера, используемого

Дата добавления: 2014-12-27