Стабилизатора на 18 В на экране монитора

На рисунке 3.9 по результатам граничных испытаний произведено построение области безотказной работы стабилизатора на 18 В при изменении величины сопротивления R 1. В качестве параметра граничных испытаний Х _ГР взято напряжение бортовой сети U _ПИТ, которое по техническим условиям может изменяться в пределах 24…30 В. Температура окружающей среды 27⁰С. На рисунке3.10 по результатам таких же испытаний произведено построение области безотказной работы этого же стабилизатора при изменении величины сопротивления R 6 и при напряжении бортовой сети U _ПИТ = 27 В. В качестве параметра граничных испытаний Х _ГР для этого случая взята температура окружающей среды, меняющаяся от –60⁰С до +60⁰С.

Результаты испытаний показали, что выбранное номинальное значение сопротивления резистора R 1 находится не в центре рабочей области. Поэтому для увеличения параметрической надёжности можно рекомендовать выбрать номинал данного элемента 30 кОм ± 20%, находящийся в рабочей области граничных испытаний при изменении параметров резистора R 1 в пределах ±20% и при температурах от –60°С до +60°С. Коэффициент влияния А_{R 1} изменения сопротивления резистора R 1 на изменение выходного напряжения U _ВЫХ находится по формуле:

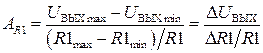. (3.5)

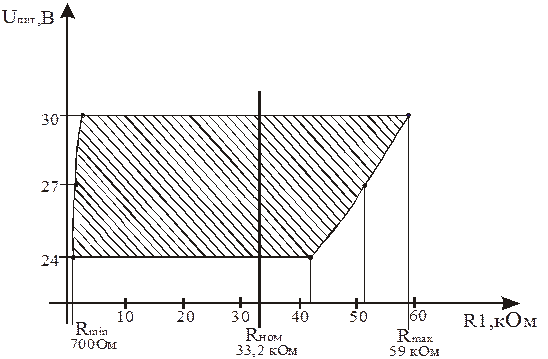
Параметр граничных испытаний – напряжение питания V ₁.

Температура окружающей среды +27⁰С.

Рисунок 3.9 – График, отображающий результаты граничных испытаний стабилизатора напряжения при изменении параметров резистора R 1

(область безотказной работы заштрихована)

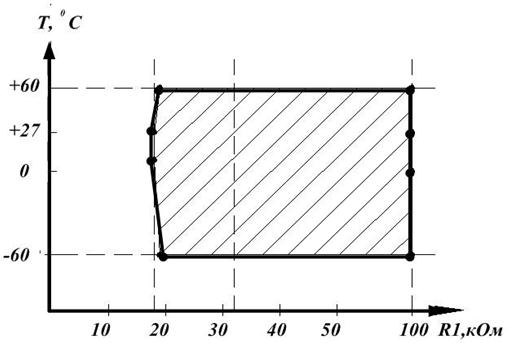
Параметр граничных испытаний – температура окружающей среды,

изменяемая от –60⁰С до +60⁰С

Рисунок 3.10 – График, отображающий результаты граничных

испытаний стабилизатора напряжения при номинальном напряжении питающей сети 27В (область безотказной работы заштрихована)

Таким образом, проведение граничных испытаний дополнительно позволяет определить коэффициенты влияния А_Хi элементов Х_i изделия на его выходной параметр N и составить уравнение погрешностей:

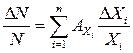, (3.6)

где Δ Х_i – отклонение от номинального значения величины параметра элемента Х_i; n – количество элементов в изделии; Δ N – отклонение от номинального значения величины выходного параметра N.

Переход от погрешностей Δ N / N и Δ Х_i / Х_i к допускам на параметры δ _N и δ _Хi даётся уравнением:

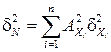. (3.7)

Трудоемкость и затраты времени при проведении граничных испытаний с использованием компьютерной системы схемотехнического моделирования MicroCAP 8 значительно меньше, чем при обычных испытаниях. Намного легче производить изменение параметров элементов. Выдача напряжений и токов для всех элементов, а также построение графиков их частотных и временных зависимостей производится на экране монитора практически мгновенно. Кроме того, при использовании компьютерного моделирования модели являются виртуальными. Поэтому исключаются затраты на изготовление образца для испытаний, а также не требуется производить замену элементов при их отказе.

Справедливости ради, следует отметить и трудности использования компьютерного моделирования, связанные с ограниченностью количества математических моделей элементов в библиотеке MicroCAP 8, а также с ограничением максимального количества элементов в исследуемых моделях. Однако в перспективе во многих случаях испытания на компьютерных моделях вытеснят обычные испытания.

Дата добавления: 2014-12-27