Циклы пересчёта

Переход от одного опорного плана к другому в транспортной задаче сводится к тому, что, как и в симплекс-методе, надо ввести в базис новый вектор вместо выведенного базисного вектора. Это способствует тому, что одну из свободных клеток мы сделаем занятой, т.е. базисной, а одну из базисных – свободной.

Пусть первоначальный опорный план задан таблицей

Таблица 5.5

Пункты отправления	Пункты назначения	Предложение
В1	В2	В3	В4
А1	^5 20	^4 10	^2	^5
А2	^6	^1 70	^1	^3
А3	^2	^3 10	^1 40	^8
А4	^6	^3	^2 30	^1 70
Спрос

Выберем одну из свободных клеток, например (4,1), и поместим в нее некоторую положительную величину перевозки q. Поскольку число занятых клеток должно быть равно m + n - 1, то какую-то из занятых клеток необходимо освободить. Чтобы получить новый опорный план, необходимо пересчитать значения базисных переменных.

Для того, чтобы сумма перевозок в первом столбце не изменилась, нужно перевозку Х₁₁ = 20 уменьшить на величину q. Для того, чтобы при этом не изменилась сумма перевозок в первой строке, надо перевозку Х₁₂ = 10 увеличить на q и т.д.

Пересчет продолжается, пока мы не вернемся к тому значению q, с которого начали, т.е. не замкнем цикл пересчета.

Таблица 5.6

Пункты отправления	Пункты назначения	Предложение
В1	В2	В3	В4
А1	^5 20 - q	^4 10 + q	^2	^5
А2	^6	^1 70	^1	^3
А3	^2	^3 10 - q	^1 40 + q	^8
А4	^6 q	^3	^2 30 - q	^1 70
Спрос					-

Данная операция называется сдвигом по циклу пересчета на величину q. Значение q выбирается равным наименьшему из тех перевозок, из которых q вычитается. В нашем примере выбирается q = 10; если взять q > 10, то перевозка Х₃₂ станет меньше нуля, а если взять q < 10, то получим больше, чем m+n-1 отличную от нуля перевозку, т.е. новый план тогда не будет опорным.

Переход от одного опорного плана к другому связан с некоторым обходом по замкнутой ломаной линии, начало которой находится в свободной клетке, а все остальные вершины в некоторых базисных (занятых) клетках. Если ломаная линия, образующая цикл, пересекается сама с собой, то точки пересечения не являются вершинами. Циклы могут быть различной формы (рис. 72).

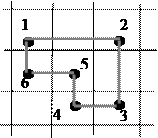
Рис. 72. Возможные формы циклов пересчёта

Вершин в цикле всегда четное число. Цикл, одна из вершин которого лежит в свободной клетке, а все остальные – в базисных, называется циклом пересчета данной свободной клетки.

Каждый опорный план обладает следующими свойствами:

1) не существует циклов, все вершины которых лежат в базисных клетках;

2) для каждой свободной клетки существует единственный цикл пересчета.

В общем случае, для того чтобы определить q, припишем каждой вершине цикла определенный знак таким образом, чтобы две соседние вершины имели противоположные знаки, а вершина, лежащая в свободной клетке, была всегда положительна, т.е. приписываем ей знак (+). Поскольку число вершин в цикле четное, то число положительных вершин будет равно числу отрицательных. При сдвиге по циклу пересчета на величину q перевозки в положительных вершинах цикла увеличиваются на величину q, а в отрицательных – уменьшаются на q. Следовательно, величину q надо выбирать равной наименьшей из перевозок в отрицательных вершинах:

Таблица 5.7

Пункты отправления	Пункты назначения	Предложение
В1	В2	В3	В4
А1	^5 20 -	^4 10 +	^2	^5
А2	^6	^1 70	^1	^3
А3	^2	^3 10 -	^1 + 40	^8
А4	^6 q +	^3	^2 - 30	^1 70
Спрос					-

Определим, как изменится функция цели (стоимость перевозок) при переходе к новому опорному плану:

+q × 6 - q × 5 + q × 4 - q × 3 + q × 1 - q × 2 =

= q× (6 – 5 + 4 – 3 + 1 - 2) = +q × 1.

Следовательно, функция цели увеличится на величину q, а значит, клетка (4,1) для новой перевозки выбрана неудачно:

f(x) = 410 + q = 410 + 10 = 420 ден.ед.

Для того чтобы перейти к лучшему опорному плану, с меньшей функцией цели, можно воспользоваться распределительным методом решения транспортных задач.

Открытая транспортная задача

Если не соблюдается баланс предложения и спроса, то есть

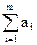¹ ,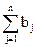

то такая задача называется открытой. Для решения такой задачи, если общее предложение превышает общий спрос, то есть

> ,

необходимо ввести в модель фиктивный пункт потребления (В_n+1) в n + 1-м столбце матрицы транспортной задачи. При этом стоимости перевозки для фиктивного пункта потребления равны нулю:

C_i,n+1 = 0; i = .

Потребность в грузе фиктивного пункта назначения равна разности предложения и спроса.

Таблица 5.8

Пункты отправления	Пункты назначения	Запасы (предложение)
В1	…	Вj	…	Вn	(Вn+1)
А1	С11		C1j		C1n		а1
…		…		…
Аi	Сi1		Сij		Сin		аi
…		…		…
Аm	Сm1		Сmj		Сmn		аm
Потребности (спрос)	b1	…	bj	…	bn	(bn+1 = Sаi - Sbj)

Если величина суммарного спроса превышает суммарное предложение, то есть

< ,

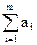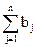необходимо ввести в модель фиктивный пункт отправления грузов (А_m+1) в m + 1-ю строку матрицы транспортной задачи. При этом стоимости перевозки от фиктивного пункта отправления равны нулю:

C_m+1,j = 0; j = .

Предложение фиктивного пункта отправления равно разности суммы потребностей и запасов грузов.

Таблица 5.9

Пункты отправления	Пункты назначения	Запасы (предложение)
В1	…	Вj	…	Вn
А1	С11		C1j		C1n	а1
…		…		…
Аi	Сi1		Сij		Сin	аi
…		…		…
Аm	Сm1		Сmj		Сmn	аm
(Аm+1)						(am+1 = Sbj - Sаi)
Потребности (спрос)	b1	…	bj	…	bn	^__

Дата добавления: 2014-12-27