
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матричные игры
|
|
|
|
Основные понятия теории игр. При решении задач в области экономики и управления производством в условиях неполноты и неточности информации возможны ситуации, когда необходимо принятие решений в условиях риска и неопределенности.
Предметом изучения теории игр являются ситуации, когда отсутствует полнота информации, а аппарат теории игр предназначен для выбора оптимальных решений в условиях неопределенности. Методы теории игр разработаны применительно к специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Целью теории игр является выработка рекомендаций по рациональному образу действия участников многократно повторяющегося конфликта. Под конфликтными ситуациями понимается положение, когда сталкиваются интересы двух и более сторон, причем выигрыш зависит от того, как поведут себя другие стороны. Математический анализ конфликта возможен при построении математической модели конфликта. Такая модель называется игрой. От реального конфликта игра отличается тем, что ведется по определенным правилам, которые участникам конфликта известны и строго выполняются. Игра называется парной, если в ней участвуют две стороны. Если в парной игре выигрыш одного из игроков равен проигрышу другого, то такая парная игра называется игрой с нулевой суммой. Конечной игрой называется игра с конечным числом стратегий. Стратегией называется совокупность правил, определяющих выбор варианта действия при каждом ходе в зависимости от сложившейся ситуации. Ходы бывают личные и случайные. При случайном ходе – выбор стратегии случайный. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает ему максимальный средний выигрыш или минимальный средний проигрыш.
|
|
|
Пусть игрок А имеет m чистых стратегий А1, А2, … Аi,…Аm, а игрок В имеет n чистых стратегий B1, B2, … Bj,…Bn. Такая игра называется игрой m ´ n. Если игрок А пользуется стратегией Аi, а игрок В пользуется стратегией Вj, то обозначим через аij выигрыш игрока А, если аij > 0, или проигрыш игрока А, если аij < 0. Очевидно, что – это одновременно проигрыш игрока В, если аij > 0, и выигрыш игрока В, если аij < 0.
Тогда мы можем привести игру к матричной форме, т.е. составить матрицу, которая называется платежной матрицей, или матрицей игры:
| В1 | В2 | … | Вj | … | Вn | ||
| А1 | а11 | а12 | … | а 1j | … | а 1n | |
| … | … | … | … | … | … | … | (7.1) |
| Аi | аi1 | а i2… | … | а ij | … | а in | |
| … | … | … | … | … | … | … | |
| Аm | аm1 | а m2 | … | а mj | … | а mn |
Каждая строка этой матрицы соответствует некоторой стратегии игрока А, а каждый столбец – некоторой стратегии игрока В.
Пример игры. Два игрока выкидывают на пальцах числа, причем четное число пальцев – это выигрыш игрока А, нечетное – проигрыш игрока А. Для простоты введем ограничение – игроки выкидывают от 1 до 3 пальцев.
Составим платежную таблицу:

| В1 | В2 | В3 | 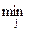
|
| А1 | -3 |  -3 -3
| ||
| А2 | -3 | -5 | -5 | |
 А3 А3
| -5 | -5 | ||
   
| ||||
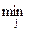
|
Проанализируем матрицу игры: для каждой чистой стратегии игрока А определим минимальный выигрыш, т.е. определим
ai = 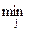 аij.
аij.
В нашем примере a1 = -3; a2 = -5; a3 = -5. Далее, среди полученных значений li-х определим максимальное
a = 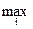 ai =
ai = 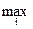
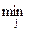 аij.
аij.
В нашем примере a = -3, т.е. игрок А проигрывает 3 очка. Это число a называется нижней ценой игры, а соответствующая ему стратегия называется максиминной. В нашем примере стратегия А1 максиминная, т.е. из всех наихудших ситуаций выбирают наилучшую. Эта величина (a) – гарантированный «выигрыш» игрока А, какую бы стратегию ни выбрал игрок В. Меньше нижней цены игры игрок А никогда не «выиграет», если будет придерживаться правил игры.
|
|
|
Игрок В старается максимально уменьшить свой проигрыш. Для этого определяется верхняя цена игры
b = 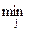 bj =
bj = 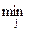
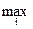 аij.
аij.
Соответствующая стратегия называется минимаксной. В нашем примере будет две минимаксных стратегии В1 и В2. При этом игрок В проигрывает 4 очка.
Теорема 1. В любой матричной игре справедливо неравенство a £ b, т.е. нижняя цена игры никогда не превосходит верхнюю.
Игра с седловой точкой
Если в матричной игре нижняя и верхняя цены игры совпадают, то такая игра имеет «седловую точку» в чистых стратегиях, а число u = a = b называют ценой игры. В этом случае решением игры, т.е. оптимальным поведением для обоих игроков являются их максиминная для игрока А и минимаксная для игрока В стратегии игры. Любое отклонение игроков от своих оптимальных стратегий не может оказаться им выгодным. Элемент платежной матрицы, отвечающий оптимальным стратегиям, называется седловой точкой.
Пример. Пусть игра задана следующей платежной матрицей:

| В1 | В2 | В3 | В4 | ai | ||
| |||||||
| А2 | |||||||
   А3 А3
| |||||||
 А4 А4
| |||||||
   bj bj
| |||||||
| цена игры u = a = b = 4 | |||||||
| min max - лучшая стратегия для игрока В – (В2) |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 572; Нарушение авторских прав?; Мы поможем в написании вашей работы!
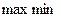 -
лучшая
стратегия
для игрока
А – (А3)
-
лучшая
стратегия
для игрока
А – (А3)