Исследованиях

Применение матричных игр в маркетинговых

Игры 2 х n и m х 2

Допустим, платежная матрица задана и имеет вид 2 х n:

	В1	В2	…	Вn	Игрок А имеет две стратегии, а игрок В – неограниченное число стратегий.
А1	a11	a12	…	a1n
А2	a21	a22	…	a2n

Допустим, платежная матрица имеет вид m х 2:

Минимум М находится на пересечении стратегий А₁ и А_m, остальные отбрасываются, далее игра решается как задача 2 х 2.

Пример. Пусть игра задана в виде платежной матрицы

	В1	В2	В3	Игра (2 х 3) не имеет седловой точки a = 4, b = 5, a ¹ b, имеем игру в смешанных стратегиях.
А1
А2

Решим задачу графически и аналитически. Для игрока А: получаем игру 2 х 2, используя стратегии В₂ и В₃ игрока В:

Для игрока В:

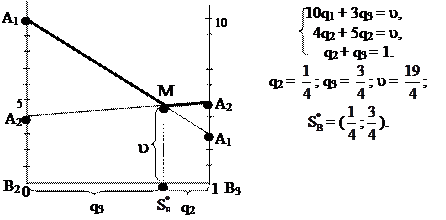
Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющей­ся конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в табл. 7.1.

Определить оптимальный план продажи товаров.

Решение. Обозначим: вероятность применения торговой фирмой стратегии П₁ — х₁ стратегии П₂ — х₂, П₃ — х₃; ве­роятность использования стратегии К₁ — у₁, стратегии К₂ — у₃, К₃ — у_3.

Таблица 7.1

План	Величина дохода, ден. ед.
продажи	К1	К2	К3
П1
П2
П3

Для первого игрока (торговой фирмы) математическая мо­дель задачи имеет вид

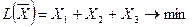
при ограничениях:

8Х₁ + 2Х₂ + Х₃ ≥ 1,

4Х₁ + 8Х₂ + 2Х₃ ≥ 1,

2Х₁ + 4Х₂ + 8Х₃ ≥ 1,

X_i ≥ 0, i = 1,3,

где х_i = Х _iV

Для второго игрока (конъюнктуры рынка и спроса покупа­телей) математическая модель задачи имеет вид

при ограничениях:

8Y₁ + 4Y₂ + 2Y₃ ≤ 1,

2Y₁ + 8Y₂ + 4Y₃ ≤ 1,

Y₁ + 2Y₂ + 8Y₃ ≤ 1,

Y_j ≥ 0, j = 1,3.

Найдем оптимальное решение задачи для второго игрока симплексным методом. При этом последняя таблица имеет вид табл. 7.2.

Из таблицы следует, что 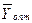= (1/14,11/196,5/49), = 45/196.

Цена игры v = 1/S(У) = 196/45.

Так как у_i = У _iv, то y₁ = 14/45, y₂ = 11/45, уз = 20/45.

Таблица 7.2

bj	БП							Ci
	Y1	Y2	Y3	Y4	Y5	Y6
	Y1				1/7	-1/14		1/14
	Y2				-3/98	31/196	-1/14	11/196
	Y3				-1/98	-3/98	1/7	5/49
Di				5/49	11/196	1/14	45/196

Оптимальная стратегия второго игрока:

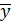_опт = (14/45,11/45,20/45).

Стратегии первого игрока найдем из последней симплекс­ной таблицы, используя метод соответствия переменных ис­ходной и двойственной задач. Получим

_опт =(20/45,11/45,14/45).

Таким образом, торговая фирма на ярмарке должна при­держиваться стратегии _опт =(20/45,11/45,14/45), при этом она получит доход не менее

V=196/45 ден. ед.

УПРАЖНЕНИЯ

Найти оптимальные стратегии и цену игры.

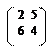7.1. А=. 7.2. А=. 7.3. А=

7.4. А=. 7.5. А=.

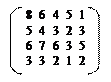7.6. А=. 7.7. А=.

Построить игру, заданную задачей линейного программирования.

7.8. L(х) = х ₁+ 2x ₂ – x ₃ max при ограничениях:

x ₁+ х ₂ – х ₃ ≤ 1,

2 x ₁ – 3 x ₂ + x ₃ ≤ 2,

х _j ≥ 0, j = 1,3.

Решить задачу с использованием матричных игр.

7.9. Розничное торговое предприятие разработало несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели прибыли представлены в табл. 7.3.

Определить: а) оптимальный план продажи товаров и цену игры;

б) какой стратегии следует придерживаться торговому предприятию, если наиболее вероятной является ситуация: С ₁ — 30%, С ₂ — 30%, С₃ — 40%?

Таблица 7.3

План продажи	Величина прибыли в зависимости от спроса, млн р.
С 1	С 2	С 3
П 1
П 2
П 3

7.10. Предприятие планирует выпуск трех партий новых видов товаров широкого потребления в условиях неясной рыночной конъюнктуры. Известны отдельные возможные состояния P ₁, P ₂, Р ₃, Р ₄, а также возможные объемы выпуска изделий по каждому варианту и их условные вероятности, которые представлены в табл. 7.4.

Таблица 7.4

Изделия	Объем выпуска изделий при различных состояниях рыночной конъюнктуры
Р 1	Р2	Р 3	Р 4
И1	0,4 2,2	0,1 3,8	0,2 2,8	0,3 3,2
И2	0,3 2,6	0,2 2,4	0,1 3,1	0,4 3,3
И3	0,2 3,0	0,3 2,0	0,2 1,8	0,3 2,5

Определить предпочтительный план выпуска товаров широкого потребления.

7.11. Фирма производит пользующиеся спросом детские платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение августа-сентября на единицу продукции составили: платья — 7 ден. ед., костюмы — 28 ден. ед. Цена реализации составляет 15 и 50 ден. ед. соответственно.

По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды 1950 платьев и 610 костюмов, а при прохладной погоде — 630 платьев и 1050 костюмов.

В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход от реализации продукции. Задачу решить графическим методом и с использованием критериев "природы", приняв степень оптимизма α = 0,5.

Дата добавления: 2014-12-27