Игра в смешанных стратегиях

Если платежная матрица не имеет седловой точки, то если игрок будет пользоваться смешанными стратегиями, т.е. при каждом ходе менять стратегию случайным образом, то игрок А выигрывает больше, чем a, а игрок В проигрывает больше, чем b.

Рассмотрим платежную матрицу (7.1). Пусть игрок А использует чистые стратегии А₁, А₂, … А_i,…А_m с вероятностями p₁, p₂, … p_i,…p_m, причем 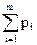=1, а игрок В использует свои чистые стратегии В₁, В₂, … В_j,…B_n с вероятностями q₁, q₂, … q_j,… q_n, причем 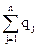= 1.

Тогда набор S_A = (p₁, p₂, … p_i,…p_m) называется смешанной стратегией игрока А, а набор S_B = (q₁, q₂, … q_j,… q_n) - смешанной стратегией игрока В.

Поскольку игроки выбирают свои стратегии случайным образом, то вероятность выбрать комбинацию А_iВ_j по теории вероятности равна (P_i × q_j). При использовании смешанных стратегий игра становится случайной, тогда говорят о среднем значении выигрыша, который определяется платежной функцией

f(S_A, S_B) = 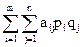. (7.2)

Смешанные стратеги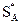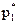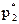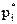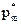и = (, ,… … ) и 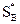= (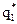, ,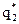… … 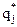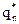) называются оптимальными, т.е. дающими каждой стороне максимальный возможный для нее средний выигрыш (для А) или минимальный средний проигрыш (для В), если они образуют седловую точку для платежной функции (7.2), т.е. если выполняется следующее условие:

f(S_A, 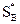) £ f(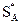, 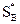) £ f(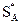, S_B).

Величина u = f(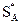, S_B) называется ценой игры.

Теорема 2. В смешанных стратегиях любая матричная игра имеет седловую точку, или каждая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.

Дата добавления: 2014-12-27