Плотностью распределения случайной величины называется функция

(x) = F’(x)

Плотность распределения любой случайной величины не отрицательна (х) ³ 0. Основным свойством функции (x) является равенство ее интеграла единице в пределах возможного интервала изменения значений случайной величины.

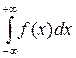= 1 (3.28)

График плотности распределения (x) называется кривой (законом) распределения.

Элементом вероятности для случайной величины Х называется величина (x)dх, приближенно выражающая вероятность попадания случайной точки Х в элементарный отрезок dx, примыкающий к этой точке. График плотности распределения демонстрирует изменение вероятности появления каждого конкретного значения случайной величины, рис. 19.

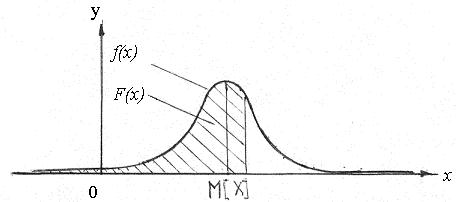
Рис. 19. Вид функции f(x) и F(x)

На этом рисунке заштрихованная область соответствует вероятности того, что случайная величина Х примет значение меньше заданного значения х (определяется по формуле (3.27)); М[ X ] – математическое ожидание величины Х.

Математическим ожиданием непрерывной величины Х называется ее среднее значение, вычисленное по соотношению

М[ X ] = 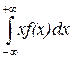(3.29)

Дисперсией непрерывной случайной величины называется величина, характеризующая разброс значений случайной величины относительно ее математического ожидания

D[ X ] = (3.30)

Средним квадратическим отклонением s случайной величины Х называется корень квадратный из дисперсии

s [ X ] = 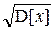(3.31)

Вероятность попадания случайной величины Х на участок, протяженностью от a до b, находится по соотношению:

Р(a £ Х £ b) = 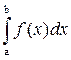= F(b) – F(a) (3.32)

Во многих случаях распределение случайной величины подчиняется нормальному закону распределения.

Непрерывная случайная величина Х называется распределённой по нормальному закону, если плотность её распределения подчинена зависимости

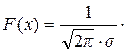exp[ 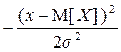] (3.33)

Вероятность попадания случайной величины Х, распределённой по нормальному закону, в интервал (a,b) находится по соотношению (по аналогии с (3.32))

Р (a £ Х £ b) =Ф()-Ф(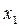) = 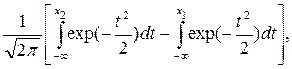(3.34)

где 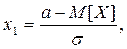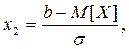Ф ()=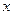

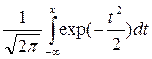
Функция Ф (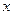)–табулированная функция Лапласа. В приближенных расчетах пользуются аппроксимациями этой функции.

Для оценки вероятности поражения объекта профессором В. В. Яковлевым рекомендовано использовать аппроксимацию, предложенную Ф. А. Евстифеевым, удобную в практических расчетах [22]:

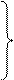
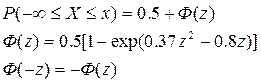, (3.35)

где z 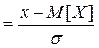- нормированное отклонение случайной величины.

Соотношение (3.35) можно представить в виде:

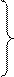
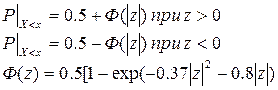(3.36)

Учитывая особенности нормального закона распределения, для которого вероятность реализации случайной величины, значения которой не превосходят M[ X ] 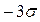, составляет 0,0014, а вероятность реализации случайной величины, значения которой не превосходят M[ X ] , составляет 0,9984, можно сказать, что в случае, если значение случайной величины укладывается в интервал (M[ X ] 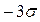, M[ X ] ), то вероятность её реализации практически равна единице.

С учетом данного допущения значения математического ожидания M, среднеквадратического отклонения 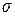и нормированного отклонения Z случайной величины при определении вероятности поражения объекта при пожаре находятся по соотношениям:

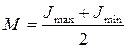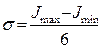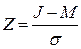; ; , (3.37)

где 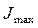- максимальное значение параметра, определяющего нижнюю границу значений безусловного поражения объекта;

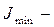минимальное значение параметра, определяющего верхнюю границу значений безопасности объекта;

воздействующее значение параметра (интенсивность теплового облучения), для которого рассчитывается вероятность поражения человека.

Зная (или определив) величины , , 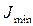, 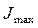по соотношениям (3.37) находят значения 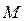, , 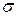z и по соотношениям (3.36) определяют вероятность поражения объекта.

При прогнозировании развития и распространения пожара большое значение имеет определение параметрического и координатного законов поражения.

Параметрическим законом поражения называется зависимость вероятности поражения объекта от заданных значений характеристик поражающего фактора (в рассматриваемом случае-интенсивности теплового облучения).

Алгоритм построения параметрического закона поражения:

- определить значения поражающего фактора, характеризующие безопасность и безусловное поражение объекта;

- задаться количеством рассматриваемых точек и соответствую-щими значениями воздействующего фактора в каждой точке выбранного интервала;

- по формулам (3.37) вычислить для каждого заданного значения воздействующего фактора соответствующие параметры нормального закона распределения;

- по формуле (3.36) найти вероятности поражения объекта, соответствующие каждому значению поражающего фактора;

- построить график изменения вероятности поражения объекта при различных значениях воздействующего фактора.

Ниже рассматривается пример построения параметрического закона поражения при задании значений поражающих факторов, характеризую-щих безопасность и безусловное поражение объекта, в общем виде.

Пример. Построить параметрический закон поражения здания при пожаре, если интенсивность теплового облучения, определяющая нижнюю границу значений безусловного поражения (возгорания) здания, составляет 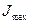,безопасное значение интенсивности теплового облучения

Решение. 1. В пределах диапазона интенсивностей теплового облучения от до

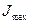зададимся несколькими значениями 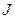с шагом, например, 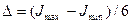. Для каждого значения 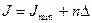,где n =0,1,2…6 по соотношениям (3.37) вычисляем значения параметров нормального закона распределения 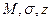и по соотношениям (3,36) - соответствующие вероятности поражения P.

Результаты расчетов сведены в табл. 22.

Таблица 22

Дата добавления: 2014-12-27