Метод гармонической линеаризации

Основные теоретические положения

Многоконтурная нелинейная система (НС) представляется в одноконтурном виде (рис.3.1). Применительно к курсовой работе будем рассматривать однозначные (беспетлевые) нелинейные характеристики, описываемые выражением

. (3-1)

Рис. 3.1.

Линейная часть описывается частотной передаточной функцией

, (3-2)

где - модуль передаточной функции; - аргумент передаточной функции.

Метод гармонической линеаризации основан на двух допущениях:

а) в замкнутой системе по каким-либо причинам существуют периодические колебания;

б) линейная часть обладает свойством фильтра, т.е. ослабляет высокочастотные составляющие периодических колебаний:

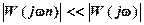, n = 2,3...

При этом колебания на входе НЭ приближенно имеют синусоидальный характер симметричного

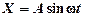(3-3)

или несимметричного вида с постоянной составляющей Хо

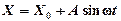(3-4)

В курсовой работе рассматриваются нелинейные характеристики с нечетной симметрией, внешние возмущения отсутствуют (g(t)=0). В этом случае постоянная составляющая Хо=0. Поэтому гармоническая линеаризация выражения (3-1) проводится при симметричных колебаниях (3-4).

Гармонически линеаризованное уравнение (3-1) имеет вид

, (3-5)

где и 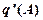– коэффициенты гармонической линеаризации.

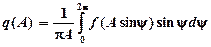(3-6)

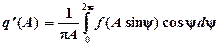, (3-7)

Амплитудно-фазовая характеристика нелинейного звена в результате подстановки имеет вид

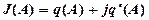. (3-8)

Для однозначных нелинейностей , поэтому

. (3-9)

Методика вычислений коэффициентов гармонической линеаризации изложена в [1], выражения коэффициентов для различных нелинейностей приведены в [2].

Прежде чем перейти к нахождению периодических режимов, остановимся на структурных преобразованиях в НС. Для определения устойчивости периодических режимов в НС структурные схемы приводятся к виду (рис.3.1) с помощью линейных и нелинейных преобразований. Особенность структурных преобразований в НС состоит в том, что независимо от вида преобразований амплитуда сигнала на входе НЭ не должна измениться, поэтому нельзя переносить линейные звенья через НЭ. При линейных преобразованиях передаточные функции замкнутой системы до и после преобразований совпадают (рис.3.2).

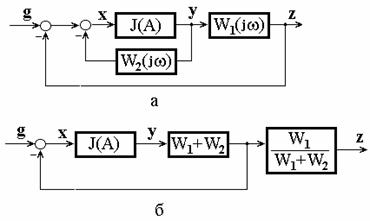
Рис. 3.2. Линейные преобразования структурных схем

Передаточная функция системы до преобразования (рис.3.2,а)

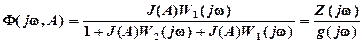, (3-10)

и после преобразований (рис.3.2,б)

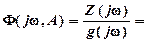
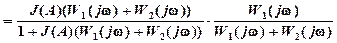(3-11)

совпадают, следовательно, эти преобразования эквивалентны и позволяют исследовать не только устойчивость, но и строить переходные процессы по преобразованной схеме.

Нелинейные преобразования [3] структурных схем не являются эквивалентными и позволяют исследовать только устойчивость собственного движения системы. При правильно преобразованных схемах характеристические уравнения замкнутых систем должны совпадать.

После преобразования структурной схемы системы к одноконтурному виду и гармонической линеаризации нелинейности необходимо частотным методом исследовать возможность возникновения устойчивых периодических режимов (автоколебаний). Характеристическое уравнение замкнутой системы

(3-12)

преобразуется (по методу Л.С. Гольдфарба) к виду

(3-13)

Согласно методу на комплексной плоскости строятся годографы 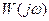и . Если эти годографы пересекаются, то возможен периодический режим, устойчивый при выполнении условия

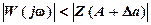, (3-14)

При использовании логарифмических характеристик для определения автоколебательных режимов проверяется выполнение условий баланса амплитуд

(3-15)

и баланса фаз

. (3-16)

Переходя к логарифмическим характеристикам и учитывая, что для однозначных нелинейностей , вместо (3-15) и (3-16) можно записать:

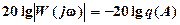, (3-17)

. (3-18)

Обозначим ,

Условие устойчивости автоколебаний имеет вид:

. (3-19)

Звездочкой обозначены те значения амплитуды А и частоты при которых выполняются условия (3-17) и (3-18).

Графоаналитические исследования периодических режимов в отчете можно представить на комплексной плоскости (см.пример 3.1) или в логарифмических координатах в соответствии с [1].

Пример 3.1.: Дано:

W1(S) = 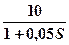; W2(S) = ; W3(S) = .

Нелинейный элемент типа «зона нечувствительности»: a = 20 В; tg a = 1.

Нелинейный элемент расположен в прямой цепи двухконтурной системы (положение 1). В этом случае приведенная ко входу нелинейного элемента структурная схема примет вид, показанный на рис. 3.3.

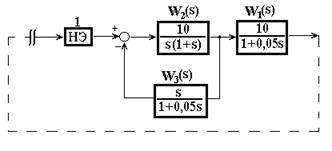
Рис.3.3 Структурная схема, приведенная ко входу нелинейного элемента.

Передаточная функция разомкнутой системы определяется выражением

W(S) = = = ,

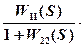
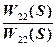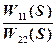
где W11(S) = ;

W22(S) = .

L(w) = ;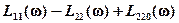

j(w) = ,

где , - соответственно ЛАХ и ЛФХ замкнутого внутреннего контура, определяемые из номограммы замыкания по и .

Данные вычислений сведены в табл. 3.1, ЛАХ и ЛФХ показаны на рис. 3.4, АФХ линейной части и характеристика нелинейный элемента - на рис. 3.5 Из рис. 3.5 видно, что условия гармонического баланса не выполняются, автоколебаний в системе не будет.

Качественно построенные переходные функции при малых и больших амплитудных значениях управляющего воздействия (величины рассогласования) показаны на рис. 3.6.

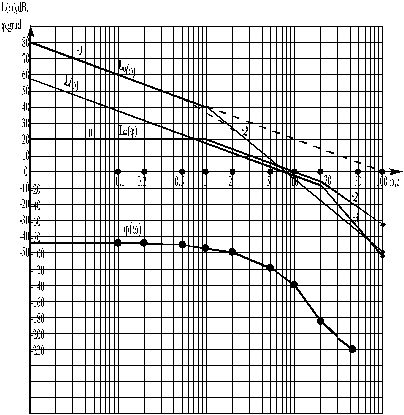
Рис.3.4ЛАХ и ЛФХ линейной части системы

Рис. 3.5. АФХ линейной части и гармоническая характеристика нелинейного элемента

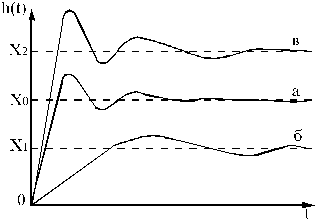
Рис. 3.6. Переходные процессы системы: a - линейной; б - нелинейной при малых амплитудах; в - нелинейной при больших амплитудах

Табл. 3.1

Характеристики	Значения
	0.1	0.2	0.5
1/p	-90	-90	-90	-90	-90	-90	-90	-90	-90	-90
1/1+p	-5	-12	-25	-45	-62	-78	-83	-88	-90	-90
1/1+0,05p				-2	-7	-15	-25	-45	-67	-80
	-95	-102	-115	-137	-159	-183	-198	-223	-247	-260
	-5	-12	-25	-47	-69	-93	-108	-133	-157	-160
								-5	-22	-31
	-0.8	-0.8	-0.8	-0.8	-0.75	-0.75	-0.75	-3.5	-20	-41
				-5	-10	-25	-50	-95	-150	-160
	-90	-90	-90	-95	-100	-115	-140	-185	-240	-260
								-10	-35	-52
	39.2	34.2	24.2	19.2	12.2	4.2	-0.75	-8.5	-33	-52

Пример 3.2. Дано:

W1(S) = 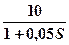; W2(S) = ; W3(S) = .

Нелинейный элемент типа зона нечувствительности: с = 20 В; tg a = 1.

Нелинейный элемент расположен в цепи корректирующей обратной связи (положение 3). В этом случае приведенная ко входу нелинейного элемента структурная схема примет вид, показанный на рис. 3.7.

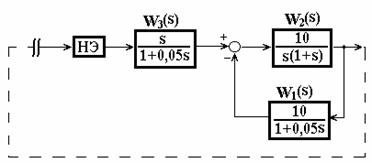
Рис. 3.7. Структурная схема, приведенная ко входу нелинейного элемента

Передаточная функция разомкнутой системы определяется выражением

W(S) = = = .

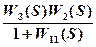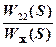ЛАХ и ЛФХ вычисляются по формулам:

L() = ;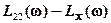

() = .

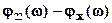ЛАХ звена может быть определена с помощью номограммы замыкания по путем замены знаков пр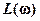и и на противоположные. В нашем случае достаточно изменить знаки 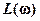, .Тогда

L() = ,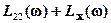

() = .

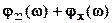Данные вычислений сведены в табл. 3.2. ЛАХ и ЛФХ показаны на рис. 3.8, АФХ линейной части и характеристика нелинейный элемента – на рис. 3.9. Изображенная на рис. 3.9 АФХ соответствует системе, неустойчивой в разомкнутом состоянии и устойчивой в замкнутом, и при анализе устойчивости автоколебаний используется обобщенный критерий Найквиста. В нашем случае имеем:

W(S) = = = .

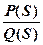Устойчивость в разомкнутом состоянии можно проанализировать путем исследования характеристического уравнения , а в замкнутом - :

.

Рис. 3.8. ЛАХ и ЛФХ линейной части нелинейной системы

Табл. 3.2

	Значения
Характеристики	0.1	0.2	0.5
	-60	-55	-45	-37	-28	-12	-1
	-60	-55	-45	-37	-28	-9.2		1.8
								-5	-22	-33
	-5	-12	-25	-47	-69	-93	-108	-133	-157	-160
	-40	-35	-25	-20	-13	-2.2		-3.2	-22	-33

Условие устойчивости по Гурвицу имеет вид .

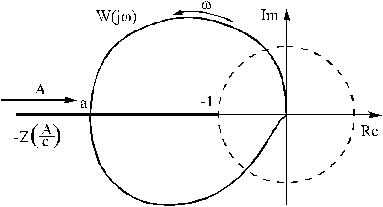
Рис. 3.9. АФХ линейной части системы и гармоническая характеристика нелинейного элемента

Так как , , , , , 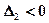система неустойчива в разомкнутом состоянии. Используя теорему разложения, легко показать, что характеристическое уравнение имеет один отрицательный вещественный корень и два комплексно-сопряженных корня с положительной вещественной частью. Анализируя 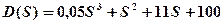, получим 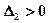, что указывает на устойчивость системы в замкнутом состоянии.

Из рис. 3.8 и 3.9 видим, что условия гармонического баланса выполняются, и на основании критерия устойчивости автоколебаний делаем заключение, что в системе с нелинейным элементом типа зона нечувствительности, расположенным в цепи корректирующей обратной связи, возникают устойчивые автоколебания в точке а с параметрами

, .

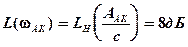По графику зависимости:

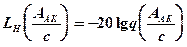определим: , .

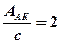Дальнейший расчет и анализ рекомендуется провести самостоятельно.

Дата добавления: 2014-12-27