
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интерполяционная формула Лагранжа. Единственность интерполяционного многочлена
|
|
|
|
Единственность интерполяционного многочлена
Задача интерполирования имеет единственное решение. Для доказательства допустим, что имеются два многочлена Ln(x) и Mn(x), оба не выше n -ой степени, удовлетворяющие условию (1) задачи:
Ln(xi)=f(xi), Mn(xi)=f(xi), i=0,1,…,n.
Разность этих многочленов Pn(x)= Ln(x)- Mn(x) является многочленом степени не выше n и обращается в нуль во всех узлах интерполяции Pn(xi)= Ln(xi)- Mn(xi)= f(xi)- f(xi)=0.
Следовательно, уравнение Pn(x)=0 имеет n+1 корень. Уравнение n -ой степени не может иметь больше, чем n вещественных корней, поэтому многочлен Pn(x) тождественно равен нулю, т.е. Ln(x)- Mn(x) ≡ 0 или Ln(x) ≡ Mn(x).
Независимо от способа построения интерполяционного многочлена, в конечном результате всегда получается один и тот же многочлен, а представляющие его формулы могут быть различными.
Каждому узлу интерполяции 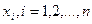 , сопоставим многочлен
, сопоставим многочлен
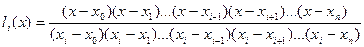 . (1)
. (1)
Многочлен  равен нулю в любом узле интерполяции
равен нулю в любом узле интерполяции  , отличном от узла
, отличном от узла 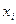 , так как в числителе имеется множитель
, так как в числителе имеется множитель 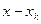 , который обращается в нуль при
, который обращается в нуль при  .
.
В узле 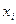 многочлен
многочлен  принимает значение равное единице, так как при
принимает значение равное единице, так как при  числитель и знаменатель совпадают
числитель и знаменатель совпадают  ,
,
Докажем, что интерполяционный многочлен 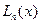 можно представить формулой:
можно представить формулой:
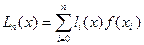 (2).
(2).
Правая часть равенства (2) является многочленом степени не выше n. В узлах интерполяции  её значение равно:
её значение равно:
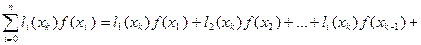
 ,
,
при  все числа
все числа  , а при
, а при 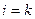
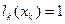 . Многочлен представленный формулой (2), удовлетворяет всем условиям задачи. Формула (2) называется интерполяционной формулой Лагранжа в развернутой форме:
. Многочлен представленный формулой (2), удовлетворяет всем условиям задачи. Формула (2) называется интерполяционной формулой Лагранжа в развернутой форме:
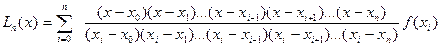 (3)
(3)
или
Ln (x)= 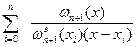 f (xi)
f (xi)
где
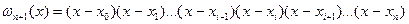 ,
,
 .
.
Теорема. Задача интерполяции всегда имеет единственное решение, которое может быть представлено формулой (3).
Пример 9. Пользуясь формулой Лагранжа, составить интерполяционный многочлен по условиям примера 7. В этом случае 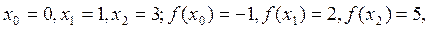
Формула (3) даёт:
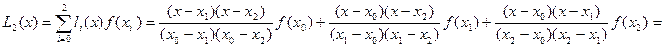
 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 673; Нарушение авторских прав?; Мы поможем в написании вашей работы!