
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод итераций. Уравнение следует привести к виду
|
|
|
|
Уравнение  следует привести к виду
следует привести к виду 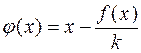 . Итерационный процесс сходится при условии
. Итерационный процесс сходится при условии 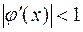 на
на 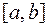 .
.
Это требование накладывает ограничения на выбор величины k.
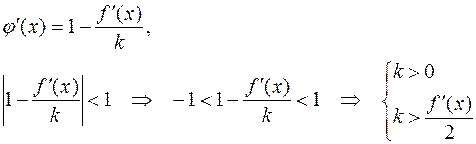
Таким образом, k следует выбирать так, чтобы 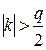 ,
, 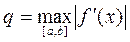 и знак k совпадал бы со знаком
и знак k совпадал бы со знаком 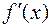 на
на 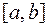 .
.
Уточнение корня производится по формуле 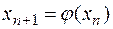 , где
, где 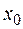 - значение, взятое из промежутка
- значение, взятое из промежутка 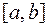 .
.
Точность вычисления можно оценить из соотношения
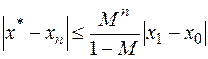 , где
, где 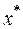 - точное значение корня,
- точное значение корня, 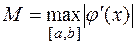
Теорема
Если функция φ (x) удовлетворяет следующим условиям:
1. φ (x) определена и непрерывна на отрезке [ a,b ];
2. φ (x) 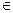 [ a,b ], для
[ a,b ], для 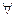 x
x 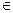 [ a,b ];
[ a,b ];
3. 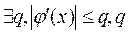 <1,
<1, 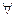 x
x 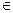 [ a,b ], то уравнение x= φ (x) имеет на отрезке [ a,b ] единственный корень и последовательность{ xn }сходится к этому корню независимо от начального значения.
[ a,b ], то уравнение x= φ (x) имеет на отрезке [ a,b ] единственный корень и последовательность{ xn }сходится к этому корню независимо от начального значения.
Пример. Отделить корни аналитически и уточнить их методом итераций с точностью до 0,001.
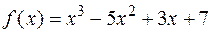
Отделим корни аналитически, для этого найдем критические точки функции, т. е. точки, в которых производная функции обращается в ноль и границы интервала, определим знак функции в них.
Производная 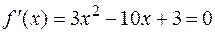 в точках
в точках 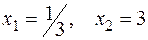 .
.
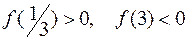
Составим таблицу знаков
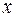
| -∞ | 1/3 | +∞ | |
| Sign f(x) | - | + | - | + |
Так как наблюдается перемена знака функции, то уравнение имеет три действительных корня. Уменьшаем промежутки, содержащие корни.
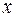
| -1 | 1/3 | 3,7 | |
| Sign f(x) | - | + | - | + |
Следовательно, корни следует искать на промежутках [-1;1/3], [1/3;3], [3;3.7].
Найдем корень на промежутке [-1;1/3]. Составим выражение
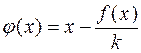 , подобрав значение k таким, чтобы обеспечить сходимость итерационного процесса на данном промежутке. Для этого вычислим значение производной на концах отрезка
, подобрав значение k таким, чтобы обеспечить сходимость итерационного процесса на данном промежутке. Для этого вычислим значение производной на концах отрезка 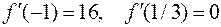 . Тогда
. Тогда 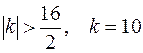
В этом случае
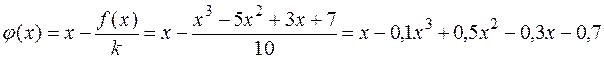
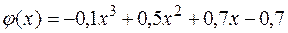
Пусть 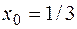 , тогда уточненное значение корня
, тогда уточненное значение корня 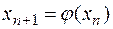 . Вычисления приведены в таблице.
. Вычисления приведены в таблице.
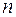
| 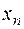
| 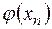
|
| 0,333 | -0,415 | |
| -0,415 | -0,897 | |
| -0,897 | -0,853 | |
| -0,853 | -0,871 | |
| -0,871 | -0,864 | |
| -0,864 | -0,867 | |
| -0,867 | -0,866 | |
| -0,866 | -0,866 | |
| -0,866 | -0,866 |
На промежутке [-1;1/3] найден корень 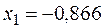 .
.
Теперь рассмотрим промежуток [1/3;3]. На границах этого отрезка  значения производной равны нулю
значения производной равны нулю  , а внутри отрезка
, а внутри отрезка 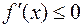 для всех значений
для всех значений 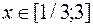 . Вторая производная
. Вторая производная 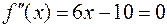 в точке
в точке 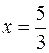 , значение первой производной в этой точке
, значение первой производной в этой точке 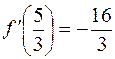 , тогда значение
, тогда значение 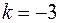 обеспечит сходимость итерационного процесса.
обеспечит сходимость итерационного процесса.
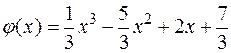 ,
, 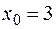 .
.
Вычисления приведены в таблице
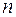
| 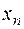
| 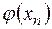
|
| 3,000 | 2,333 | |
| 2,333 | 2,160 | |
| 2,160 | 2,236 | |
| 2,236 | 2,199 | |
| 2,199 | 2,217 | |
| 2,217 | 2,208 | |
| 2,208 | 2,212 | |
| 2,212 | 2,210 | |
| 2,210 | 2,211 | |
| 2,211 | 2,211 | |
| 2,211 | 2,211 |
На промежутке [1/3;3] найден корень 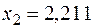 .
.
Рассмотрим отрезок [3;4], значение производной на концах отрезка  , можно взять
, можно взять 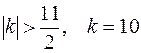 , тогда
, тогда
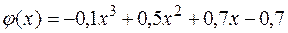 ,
, 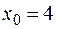 .
.
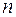
| 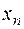
| 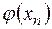
|
| 4,000 | 3,700 | |
| 3,700 | 3,670 | |
| 3,670 | 3,660 | |
| 3,660 | 3,657 | |
| 3,657 | 3,656 | |
| 3,656 | 3,656 | |
| 3,656 | 3,656 |
На промежутке [3;4] найден корень 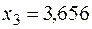 .
.
Пример Решить уравнение 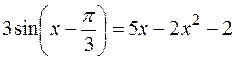 , корни отделить графически.
, корни отделить графически.
Для отделения корней строим графики функций 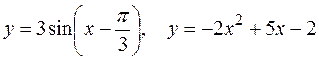 , точки пересечения этих графиков являются корнями заданного уравнения (рис. 1).
, точки пересечения этих графиков являются корнями заданного уравнения (рис. 1).
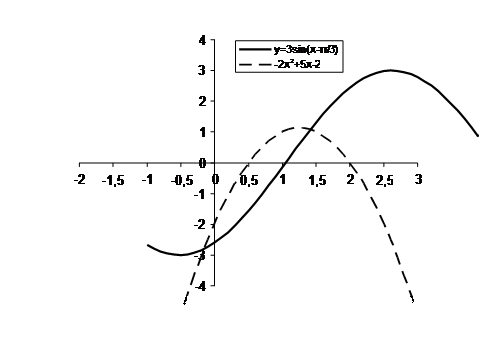
Рис.1.
На графике видно, что уравнение имеет два корня на интервалах [-0,5;0] и [1;1,5]. Уточним эти корни с помощью изученных ранее методов. Результаты использования метода половинного деления на интервале [-0,5;0] приведены в таблице
| 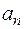
| 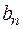
| 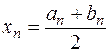
| 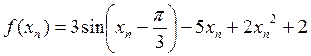
| |
| -0,5000 | 0,0000 | -0,2500 | 0,4870 | ||
| -0,2500 | 0,0000 | -0,1250 | -0,1079 | ||
| -0,2500 | -0,1250 | -0,1875 | 0,1762 | ||
| -0,1875 | -0,1250 | -0,1563 | 0,0308 | ||
| -0,1563 | -0,1250 | -0,1407 | -0,0393 | ||
| -0,1563 | -0,1407 | -0,1485 | -0,0042 | ||
| -0,1563 | -0,1485 | -0,1524 | 0,0134 | ||
| -0,1524 | -0,1485 | -0,1505 | 0,0045 | ||
| -0,1505 | -0,1485 | -0,1495 | 0,0003 | ||
| -0,1495 | -0,1485 | -0,1490 | -0,0020 | ||
| -0,1495 | -0,1490 | -0,1493 | -0,0009 | ||
| -0,1495 | -0,1493 | -0,1494 | -0,0002 | ||
| -0,1495 | -0,1494 | -0,1495 | 0,0000 |
В результате найден корень 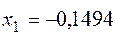 . Аналогично на интервале [1;1,5] ищется корень
. Аналогично на интервале [1;1,5] ищется корень 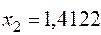 :
:
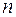
| 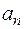
| 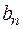
| 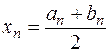
| 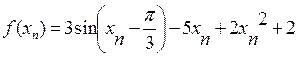
|
| 1,0000 | 1,5000 | 1,2500 | -0,5192 | |
| 1,2500 | 1,5000 | 1,3750 | -0,1264 | |
| 1,3750 | 1,5000 | 1,4375 | 0,0882 | |
| 1,3750 | 1,4375 | 1,4063 | -0,0205 | |
| 1,4063 | 1,4375 | 1,4219 | 0,0336 | |
| 1,4063 | 1,4243 | 1,4153 | 0,0107 | |
| 1,4063 | 1,4153 | 1,4108 | -0,0049 | |
| 1,4108 | 1,4153 | 1,4131 | 0,0029 | |
| 1,4108 | 1,4131 | 1,4120 | -0,0009 | |
| 1,4120 | 1,4131 | 1,4126 | 0,0012 | |
| 1,4120 | 1,4126 | 1,4123 | 0,0003 | |
| 1,4120 | 1,4123 | 1,4122 | -0,0002 | |
| 1,4122 | 1,4123 | 1,4123 | 0,0001 |
Корни могут быть найдены методом касательных, причем количество итераций, потребовавшихся для отыскания корней, меньше.
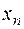
| 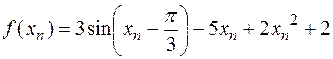
|
| 0,0000 | -0,5973 |
| -0,1707 | 0,0973 |
| -0,1498 | 0,0015 |
| -0,1494 | 0,0000 |
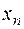
| 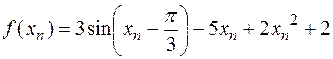
|
| 1,5000 | 0,3139 |
| 1,4151 | 0,0100 |
| 1,4122 | 0,0000 |
Корни данного уравнения найдены: 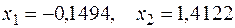
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 451; Нарушение авторских прав?; Мы поможем в написании вашей работы!