
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комбинированный метод хорд и касательных
|
|
|
|
Метод касательных (метод Ньютона).
Mетод состоит в том, что приближение корня ищется как координата точки пересечения касательной с осью О x, проведенной к кривой  в точке
в точке 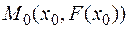 . При этом начальное приближение
. При этом начальное приближение  не требует определения отрезка
не требует определения отрезка 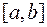 .
.
Уравнение касательной, проходящей через заданную точку к кривой имеет вид:
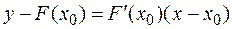 (3)
(3)
Тогда следующее приближение корня определяется как точка пересечения этой касательной с осью абсцисс:
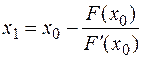 , аналогично для n+1 –го приближения получим
, аналогично для n+1 –го приближения получим  (4), где
(4), где  .
.
В формуле (4)  , если
, если  ;
;  , если
, если 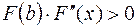 на
на 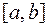 .
.
Для окончания итерационного процесса используется либо условие 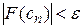 либо условие
либо условие 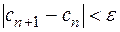 .
.
Пример. Отделить корни аналитически и уточнить их методом касательных с точностью до 0,001.
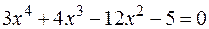
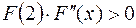 , следовательно, для вычислений применяем формулу
, следовательно, для вычислений применяем формулу  , где
, где  . Вторая производная
. Вторая производная 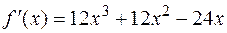
Вычисления представлены в таблице.
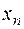
| 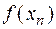
| 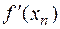
| 
|
| 2,0000 | 27,0000 | 0,28125 | |
| 1,7188 | 6,0404 | 55,12756 | 0,10957 |
| 1,6092 | 0,7100 | 42,456 | 0,01672 |
| 1,5925 | 0,0150 | 40,6721 | 0,00037 |
| 1,5921 | 0,0000 | 40,63327 | 1,8E-07 |
Данные вычислений показывают, что разница между корнями 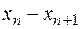 достигает требуемой точности на четвертой итерации. Таким образом, получен корень
достигает требуемой точности на четвертой итерации. Таким образом, получен корень  .
.
Если  и
и  - приближенные значения корня по недостатку и избытку.
- приближенные значения корня по недостатку и избытку.
1. Если 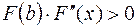 на
на 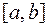 , то
, то
 ,
,  ,
,
при этом 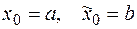 .
.
2. Если 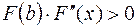 на
на 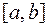 , то
, то
 ,
,

при этом 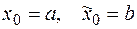 .
.
Пример. Отделить корни аналитически и уточнить их комбинированным методом хорд и касательных с точностью до 0,001.
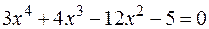
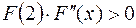 , следовательно, для вычислений применяем формулы
, следовательно, для вычислений применяем формулы
 ,
,

где  - значения корня по недостатку и избытку соответственно,
- значения корня по недостатку и избытку соответственно, 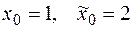 .
.
| x n | F (x n) | 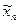
|  F ( F (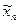 ) )
| 
| 
|  
|
| 1,0000 | -10,0000 | 2,0000 | 27,0000 | 1,0000 | 37,0000 | |
| 1,2703 | -8,3533 | 1,7188 | 6,0404 | 0,4485 | 55,127 | 14,3937 |
| 1,5305 | -2,3064 | 1,6092 | 0,7100 | 0,0786 | 42,456 | 3,0164 |
| 1,5907 | -0,0575 | 1,5925 | 0,0150 | 0,0018 | 40,6721 | 0,0725 |
| 1,5921 | 0,0000 | 1,5921 | 0,0000 | 0,0000 | 40,6332 | 0,0000 |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 732; Нарушение авторских прав?; Мы поможем в написании вашей работы!