Эмпирические формулы и метод наименьших квадратов

Интерполяционная формула Ньютона (для равностоящих узлов)

Используем свойства конечных разностей при выводе формулы Ньютона для равноотстоящих узлов: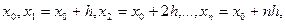

Интерполяционный многочлен может быть представлен любой из следующих формул Ньютона:

а). для интерполирования вперед:

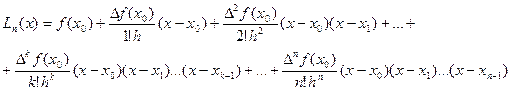(8)

в ). для интерполирования назад:

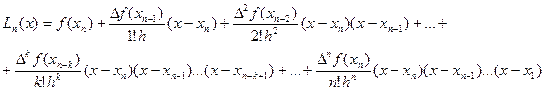(9)

Из единственности интерполяционного многочлена следует, что формулы тождественны. При вычислениях удобнее пользоваться формулой (8) для значений х, близких к начальному значению 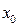, так как при этом основной вклад дают первые слагаемые формулы, а дальнейшие оказываются пренебрежимо малыми. Формулой (9) удобнее пользоваться для значений х, близких к крайнему правому узлу 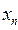. Обе формулы выводятся аналогично, поэтому выведем первую из них (8).

Обозначим через 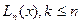интерполяционный многочлен, построенный по узлам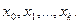

Многочлен 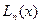можем представить в виде:
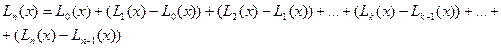(8`)

Разность 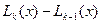является многочленом степени не выше к -й, который обращается в нуль во всех общих для 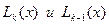узлах интерполяции 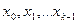. Следовательно, разность может быть представлена в виде:

.

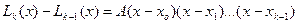Для вычисления коэффициента А используем разность к - того порядка от обеих частей последнего соотношения:

.

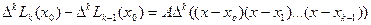По свойству 5 конечных разностей,

.

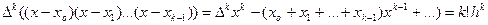По свойству 4, .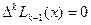

В узлах интерполяции 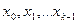значения многочлена 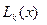совпадают со значениями функции f(x). Значения разности 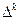определяются узловыми значениями функции, поэтому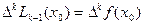

и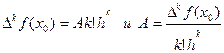

Следовательно, 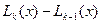= 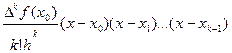, к = 1,2,…,n, .

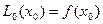Подставляя эти выражения в формулу (8'), получим интерполяционную формулу Ньютона:

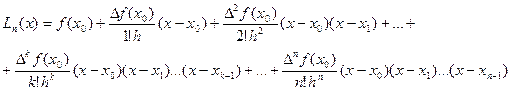
Величины 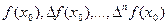, входящие в формулу для интерполирования вперёд, находятся на верхней диагонали таблицы. Аналогичные величины для второй формулы находятся на нижней диагонали (см. таблицу).

Пример 11. Составить интерполяционные формулы Ньютона по приведённой таблице.

x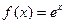
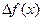
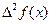
1,00	2,7183	0,2859 0,3159	0,0300
1,10	3,0042
1,20	3,3201

Вычислить .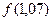

a.) По формуле (8) для интерполирования вперёд:

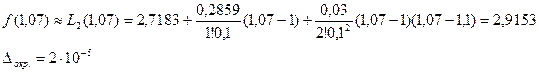
b.) По формуле (9) для интерполирования назад:

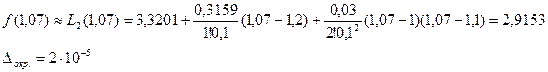
3.8. Погрешность формулы Ньютона.

Полная погрешность формулы Ньютона по общему правилу выражается формулой:

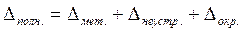
Вычислим устранимую и неустранимую погрешности метода. Оценим разность 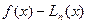. Интерполяционный многочлен Ньютона тождественно совпадает с многочленом Лагранжа, построенным по тем же узлам, следовательно, остаётся неизменной оценка:

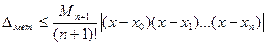
Неустранимая погрешность возникает при вычислении разностей 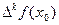, вместо точных значений 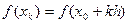используются приближённые значения 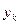. Погрешность приближённых значений 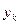обозначим:

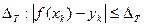
Используя формулу (8), видим, что

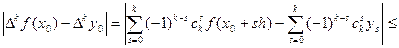
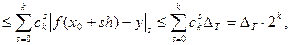так как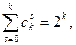

Если 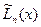многочлен Ньютона, построенный по приближённым значениям 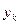, то

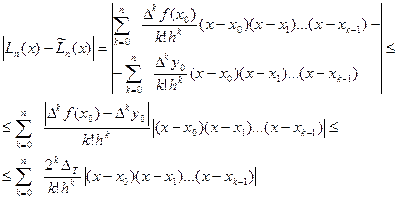
Таким образом,

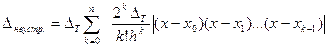
Пример 12. Оценить погрешность вычисления в примере 10.

Имеем, 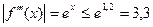, т.е., 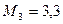. Следовательно,

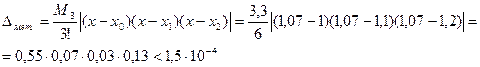
Далее, 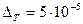и, следовательно,

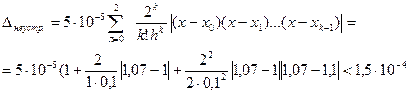
Таким образом,

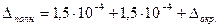
Если округлить, полученные в примере 10 значения 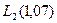до четырёх верных знаков после запятой, то .

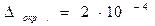Тогда .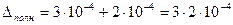

Следовательно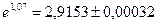

3.9. Интерполяционные сплайны. Параболические интерполяционные сплайны

Для уменьшения погрешности интерполирования (погрешности метода) необходимо использовать многочлены высокой степени, что приводит к увеличению неустранимой погрешности и погрешности округления и невысокой точности интерполяционных формул.

Рассмотрим способ приближения функций, основанный на разбиении отрезка; отрезок, на котором нужно приблизить функцию, разбивается на части, на каждой из которых функция достаточно точно приближается многочленом невысокой степени.

Для приближённого представления функции f(x) на отрезке 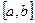выберем на нём две системы узлов:

а) узлы 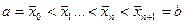, называемые узлами сплайна.

в) узлы 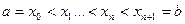, называемые узлами интерполяции.

Узлы выбираем так, что для i=1,2,…,n-1 имеем , т.е. между двумя внутренними узлами сплайна лежит один узел интерполяции.

Функция 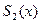называется параболическим интерполяционным сплайном для функции f(x), построенным по указанным узлам, если:

1.Функция 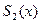и её производная 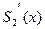непрерывны на отрезке .

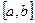2. На каждом отрезке 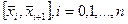между двумя последовательными узлами сплайна функция 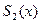является многочленом второй степени:

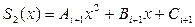для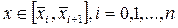

3. В узлах интерполяции значения сплайна 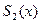совпадают со значениями функции f(x).

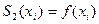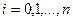, для n=2.

Запишем систему условий, определяющих параболический интерполяционный сплайн :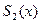

a) условия интерполяции

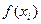
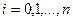= (1)

Так как узел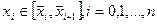

b) условия непрерывности сплайна в узлах сплайна.

В каждом внутреннем узле сплайна 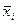стыкуются два участка 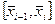и 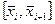. На первом из них сплайн 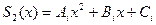, а на втором 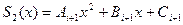. Условие непрерывности в точке 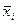даёт

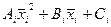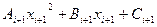= (2)

с) условия непрерывности производной 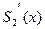во внутренних узлах сплайна приводят к соотношениям 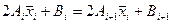, 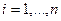(3)

Узлы сплайна разбивают весь отрезок на (n+1) частей, на каждой из которых сплайн определяется тремя коэффициентами 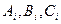, поэтому необходимо определить 3(n+1)=3n+3 неизвестных коэффициентов.

Указанные выше условия (1),(2),(3) содержат соответственно n+1, n и n уравнений. Число неизвестных на 2 превосходит число уравнений. Для того, чтобы система имела лишь одно решение, нужно добавить ещё два условия.

1. Если функция f(x) периодическая с периодом Т=b-a,то должно выполняться условие периодичности производных сплайна:

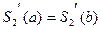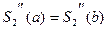и (4)

В развёрнутом виде: .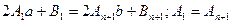

3. В крайних узлах сплайна должны совпадать значения первых производных сплайна и функции:

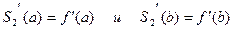,т.е.

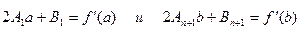(5)

Можно доказать, что система уравнений (1)-(3), дополненная условиями (4) или (5), имеет единственное решение.

Приведём оценки погрешности, возникающей при замене функции f(x) её параболическим сплайном 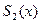для случая, когда внутренние узлы сплайна расположены точно посередине между узлами интерполяции, т.е. 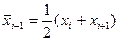и предположим, что f(x) имеет ограниченную производную третьего порядка 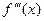на отрезке .

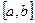При выполнении указанных дополнительных условий (4) или (5) справедливы оценки:

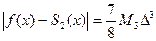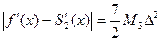, для любого 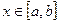, (6)

где 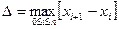, 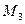-верхняя граница значений 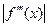на отрезке .

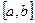Из оценок (6) следует, что при 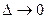, значения сплайна и его производной стремятся соответственно, к значению функции и её производно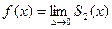й:

и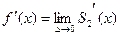

Получена погрешность метода f(x)-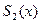

Неустранимую оценку погрешности вычислять не будем.

Пример 13.

На отрезке 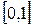выбраны:

А) узлы сплайна: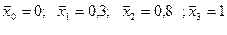

В) узлы интерполяции: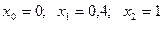

Найти параболический сплайн 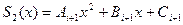, 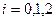для функции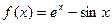

Составим систему уравнений, определяющих параболический сплайн :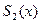

1)Условия интерполяции: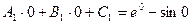

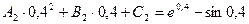
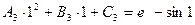
2)Условия непрерывности 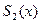во внутренних узлах сплайна:

;

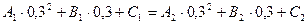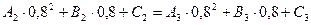
3)Условия непрерывности производной 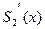во внутренних узлах сплайна:

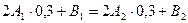
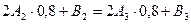
4)Дополнительное условие: в крайних узлах сплайна значение его производной совпадает со значением производной функции:

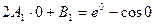
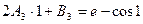
Взяв из таблиц значение функции 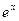,sinx для указанных значений аргумента, получим:

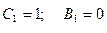
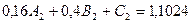
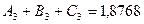
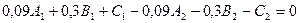
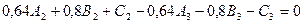
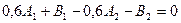
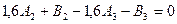
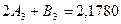
Решая систему получим:

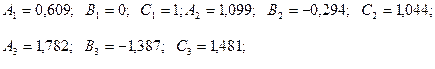
Следовательно, сплайн 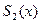определяется следующим образом:

=

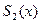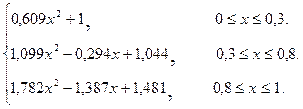
Приближённое представление функций с помощью интерполяционных многочленов и сплайнов имеет смысл при условии, что значение приближаемой функции известны достаточно точно (т.е. при малых 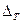). В противном случае, неустранимая погрешность настолько велика, что бессмысленно добиваться высокой теоретической точности метода. Использование интерполяционных многочленов и сплайнов при значительном числе узлов приводит к громоздким выражениям.

В тех случаях, когда значения функции определены с невысокой точностью и необходимо составить приближенное аналитическое выражение, прибегают к эмпирическим формулам: несложным формулам определенного типа. Задача состоит в выборе вида формулы, хорошо отражающей имеющиеся данные и определении её параметров.

Функция задана таблично:

			…
			…

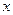
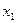
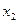
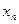
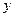
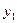
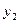
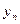
Требуется найти функциональную зависимость в виде: 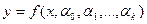(1)

где 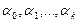неизвестные параметры.

Используются, например, формулы вида: 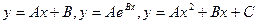и т.п.,

Параметры формул естественно стремятся определить так, чтобы отклонения 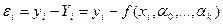были по возможности меньшими.

Требовать обращение в нуль всех 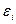нельзя, так как это приведёт к системе, содержащей гораздо больше уравнений, чем неизвестных(n уравнений при к неизвестных, где k<n). В соответствии с общей схемой вводится некоторая числовая мера близости значений 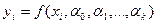к табличным значениям.

Например, можно ввести меры:

;

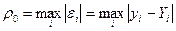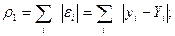
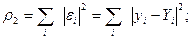
Каждая из введённых мер является функцией параметров

:

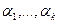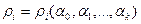
Малость каждой из них эквивалентна малости величины .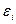

Параметры 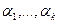определяются из условий минимума соответствующей мера. Наиболее употребительной является мера

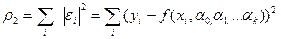(2)

Метод, определяющий параметры эмпирической формулы из условия минимума величины 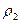, называется методом наименьших квадратов.

Из необходимых условий минимума функции нескольких переменных 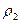следует, что в точке минимума градиент функции равен нулю.

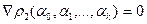(3)

т.е.в точке минимума равны нулю все её частные производные первого порядка:

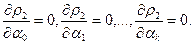(4)

Для следующих эмпирических формул:

a)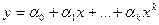

b)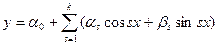

c)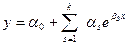

Система уравнений (4) имеет единственное решение 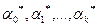и при этом функция 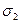принимает наименьшее значение: для любых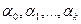

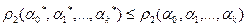
В других случаях нужно дополнительное исследование решений системы (4).

В качестве примера рассмотрим случай приближения с помощью линейной функции .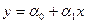

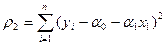. Необходимые условия минимума приводят к системе двух уравнений:

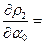
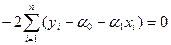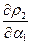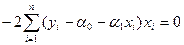, = (5)

После преобразований, получим:

,

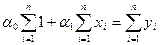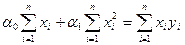
Так как 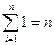, то приходим к системе

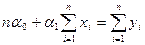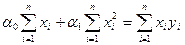, (6)

Определитель этой системы

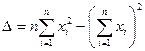можно представить в виде .

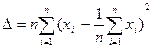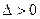всегда за исключением лишь случая, когда все принимают одно и тоже значение. Система(6) всегда имеет единственное решение, которое находится по формулам Крамера:

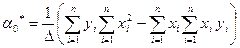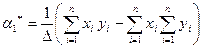; (7)

Функция 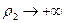при 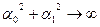, поэтому принимает наименьшее значение в точке с конечными координатами, причём точка обязательно является точкой минимума функции 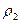. Функция 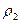имеет единственный экстремум 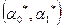, в которой функция 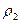принимает наименьшее значение.

Замечание. Соотношение (5) показывает, что для решения системы должно быть выполнено соотношение:

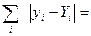
которое можно использовать для контроля вычислений.

Заметим, что для определения коэффициентов аппроксимирующей функции в виде многочлена получается система:

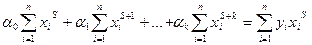
Пример 14.

Требуется определить зависимость скорости течения V от относительной глубины D по результатам десяти наблюдений приведённых в таблице.

									-
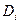
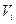
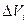
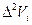
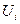
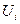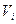
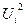
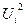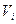
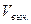
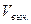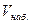
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
	0,957	0,012	-0,005	-9	-8,613		77,517	0,957
0,1	0,969		-5	-7	-6,783		47,481	0,969
0,2	0,976		-5	-5	-4,880		24,400	0,976
0,3	0,978	-3	-4	-3	-2,934		8,802	0,979	0,001
0,4	0,975	-7	-7	-1	-0,975		0,975	0,976	0,001
0,5	0,968	-14	-1		0,968		0,968	0,969	0,001
0,6	0,954	-15	-6		2,862		8,586	0,957	0,003
0,7	0,939	-21	-3		4,695		23,475	0,940	0,001
0,8	0,918	-24			6,426		44,982	0,919	0,001
0,9	0,894				8,046		72,414	0,892	-0,002
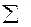
	9,528				-1,188		309,600

Для определения степени аппроксимирующего многочлена рассмотрим в столбцах (3),(4) разности. Вторые разности (4) практически постоянные, поэтому необходимо выбрать аппроксимирующий многочлен второй степени.

V=a₀+a₁D+a₂D²,

коэффициенты a_{0 ,} a₁, a_2, найдем из системы метода наименьших квадратов

10 a₀ +4,5 a₁ +2,85 a₂ =9,528,

4,5 a₀ +2,85 a₁ +2,025 a₂ =4,228,

2,85 a₀ +2,025 a₁ + 1,533 a₂ =2,65,

Решив систему уравнений получим: a₀ =0,958, a₁= 0,134, a₂ =0,228.

Искомая зависимость имеет вид:

V= 0,958 + 0,134 D+ 0,228 D²

Глава 4. Численное дифференцирование и интегрирование

Приближенное дифференцирование применяется в случаях, когда необходимо найти производную функции 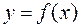, заданной табличным способом либо в случаях, когда аналитическое выражение настолько сложное, что непосредственное дифференцирование функции затруднено. Допустим необходимо продифференцировать функцию 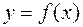на отрезке 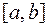. Заменим заданную функцию 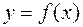интерполирующей функцией 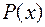, при этом 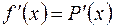для всех значений 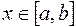. Интерполирование функций можно производить с помощью различных способов.

Дата добавления: 2014-12-27