
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула трапеций. Вычислим коэффициенты Котеса при
|
|
|
|
Вычислим коэффициенты Котеса при 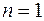 .
.
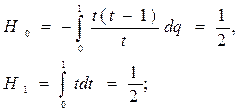
Значения коэффициентов удовлетворяют условиям (7), следовательно, используя квадратурную формулу (6) получим следующую формулу для вычисления определенного интеграла
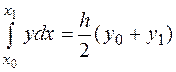 (8).
(8).
Формула (8) называется формулой трапеций для приближенного вычисления определенного интеграла. Остаточный член (ошибка) квадратурной формулы (8) равен
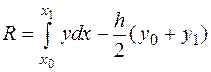 (9).
(9).
Если 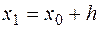 , то
, то 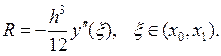 (10)
(10)
Для вычисления интеграла 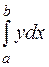 можно разделить промежуток интегрирования на
можно разделить промежуток интегрирования на 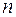 равных частей
равных частей  и к каждому из них применить формулу трапеций (8). Полагая,
и к каждому из них применить формулу трапеций (8). Полагая, 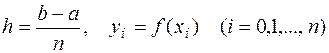 получим
получим
 . (16)
. (16)
Геометрический смысл формулы (16) состоит в том, что график подынтегральной функции 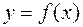 заменяется ломаной линией.
заменяется ломаной линией.
Ошибка общей формулы трапеций (16) составляет
 (17)
(17)
Пример.
Вычислить интеграл по формуле трапеций с тремя десятичными знаками.

Для достижения требуемой точности необходимо определить количество точек разбиения n, удовлетворяющее условию
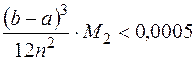 , где
, где 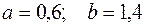 - пределы интегрирования,
- пределы интегрирования, 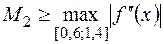 , где
, где 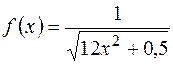 .
.
Находим производные

Оценим максимальное значение второй производной на отрезке интегрировании, для этого в числитель подставим верхний предел, в знаменатель – нижний:

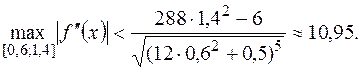
Пусть  , тогда
, тогда 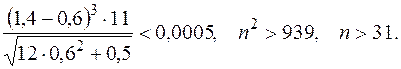 Возьмем
Возьмем 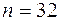 . Результат вычислений приведен в таблице.
. Результат вычислений приведен в таблице.
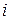
| 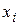
| 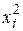
| 
| 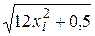
| 
|
| 0,6000 | 0,3600 | 4,8200 | 2,1954 | 0,4555 | |
| 0,6250 | 0,3906 | 5,1875 | 2,2776 | 0,4391 | |
| 0,6500 | 0,4225 | 5,5700 | 2,3601 | 0,4237 | |
| 0,6750 | 0,4556 | 5,9675 | 2,4428 | 0,4094 | |
| 0,7000 | 0,4900 | 6,3800 | 2,5259 | 0,3959 | |
| 0,7250 | 0,5256 | 6,8075 | 2,6091 | 0,3833 | |
| 0,7500 | 0,5625 | 7,2500 | 2,6926 | 0,3714 | |
| 0,7750 | 0,6006 | 7,7075 | 2,7762 | 0,3602 | |
| 0,8000 | 0,6400 | 8,1800 | 2,8601 | 0,3496 | |
| 0,8250 | 0,6806 | 8,6675 | 2,9441 | 0,3397 | |
| 0,8500 | 0,7225 | 9,1700 | 3,0282 | 0,3302 | |
| 0,8750 | 0,7656 | 9,6875 | 3,1125 | 0,3213 | |
| 0,9000 | 0,8100 | 10,2200 | 3,1969 | 0,3128 | |
| 0,9250 | 0,8556 | 10,7675 | 3,2814 | 0,3047 | |
| 0,9500 | 0,9025 | 11,3300 | 3,3660 | 0,2971 | |
| 0,9750 | 0,9506 | 11,9075 | 3,4507 | 0,2898 | |
| 1,0000 | 1,0000 | 12,5000 | 3,5355 | 0,2828 | |
| 1,0250 | 1,0506 | 13,1075 | 3,6204 | 0,2762 | |
| 1,0500 | 1,1025 | 13,7300 | 3,7054 | 0,2699 | |
| 1,0750 | 1,1556 | 14,3675 | 3,7904 | 0,2638 | |
| 1,1000 | 1,2100 | 15,0200 | 3,8756 | 0,2580 | |
| 1,1250 | 1,2656 | 15,6875 | 3,9607 | 0,2525 | |
| 1,1500 | 1,3225 | 16,3700 | 4,0460 | 0,2472 | |
| 1,1750 | 1,3806 | 17,0675 | 4,1313 | 0,2421 | |
| 1,2000 | 1,4400 | 17,7800 | 4,2166 | 0,2372 | |
| 1,2250 | 1,5006 | 18,5075 | 4,3020 | 0,2324 | |
| 1,2500 | 1,5625 | 19,2500 | 4,3875 | 0,2279 | |
| 1,2750 | 1,6256 | 20,0075 | 4,4730 | 0,2236 | |
| 1,3000 | 1,6900 | 20,7800 | 4,5585 | 0,2194 | |
| 1,3250 | 1,7556 | 21,5675 | 4,6441 | 0,2153 | |
| 1,3500 | 1,8225 | 22,3700 | 4,7297 | 0,2114 | |
| 1,3750 | 1,8906 | 23,1875 | 4,8153 | 0,2077 | |
| 1,4000 | 1,9600 | 24,0200 | 4,9010 | 0,2040 |
Значение интеграла вычисляем по формуле

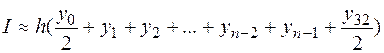 ,
,
где 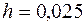 .
.
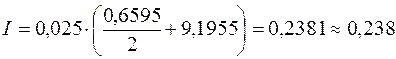 .
.
Для проверки полученного результата вычислим данный интеграл с помощью формулы Ньютона – Лейбница.

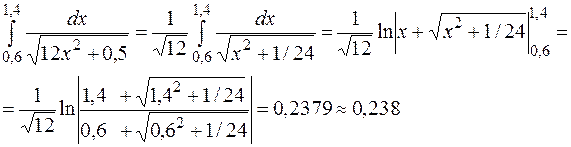
Результат вычислений показывает, что формула трапеций дает значение, совпадающее до третьего знака после запятой с точным значением.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 607; Нарушение авторских прав?; Мы поможем в написании вашей работы!