Формула Симпсона (формула парабол)

Для получения формулы Симпсона коэффициенты Котеса (5) вычисляются при .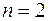

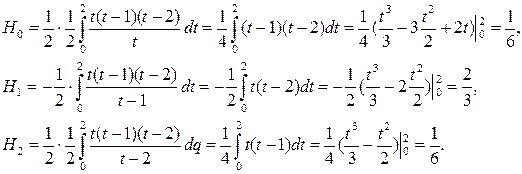(11)

В результате квадратурная формула примет вид

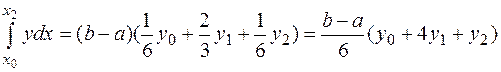(12)

Учитывая, что 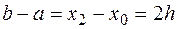получим формулу Симпсона для приближенного интегрирования

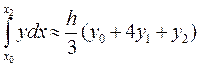(13)

Геометрический смысл формулы Симпсона состоит в том, что в кривая 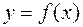заменяется параболой 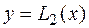, проходящей через три точки .

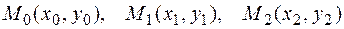Остаточный член формулы Симпсона равен

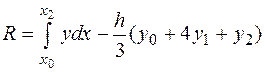
Зафиксируем среднюю точку 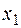, и запишем выражение для остаточного члена, как функции от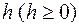

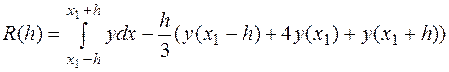(14)

Остаточный член формулы Симпсона равен

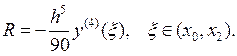(15)

Формула Симпсона имеет повышенную точность для многочленов второй и третьей степени.

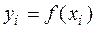Пусть есть четное число и значения функции в равноотстоящих точках 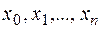с шагом 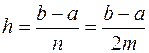. Применяя формулу Симпсона (13) к каждому удвоенному промежутку длины 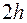получим

.

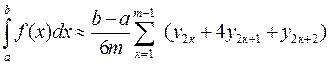После преобразования правой части получим формулу Симпсона в виде удобном для вычислений

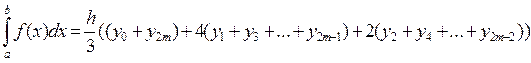(18)

Погрешность вычисления при использовании формулы Симпсона

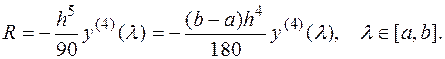
Пример. Вычислить интеграл I= 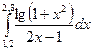по формуле Симпсона при n =10 и оценить погрешность результата с помощью таблицы конечных разностей.

Вычислим шаг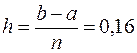

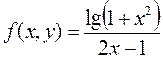- подынтегральная функция.

Значения подынтегральной функции

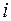
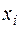
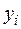
	1,20	0,2767
	1,36	0,2644
	1,52	0,2548
	1,68	0,2468
	1,84	0,2396
	2,00	0,2330
	2,16	0,2269
	2,32	0,2212
	2,48	0,2157
	2,64	0,2106
	2,80	0,2058

Значение интеграла вычисляем по формуле:

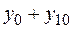
	0,4825
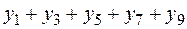
	1,1759
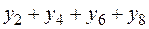
	0,9370
Значение интеграла	0,3765

Для оценки точности полученного результата составим таблицу конечных разностей функции до разностей четвертого порядка

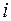
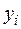
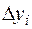
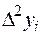
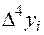
	0,2767	-0,01230	0,00273	-0,00126	0,00068
	0,2644	-0,00957	0,00148	-0,00057	0,00029
	0,2548	-0,00809	0,00090	-0,00028	0,00013
	0,2468	-0,00719	0,00062	-0,00015	0,00006
	0,2396	-0,00657	0,00046	-0,00009	0,00003
	0,2330	-0,00611	0,00038	-0,00005	0,00002
	0,2269	-0,00573	0,00032	-0,00004	0,00001
	0,2212	-0,00541	0,00029	-0,00003
	0,2157	-0,00512	0,00026
	0,2106	-0,00487

Из таблицы следует, что 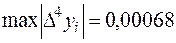, тогда остаточный член, определяющий погрешность вычислений, будет равен

.

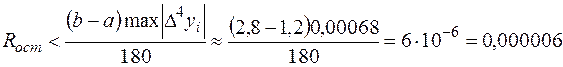Требование к точности вычисления ограничивается четырьмя знаками после запятой, остаточный член на два порядка меньше, следовательно, необходимая точность вычислений достигнута.

5.4. Формулы Ньютона – Котеса высших порядков

Производя соответствующе вычисления при 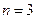можно получить квадратурную формулу Ньютона – Котеса с четырьмя ординатами,

,

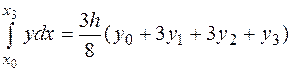при 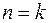будет, соответственно, получена квадратурная формула k-го порядка с (k+1) ординатами. В таблице приведены коэффициенты Котеса для разного количества ординат.

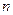
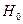
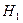
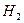
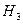
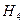
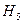
	1/2	1/2
	1/6	2/3	1/6
	1/8	3/8	3/8	1/8
	7/90	16/45	2/15	16/45	7/90
	19/288	25/96	25/144	25/144	25/96	19/288

Пример. Вычислить 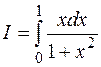, используя формулу Ньютона – Котеса с пятью ординатами (n=4).

Решение. При n=4 шаг равен 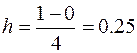. Составим таблицу для вычисления интеграла:

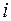
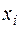
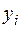
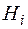
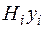
			7/90
	0.25	4/17	16/45	0.08366
	0.5	0.4	4/30	0.05333
	0.75	0.48	16/45	0.17067
		0.5	7/90	0.03889
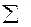
				0.34655

Таким образом, получили значение определенного интеграла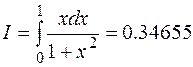

Точное значение интеграла:

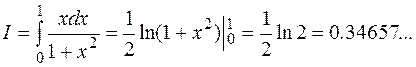
Приближенное значение интеграла отличается от точного в пятом знаке после запятой, т.е. точность вычислений высокая.

Коэффициенты Котеса при большом числе ординат сложны, практически для приближенного вычисления определенных интегралов можно разбить промежуток интегрирования на большое число мелких интервалов и к каждому из них применить квадратурную формулу Ньютона – Котеса с малым числом ординат.

Глава 6. Численное интегрирование обыкновенных дифференциальных уравнений

Обыкновенным дифференциальным уравнением называется уравнение, содержащее одну или несколько производных от искомой функции 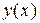: 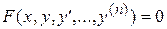, (1)

где x -независимая переменная.

Наивысший порядок производной, входящей в уравнение называется порядком дифференциального уравнения (1). Уравнения первого и второго порядков имеют следующий вид: 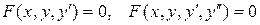(2).

Линейным дифференциальным уравнением называется уравнение линейное относительно искомой функции и ее производных.

Решением дифференциального уравнения (1) называется функция 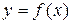, при подстановке которой в уравнение оно превращается в тождество. Общее решение дифференциального уравнения n -го порядка содержит n произвольных постоянных 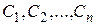. Общее решение уравнения (1) имеет вид: 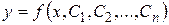, соответственно, уравнения первого и второго порядков - 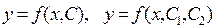. Частное решение получается из общего при определенных значениях произвольных постоянных. Для получения частного решения необходимо наличие начальных условий. Нахождение решения удовлетворяющего начальным условиям называется задачей Коши. Решить задачу Коши – означает найти функцию 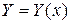, удовлетворяющую уравнению 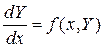и принимающую заданное значение .

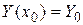Если дополнительные условия задаются более чем в одной точке, то задача называется краевой задачей, дополнительные условия – граничными. Как правило, в качестве граничных условий задаются условия на границах области решения дифференциального уравнения.

Дифференциальное уравнение 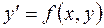в каждой точке плоскости, в которой существует функция 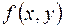, задает направление интегральной кривой уравнения, проходящей через эту точку и тем самым определяет поле направлений. Решить задачу Коши – означает найти решение уравнения 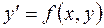, удовлетворяющее заданному начальному условию .

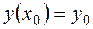Наиболее распространенным и универсальным численным методом решения дифференциальных уравнений является метод конечных разностей. Область непрерывного изменения аргумента заменяется дискретным множеством точек, которые называются узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Замена называется разностной аппроксимацией и решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки.

Дата добавления: 2014-12-27