Методические указания. Работа №1. Метод равномерного поиска

Работа №1. Метод равномерного поиска

Описания к лабораторным работам

Задание

1. Ознакомиться с алгоритмом машинного метода одномерной оптимизации равномерного поиска.

2. Составить программу метода и отладить на контрольном примере.

3. Рассчитать экстремум функции, заданной по варианту, и сопоставить точку экстремума с точкой минимума на графике функции.

4. Произвести расчет экстремум функции для двух различных значений точности.

5. Модифицировать метод равномерного поиска, введя переменный шаг.

6. Сравнить скорость сходимости метода равномерного поиска с постоянным и переменным шагом.

1. Среди одномерных методов поиска экстремума целевой функции наиболее простыми является метод равномерного поиска. Описание метода приведено в разделе 3, тема3.

Названный метод требует задания целевой функции F(х) и начального интервала (a,b), на котором заданная функция унимодальна. Алгоритм позволяет уменьшить начальный интервал до некоторого конечного (х _1, х ₂ ) < δ, где δ – заданная точность.

Блок-схема машинного алгоритма метода равномерного поиска приведена на рис. 22. В качестве машинных переменных, соответствующих текущему значению параметра оптимизации на i -ом и (i+1)- ом шаге использованы идентификаторы х и х ₁, а для значений целевой функции F, F ₁ соответственно. Оптимальное значение параметра по завершении расчета содержится в х, целевой функции в F.

Нет

Да

Если х < ,b, то идти к 3

Нет

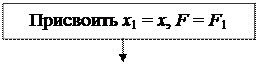Да

Рис. 23. Блок-схема алгоритма метода равномерного поиска.

2. На основании блок-схемы алгоритма составляется программа в Mathcad. Текст программы и отладочный пример приведены на рис. 24 (скриншот).

Входными данными программы являются целевая функция F(х), начальный интервал (a,b) и δ – точность по параметру оптимизации.

Программа вводится согласно правилам, приведенным в разделе 4. Далее производится отладка программы на примере целевой функции и параметров, приведенных на рис. 23. Там же построен график целевой функции F (х) для отладочного примера, который демонстрирует, что данная функция унимодальна на заданном интервале (а, в).

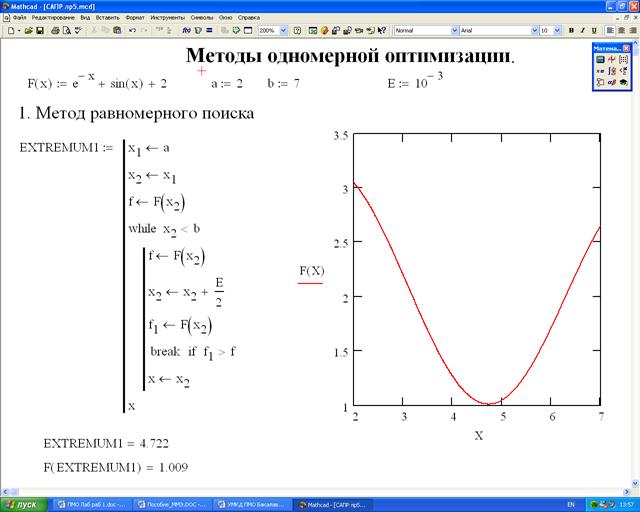
Рис. 24. Программная реализация метода равномерного поиска в Mathcad.

3. Для выполнения задания нужно ввести в программу функцию, соответствующую варианту задания и заданному интервалу, и произвести расчет точки экстремума с заданной точностью. Варианты целевых функций, а также значения параметров для расчетов согласно вариантам заданий приведены в таблице 3.

Таблица 3. Варианты заданий

Номер варианта	Целевая функция F (x)	Интервал (а,b)	Точность e
	4 – 0,1 х + cos(x)	0 – 5,0	0,01
	х ² + 1/ х	0,1 – 2,0	0,001
	tg(x) + 1/ х	0,1 – 1,5	0,0001
	exp(x) + 1/ х	0,1 – 1,0	0,001
	tg(x) – ln(x)	0,1 – 1,0	0,0001
	3۰exp(– x) + sin(x)	0 – 8,0	0,01

Рассчитанное значение экстремума функции (точку экстремума) необходимо сопоставить с точкой минимума на графике функции.

4. С целью оценки влияния точности на точку минимума необходимо, уменьшив порядок точности на единицу, произвести расчет экстремума функции и сопоставить значение точки экстремума для двух различных значений точности.

5. Чтобы модифицировать метод равномерного поиска, введя переменный шаг, необходимо ввести в программу формулу расчета шага: h:= 0,1 ۰ k ۰ h, где (для k принять значение номера варианта) и логическую переменную R, значение которой присвоить равным 2, пока выполняется условие F₁ > F, и значение 0,5 – в противном случае.

6. Для того, чтобы сравнить скорость сходимости метода равномерного поиска с постоянным и переменным шагом, нужно вставить в цикл программы счетчик и оценить скорость сходимости по числу циклов.

Дата добавления: 2014-12-27