Логико-вероятностные методы расчета резервированных систем

Существо логико-вероятностных методов расчета надежности состоит в описании схемы системы с помощью аппарата математической логики с последующим использованием теории вероятности при определении характеристик надежности.

Расчет надежности сложного изделия, по существу, является определением истинности сложного высказывания.

Приведем пример высказывания: «изделие находится в работоспособном состоянии, если в работоспособном состоянии находится его элемент а и один из следующих элементов: элемент b, или d, или оба элемента вместе взятых». Такое высказывание является сложным, состоящим из простых высказываний, связанных между собой логическими операциями конъюнкции (связка «и», обозначается знаком 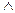) и дизъюнкции (связка «или», обозначается знаком 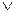)- На языке математической логики оно может быть записано следующим образом:

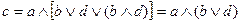
Главное в такой записи состоит не только в том, что существует возможность записать условие работоспособности изделия в виде математической (логической) формулы и преобразовать эту запись, а в том, что такие формулы можно подвергать математической обработке: соединять их в более сложные структуры, разлагать, преобразовывать, оптимизировать, находить по ним значения исследуемых величин, переходить от формул к схемам и наоборот и т.д.

Таким образом, использование аппарата математической логики позволяет формализовать условия работоспособности сложных структур и получать формулы для расчета надежности. Чтобы понять, как все это делается, рассмотрим вначале некоторые самые необходимые шесть положений математической логики.

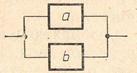
Рисунок 29 – Схема параллельного соединения элементов (операция дизъюнкции)

Рисунок 30 – Схема последовательного соединения элементов (операция конъюнкции)

Рисунок 31 – Схема инвертирования входной величины

1. Если о некотором высказывании C можно утверждать, что оно истинно, если истинны высказывания A или B, тогда делается вывод о том, что высказывание C равно высказываниям A и B, связанным между собой логической операцией дизъюнкции:

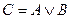
Точно так же, если об изделии можно утверждать, что оно работоспособно, если работоспособен его элемент а или b, можно сделать вывод о том, что работоспособность изделия (событие с) и работоспособности элементов а или b (событие а и событие b) связаны между собой логическим уравнением работоспособности:

Логическая операция дизъюнкции может быть представлена схемой параллельного соединения элементов а и b (рис. 29).

2. Если о некотором высказывании C можно утверждать, что оно истинно тогда, когда истинны высказывания A и B, то делается вывод о том, что высказывание C равно высказываниям A и B, связанным между собой логической операцией конъюнкции:

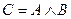
Точно так же, если об изделии можно утверждать, что оно работоспособно, если работоспособны элемент а и элемент b, можно сделать вывод о том, что работоспособность изделия (событие с) и работоспособности элементов а и b (событие а и событие b) связаны между собой логическим уравнением работоспособности:

Логическая операция конъюнкции может быть представлена схемой последовательного соединения элементов а и b (рис. 30).

3. Если некоторое высказывание A отрицается высказыванием b, тогда говорят, что высказывание A и высказывание B связаны между собой логической операцией отрицания:

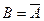
Эта формула читается так: B есть не A.

В теории надежности она может, например, найти такое применение. Если работоспособное состояние элемента a обозначить а, то неработоспособное состояние элемента a обозначается .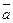

На рис. 31 изображено устройство (инвертор), преобразующее высказывание A в высказывание не А. Таким устройством может быть устройство, преобразующее «1» в «0», в схеме расчета надежности – переход в отказное состояние.

4. Логические операции дизъюнкции, конъюнкции и отрицания – основные операции, используемые в прикладной теории надежности, так как к ним могут быть сведены все другие логические операции.

5. Сложную логическую функцию можно минимизировать, т. е. преобразовать ее таким образом, что она будет содержать наименьшее число членов или в ней не будет повторяющихся членов.

Для минимизации функций и для исключения повторяющихся членов рекомендуются следующие формулы:

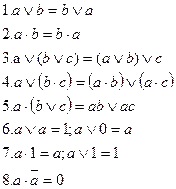
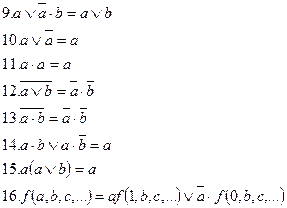
Преобразование логической функции к такому виду, когда в ней нет повторяющихся членов, совершенно необходимо при расчетах надежности. Если функция имеет вид 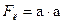(а – событие), то ее нельзя непосредственно использовать для расчета вероятности сложного события. Замена событий вероятностями приведет к формуле 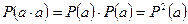. На самом же деле 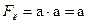. Поэтому .

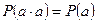Особого внимания заслуживает формула разложения F_л на две составляющие. Она используется тогда, когда все остальные формулы не позволяют исключить повторяющиеся члены.

6. Логические функции можно преобразовать в функции алгебраические, если заменить все логические операции арифметическими по следующим правилам:

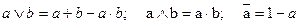
Логическую функцию работоспособности, у которой все логические операции заменены арифметическими, будем называть функцией работоспособности, представленной в арифметическом виде.

Последовательность расчета надежности. Чтобы получить формулу для вероятности работоспособного состояния сложного изделия, необходимо:

1) сформулировать словесно условие работоспособности изделия;

2) на основании формулировки об условии работоспособности изделия записать логическую функцию работоспособности F_л;

3) преобразовать в случае необходимости логическую функцию работоспособности (минимизировать, исключить повторяющиеся члены);

4) в логической функции работоспособности заменить логические операции арифметическими, т. е. получить F_а;

5) в арифметической функции работоспособности заменить простые события (простые высказывания) их вероятностями;

6) в полученную формулу, устанавливающую связь между вероятностями состояний элементов изделия и вероятностью состояния сложного изделия, подставить числовые значения вероятностей состояний элементов. Решением полученного уравнения определить числовое значение вероятности работоспособного состояния сложного изделия

Последовательность логико-вероятностного метода расчета надежности систем следующая:

1) словесная формулировка условий работоспособности системы;

2) составление логической функции работоспособности;

3) минимизация F_л и приведение к бесповторной форме;

4) арифметизация F_л;

5) замена событий (высказываний) их вероятностями;

6) расчет надежности (определение 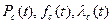и других характеристик);

7) анализ полученных результатов.

Дата добавления: 2014-12-27