
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение преобразований
|
|
|
|
Часто в геометрических задачах приходится иметь дело не с одним преобразованием, а с последовательным выполнением двух и более преобразований. Результат последовательного выполнения преобразований называется произведением, или умножением, или композицией преобразований.
Сказанное можно представить в виде схемы (рисунок 1.9):
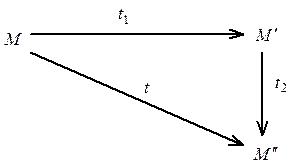 |
Рисунок 1.9 – Наглядное представление произведения преобразований
Здесь представлено два преобразования  и
и  плоскости, выполненные последовательно. Сначала выполняется преобразование
плоскости, выполненные последовательно. Сначала выполняется преобразование  , переводящее точку
, переводящее точку  (прообраз первого преобразования) в точку
(прообраз первого преобразования) в точку  (образ первого преобразования) т.е.
(образ первого преобразования) т.е.  , затем – второе преобразование
, затем – второе преобразование  , переводящее точку
, переводящее точку  (прообраз второго преобразования) в точку
(прообраз второго преобразования) в точку  (образ второго преобразования), т.е.
(образ второго преобразования), т.е. 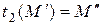 .
.
Результирующее (сквозное) преобразование  , переводящее
, переводящее  в
в  и есть произведение (умножение, композиция) преобразований, т.е.
и есть произведение (умножение, композиция) преобразований, т.е.  . Оно записывается и так:
. Оно записывается и так:  (преобразование, выполняемое первым, пишут в произведении справа). Более подробно запишем:
(преобразование, выполняемое первым, пишут в произведении справа). Более подробно запишем:
 .
.
Рассмотрим несколько примеров преобразования плоскости, известных всем из элементарной геометрии [8].
Пример 1. Пусть на плоскости дана прямоугольная система координат (рисунок 1.10) и точка  с координатами
с координатами  и
и 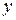 , т.е.
, т.е. 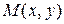 . Выполним параллельный перенос, или трансляцию плоскости(преобразование
. Выполним параллельный перенос, или трансляцию плоскости(преобразование  ) на вектор
) на вектор  , который переводит всякую точку
, который переводит всякую точку  плоскости в точку
плоскости в точку 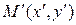 . Таким образом,
. Таким образом, 
 , где
, где  .
.
Уравнение данного преобразования  имеет вид:
имеет вид:
 (1.1)
(1.1)
Будем пользоваться и такой записью:
 . (1.2)
. (1.2)
 |
Рисунок 1.10 – Трансляция, или параллельный перенос
плоскости на вектор 
При 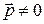 трансляция не имеет неподвижных точек. Трансляция переводит всякую прямую линию в параллельную ей прямую.
трансляция не имеет неподвижных точек. Трансляция переводит всякую прямую линию в параллельную ей прямую.
Пример 2. Пусть  ,
,  – соответственно трансляции на векторы
– соответственно трансляции на векторы 
 ,
, 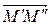
 , т.е.
, т.е.  ,
,  (рисунок 1.11). Тогда
(рисунок 1.11). Тогда  будет трансляцией на вектор
будет трансляцией на вектор 
 , т.е.
, т.е. 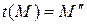 .
.
 |
Рисунок 1.11 – Композиция трансляций 
Оказывается, последовательность выполнения трансляций не влияет на окончательный результат (рисунок 1.12), что можно проверить аналитически.
Таким образом,  . Такие преобразования называются перестановочными, или коммутативными.
. Такие преобразования называются перестановочными, или коммутативными.
 |
Рисунок 1.12 – Композиция трансляций 
Пример 3. Преобразование  , переводящее каждую точку
, переводящее каждую точку  плоскости в точку
плоскости в точку 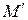 , симметричную ей относительно фиксированной прямой
, симметричную ей относительно фиксированной прямой  является симметрией относительно этой прямой, которая называется осью симметрии. В частном случае, когда осью симметрии служит одна из координатных осей, например
является симметрией относительно этой прямой, которая называется осью симметрии. В частном случае, когда осью симметрии служит одна из координатных осей, например  (рисунок 1.13), закон преобразования будет иметь вид:
(рисунок 1.13), закон преобразования будет иметь вид:
 (1.3)
(1.3)
или
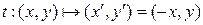 . (1.4)
. (1.4)
Неподвижными точками осевой симметрии являются только те точки, которые принадлежат оси симметрии, неподвижными прямыми являются ось симметрии и любая прямая ей инцидентная (принадлежащая).

Рисунок 1.13 – Осевая симметрия
Пример 4. Найти произведение преобразований  и
и 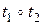 , где
, где  и
и  соответственно осевая симметрия (1.4) и трансляция (1.2).
соответственно осевая симметрия (1.4) и трансляция (1.2).
Для первого случая имеем:
 ,
,
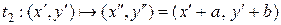 ,
,
 .
.
Аналогично для второго случая:
 ,
,
 ,
,
 .
.
Данный пример показывает, что осевая симметрия и трансляция не коммутируют (произведения  и
и 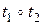 различны). Поэтому в общем случае умножение преобразований не коммутативно.
различны). Поэтому в общем случае умножение преобразований не коммутативно.
Кроме коммутативности следует отметить, что умножение преобразований обладает свойством ассоциативности:
 .
.
Преобразование  обладает следующим свойством:
обладает следующим свойством:
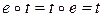 .
.
При рассмотрении обратного преобразования следует отметить, что
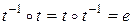 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 703; Нарушение авторских прав?; Мы поможем в написании вашей работы!