Группы и виды преобразований

1.3.1 Общие положения

Множество преобразований 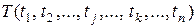составляют группу, если:

1) произведения 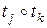всех пар преобразований из 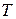принадлежат ;

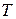2) для каждого преобразования 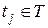есть обратное преобразование .

Множество преобразований 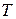, обладающее первым свойством, называется замкнутым относительно операции умножения. Если оно обладает вторым свойством, то называется замкнутым относительно операции обращения, то есть перехода к обратному преобразованию. Поэтому можно дать и другое определение группы преобразований: группа преобразований – это такое множество, которое замкнуто относительно операций умножения и обращения.

Далее важными свойствами группы преобразований являются следующее:

3) группа содержит тождественное преобразование , это можно отметить как ;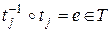

4) произведение преобразований подчиняется ассоциативному закону (см. п.1.2.3, пример 4):

.

Подкрепим понятие группы преобразований примером 2 (п. 1.2.3).

Пусть имеем множество 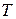параллельных переносов на плоскости, заданных своими векторами. Это множество составляет группу, так как:

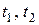1) произведением двух переносов соответственно на вектор и 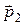также является переносом на вектор (см. рисунки 1.11 и 1.12), т. е. ;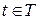

2) для любого переноса 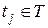есть обратное преобразование 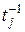, задаваемое обратным вектором;

3) множество 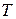содержит тождественное преобразование , т.е. – перенос на нулевой вектор;

4) подчинение преобразований ассоциативности рассмотрено выше:

.

1.3.2 Основные группы преобразований

Наиболее обширную группу составляют так называемые топологические преобразования. Основным инвариантом этих преобразований являются взаимная однозначность (этим условием должны обладать, как указано выше, все преобразования) и непрерывность.

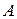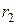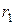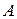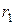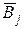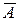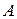Преобразование называется непрерывным в точке , если выполняется следующее условие: для всякого положительного числа можно найти такое положительное число , что каждая точка , отстоящая от точки на расстояние меньшее, чем , отображается в точку , отстоящую от образа точки на расстояние меньше, чем 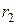(рисунок 1.14).

Рисунок 1.14 – Интерпретация условия непрерывности [5]

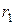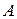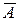Иными словами, круг радиуса с центром в точке , где , преобразуется в некоторую фигуру , которая полностью находится внутри окружности с центром в точке и радиусом, равным 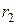. Соответственные фигуры называются топологически эквивалентными, или гомеоморфными.

Свойства гомеоморфных фигур, т.е. свойства фигур, инвариантных относительно топологических преобразований, изучает топология – геометрия, характеризующаяся необычайной широтой класса геометрических объектов. Это объясняется тем, что понятие гомеоморфизма не требует для своего определения никаких классических понятий типа расстояния, прямолинейности и т. д. В топологии изучаются наиболее общие свойства топологических фигур.

Внутри группы топологических преобразований есть подмножества других более частных преобразований, также составляющих группы. Такие группы преобразований называются подгруппами топологических преобразований. Естественно, что в состав инвариантов подгруппы входят инварианты «охватывающей» группы преобразований. Но подгруппа преобразований имеет и свои дополнительные инварианты, выделяющие ее их группы.

В сою очередь, подгруппа может содержать другую подгруппу. Поэтому группа топологических преобразований состоит из «вложенных друг в друга» подгрупп. Таких подгрупп достаточно много. Обычно среди них выделяют основные группы (подгруппы), которые представлены на рисунке 1.15.

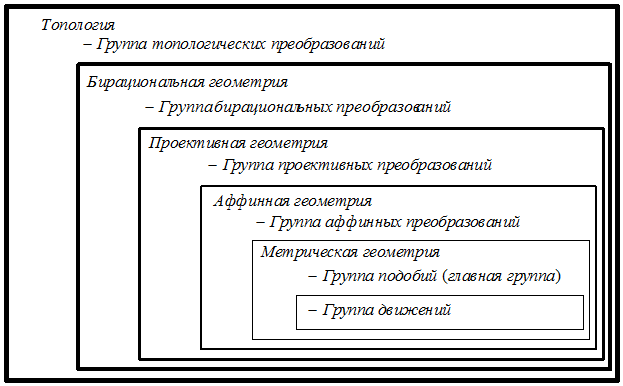Рисунок 1.15 – Основные группы (подгруппы) преобразований

Дадим краткий обзор этих подгрупп преобразований.

Бирациональные преобразования плоскости в декартовых координатах дробно-рациональными функциями:

,

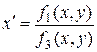(1.5)

,

где 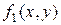, , 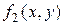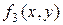– алгебраические многочлены п -го порядка. При 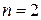преобразования называются квадратичными, при – кубическими.

Свойства фигур, инвариантных относительно бирациональных преобразований (их еще называют кремоновы преобразования), изучает бирациональная геометрия, являющаяся важным разделом алгебраической геометрии.

Предметом бирациональной геометрии являются всевозможные алгебраические многообразия (кривые линии, поверхности и т. д.).

Бирациональные преобразования нашли широкое применение в прикладной геометрии. Они используются для конструирования кривых линий и поверхностей с целью аппроксимации технических кривых и поверхностей их дугами и отсеками, обводами из их дуг и отсеков, а также моделирования всевозможных процессов и зависимостей [9, 10].

Проективные преобразования составляют группу бирациональных (порядок преобразования 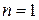). Они задаются в декартовых координатах дробно-линейными функциями. Эти функции имеют вид (1.5), где 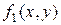, , 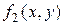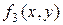– многочлены первой степени.

Основным инвариантом этих преобразований является порядок, т.е. в проективных преобразованиях в отличие от бирациональных порядки образа и прообраза равны: прямая преобразуется в прямую, кривая п -го порядка – в кривую п -го порядка.

Свойства фигур проективного пространства, сохраняющиеся при выполнении проективных преобразований, изучает проективная геометрия [5, 7, 11,. Методы проективной геометрии широко применяются при решении прикладных задач. Например, теория перспективных изображений, реконструкции архитектурных сооружений по их изображениям, фотоснимкам и т. д.

Подгруппу проективных преобразований составляют аффинные преобразования. Свойства фигур, инвариантные относительно аффинных преобразований, изучает аффинная геометрия. Предмет аффинной геометрии составляют фигуры аффинного пространства, их свойства и отношения (принадлежность, пересечение, параллельность и т. д.).

В метрической (элементарной) геометрии фигуры считаются равными (конгруэнтными), если они могут быть совмещены движением. Длины отрезков, площади фигур, углы и отношения длин отрезков являются инвариантами группы движений. В то же время, углы и отношения длин отрезков остаются инвариантами не только при движениях, но и при преобразованиях подобия (т.е. при преобразованиях главной группы). Поэтому элементарную геометрию, предметом которой являются фигуры пространства с евклидовой метрикой, их свойства и отношения (принадлежность, пересечение, параллельность, перпендикулярность и т. д.), можно рассматривать как теорию инвариантов группы движений и главной группы. Рассмотрим подробнее эти группы.

Группа движений. Движением называется такое преобразование плоскости, которое сохраняет расстояние между точками:

.

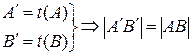Рассмотрим простейшие свойства движений (см. п. 1.2.3):

1) движения плоскости образуют группу: из определения ясно, что произведение двух движений есть движение (пример 2, п. 1.2.3).

2) движение сохраняет прямолинейное расположение точек:

– пусть 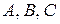– три точки плоскости, лежащие на прямой плоскости, где точка 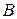лежит между точкам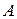и и ;

– точки – их образы при движении , тогда

,

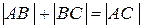однако,

, , ,

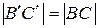следовательно,

,

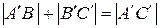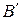поэтому точки лежат на одной прямой, причем точка лежит между точками и ;

3) движение сохраняет порядок точек на прямой, т.е. сохраняет отношение «между», что доказано в предыдущем пункте.

Из свойств 2 и 3 следует, что:

4) движение переводит прямую в прямую, отрезок – в равный ему отрезок, полупрямую – в полупрямую, треугольник – в равный ему треугольник, угол – в равный ему по величине угол, параллельные прямые – в параллельные прямые.

Движения (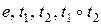), которые не содержат в качестве сомножителя осевую симметрию характерны тем, что сохраняют ориентацию плоскости. Они называются движениями 1-го рода.

Движения (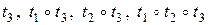), содержащие в качестве сомножителя осевую симметрию , меняют ориентацию плоскости на обратную. Они называются движениями 2-го рода.

Движения 1-го рода образуют группу (подгруппу группы движений). Действительно, если два движения сохраняют ориентацию плоскости, то их произведение, а также обратное к каждому, есть также движение, сохраняющее ориентацию плоскости.

Другими подгруппами группы движений (и группы движений 1-го рода) является группа трансляций и группа вращений вокруг фиксированной точки.

Движения 2-го рода не образуют группы, так как произведение двух движений 2-го рода есть движение 1-го рода.

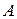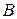Группа подобий (главная группа). Преобразование плоскости называется подобием с коэффициентом , если для любых двух точек и плоскости имеем:

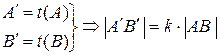. (1.6)

Дата добавления: 2014-12-27