
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
СМО смешанного типа с различными характеристиками каналов
|
|
|
|
Smo2.m
% Двухканальная СМО с ожиданием и отказами
% Время ожидания обслуживания ограничено
% Продвижение времени по особым состояниям
function smo2
t=0; % начальный момент времени
X=0; % состояние системы в начальный момент времени
tm=100; % конечный момент времени
s0=0;s1=0;s2=0;s3=0;s4=0; % время пребывания в состоянии
n=0; % число заявок, поступивших в систему
k=0; % число обслуженных заявок
w=0; % число заявок, не дождавшихся обслуживания
vsol=[];
disp('Время перехода Состояние');
while t<tm
sol=[t,X];
if X==0
q=exprnd(20);
s0=s0+q;
n=n+1;
t=t+q;
X=1:
else
if X==1
q=exprnd(20);
p=exprnd(40);
dt=min(p,q);
s1=s1+dt;
t=t+dt;
if p<=q
k=k+1;
X=0;
elseif p>q
n=n+1;
X=2;
end
else
if X==2
q=exprnd(20);
p=exprnd(20);
dt=min(p,q);
s2=s2+dt;
t=t+dt;
if p<=q
k=k+1;
X=1;
elseif p>q
n=n+1;
X=3;
end
else
if X==3
q=exprnd(20);
p=exprnd(20);
p1=exprnd(30);
dt=min(p,q);
s3=s3+dt;
t=t+dt;
if p>q
n=n+1;
X=4;
elseif p1<=dt
w=w+1;
X=2;
elseif p1>dt & p<=q
k=k+1;
X=2;
end
else
if X==4
q=exprnd(20);
p=exprnd(20);
p1=exprnd(15);
dt=min(p,q);
s4=s4+dt;
t=t+dt;
if p1<=dt
w=w+1;
X=3;
elseif p<=q
k=k+1;
X=3;
end
end
end
end
end
end
disp(sol)
vsol=[vsol,sol];
if t>tm
tl=t-q;
end
end
pp=s1/tl;
sprintf('Вероятность, что система находится в состоянии один канал занят, в очереди нет заявок= %g',pp)
Программа для описания функционирования системы без учета ограничений на время ожидания обслуживания легко получается из данной, если убрать дополнительные условия, поэтому не будем приводить ее текст.
В большинстве задач моделирования СМО в исходной постановке процесс функционирования не может рассматриваться как марковский процесс, если в качестве состояния принимать количество заявок в системе. К таким системам можно отнести многофазные СМО, СМО с потоками событий, отличающимися от простейших, многоканальные СМО с различными характеристиками каналов и др. Однако во многих случаях процессы в этих системах можно свести к марковским, используя прием расширения пространства состояний.
Рассмотрим далее в качестве примера СМО с двумя каналами обслуживания и одним местом в очереди. Каждый канал имеет свои характеристики – интенсивности обслуживания 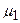 и
и 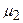 ,
,  – интенсивность потока заявок.
– интенсивность потока заявок.
Очевидно, что количество заявок в системе как состояние не описывается марковским процессом, т.к. очередное состояние (т.е. количество заявок) не определяется только количеством заявок в системе на предыдущем шаге, а зависит также и от того, какой именно из каналов мог быть занят (или освобожден) на предыдущем шаге.
Процесс может быть сведен к марковскому, если характеристику канала ввести в состояние. Например, для данной задачи ввести следующие состояния:
St0_0_0 – заявок в системе нет;
St1_0_0 – в системе одна заявка, занят канал с интенсивностью освобождения 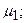
St0_1_0 –в системе одна заявка, занят канал с интенсивностью освобождения 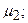
St1_1_0 – в системе две заявки, заняты оба канала;
St1_1_1 – в системе три заявки, оба канала и место в очереди заняты.
Поскольку каналы неравноценны, следует ввести правила занятия каналов:
1. При наличии очереди занимается освободившийся канал.
2. При занятом одном канале занимается свободный канал.
3. При отсутствии заявок в системе при появлении заявки занимается либо:
а) Какой-то определенный канал, например, канал K1 (или K2);
б) Занимается канал, освободившийся раньше;
в) Занимается канал, время функционирования которого меньше.
Граф переходов можно представить в виде, изображенном на рисунке 5.20
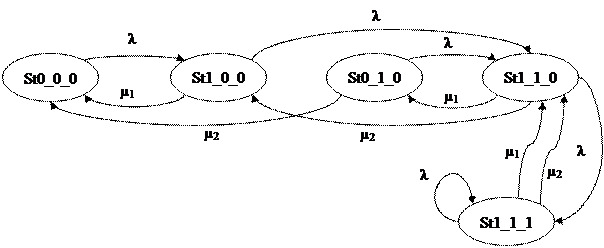
Рис. 5.20 Граф переходов для СМО смешанного типа с различными
характеристиками каналов
SF-диаграмма представлена на рисунке 5.21
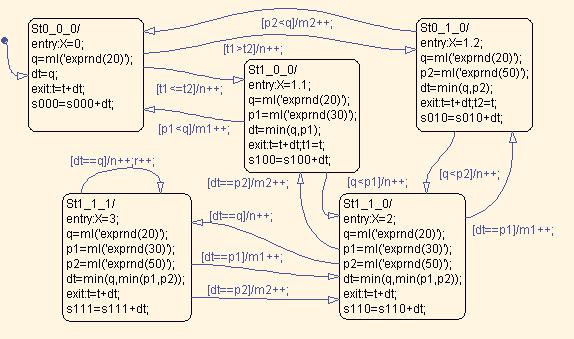
Рис. 5.21 СМО смешанного типа с различными характеристиками каналов
Примем правило занятия свободных каналов в соответствии с пунктом 3.б.
SIMULINK-схема приведена на рисунке 5.22. Здесь X – код состояния, m1 – число заявок, обработанных первым каналом, m2 – число заявок, обработанных вторым каналом, r – число заявок, получивших отказ, n – число заявок, t – время перехода, S000,S100,S010,S110,S111 – время пребывания в соответствующем состоянии, t1,t2 – время освобождения первого и второго каналов соответственно.
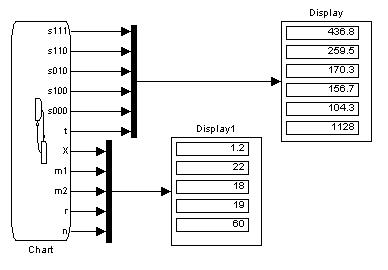
Рис. 5.22 Simulink-схема для СМО смешанного типа
Настройки данной системы выглядят следующим образом (рис. 5.23):
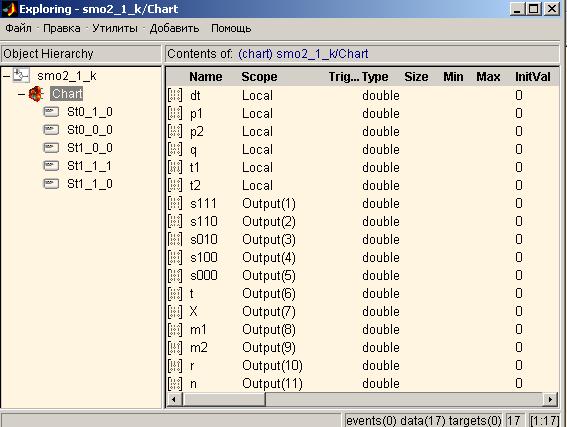
Рис. 5.23 Настройки системы
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 731; Нарушение авторских прав?; Мы поможем в написании вашей работы!