Общие положения теории планирования эксперимента

В ТПЭ исследуемый объект (реальный объект, модель объекта) рассматривается как "черный ящик", имеющий входы v (управляемые независимые параметры, или внутренние параметры) и выходы y [3, 6].По традиции входные управляемые переменные (внутренние параметры) обозначим: v = x1, x2,..., хn.

Переменные v принято называть факторами. Теория ПЭ изучает только активный тип экспериментов, когда имеется возможность независимо и целенаправленно менять значения факторов v во всем требуемом диапазоне. Факторы в эксперименте бывают качественными и количественными. Качественные факторы можно квантифицировать или приписать им числовые обозначения, тем самым перейти к количественным значениям. В дальнейшем будем считать, что все факторы являются количественными и представлены непрерывными величинами (если другое не оговорено особо). Переменным v можно сопоставить геометрическое понятие факторного пространства – пространства, координатные оси которого соответствуют значениям факторов. Совокупность конкретных значений всех факторов образует точку в многомерном факторном пространстве. Примерами факторов являются: интенсивность потока запросов к базе данных, скорость передачи данных по каналу, объем запоминающего устройств. Кроме того, на объект воздействуют возмущающие факторы, они являются случайными и не поддаются управлению.

Область планирования задается интервалами возможного изменения факторов x_i,min < x_i < x_i,max для i =1, 2, …, n, где n =k – количество факторов. В теории ПЭ часто используют нормализацию факторов, т.е. преобразование натуральных значений факторов в безразмерные (нормированные) величины. Переход к безразмерным значениям x_i задается преобразованием

Х i = (хi – хi 0)/D хi,

(1.1)

где х_i – натуральное (реальное) значение фактора, х_iб = х_{i 0} – базовое значение основного уровня фактора, соответствующее нулю в безразмерной шкале, Δ х_i – интервал (шаг) варьирования фактора х_i.

Выходные параметры объекта проектирования у1, у2,..., уm называются переменными состояния, или функцией отклика. Различают экономические и технологические переменные состояния.

В качестве экономических используют производительность, себестоимость и другие показа­тели. Технологическими переменными служат качество продукта, выход целевого продукта, надежность получаемых изделий и др. Объект исследования может иметь несколько переменных состоя­ния, их количество следует сократить до минимума.

Опыт показывает, что в большинстве случаев удается огра­ничиться одной переменной состояния, и тогда вектор У превраща­ется в скалярную величину у.

Если переменных состояния несколько, то эксперимент прово­дится по каждой из них, а затем решается компромиссная задача.

При выборе переменной состояния необходимо учитывать сле­дующие требования:

1) переменная состояния должна иметь количественную харак­теристику, т. е. измеряться;

2) переменная состояния должна однозначно измерять эффек­тивность объекта исследования; это требование эквивалентно кор­ректной постановке задачи;

3) переменная состояния должна быть статистически эффектив­ной, т. е. обладать возможно меньшей дисперсией при проведении опытов; это позволяет хорошо различать опыты.

Правильный выбор переменной состояния объекта исследова­ния повышает шансы экспериментатора на успех.

При выборе факторов нужно выполнять сле­дующие требования:

1) фактор должен быть регулируемым, т. е. с помощью опреде­ленного регулирующего устройства фактор можно изменять от зна­чения x1 до значения x2 (системотехники называют это операционной определенностью).

2) точность измерения и управления факторов должна быть из­вестна и достаточно высока (хотя бы на порядок выше точности из­мерения выходной переменной); очевидно, что низкая точность из­мерения факторов уменьшает возможности воспроизведения экспери­мента.

К факторам и переменным состояния одновременно также предъ­является ряд требований:

1) факторы и переменные состояния должны иметь области опре­деления, заданные технологическими или принципиальными огра­ничениями; области определения факторов должны быть таковы, чтобы при различных их комбинациях переменные состояния не выходили за свои ограничения;

2) между факторами и переменными состояниями должно существовать однозначное соответствие; оно позволит в основном эксперименте построить математическую модель объекта исследования и решить поставленную задачу эксперимента.

Метод наименьших квадратов позволяет получить описание объекта по любым данным, лишь бы матрица системы нормальных уравнений была невырожденной. Поэтому с появлением ЭВМ возникла идея — получать математические описания технологических процессов, пользуясь в качестве исходных данных результатами нормальной эксплуатации процесса.

В реальных условиях технологический процесс все время испытывает случайные колебания режима. Сегодня значения контроли­руемых факторов несколько иные, чем вчера, а завтра будут еще немного другими. Нельзя ли каждое изменение режима рассматри­вать как эксперимент, и, обработав совокупность таких «экспери­ментов» методом наименьших квадратов, получить описание про­цесса, а затем использовать это описание для управления и опти­мизации? Такой подход получил название пассивного экспе­римента.

Достоинство пассивного эксперимента—отсутствие затрат на опыты: данные получаются «сами собой». Но надежды, возлагав­шиеся на этот метод, в большинстве случаев не оправдались.

Анализ неудач пассивного эксперимента выявил несколь­ко их причин.

Во-первых, в нормальных условиях колебания режи­ма малы, опытные точки находятся близко одна к другой. Хорошо известно, что чем ближе опытные точки, тем сильнее влияют на описание случайные ошибки. Действительно, различия в получае­мых значениях отклика при этом малы, и эти малые различия пло­хо выделяются на фоне шума — случайных ошибок. Поэтому зна­чения коэффициентов регрессии оцениваются со значительными ошибками.

Во-вторых, в пассивном эксперименте факторы сильно коррелированны. Это делает крайне ненадежным ана­лиз влияния отдельных факторов—всегда может оказаться, что влияет не данный фактор, а другой, с ним коррелированный.

В-третьих, сами значения факторов в производственных усло­виях часто измеряются с заметными ошибками; поэтому применение метода наименьших квад­ратов в его обычном варианте становится некорректным.

В связи с этим в теории экспери­мента любой эксперимент, при планировании которого не учтено влияние плана эксперимента на статистические свойства получае­мых оценок, часто называют пассивным. Ему противопоставляют активный эксперимент, в основе которого лежит планирование эксперимента (то есть управление условиями его проведения)

Наи­более широко в настоящее время используются планы так называемого экстремально­го эксперимента, разработанные для определения оптимальных условий протекания процессов в объектах исследования.

Оптимум определяется по математической модели объекта исследования, которую ищут в виде полиномиального уравнения (уравнения регрессии).

Логи­ку появления полинома как математической модели объекта ис­следования можно объяснить следующим образом. Исследователь полагает, что математическую модель объекта прин­ципиально можно представить дифферен-циальными уравнениями. В общем виде искомое решение можно пред­ставить функцией:

y= F (X,b), (1.2)

где у— переменная состояния объекта исследования; Х— матри­ца факторов; b — матрица коэффициентов.

Коэффициенты b полинома можно интерпретировать как коэф­фициенты ряда Тейлора, в который «удается» разложить решение в окрестностях некоторой точки.

Пользуясь статистическими методами и учитывая конечность экспериментальных данных, можно получить оценки коэффи­циентов регрессии b в уравнении (1).

Уравнение (1) называют уравнением регрессии и широко используют для получения математиче­ской модели объекта исследования.

Прежде чем приступить к планированию эксперимента, необходимо убедиться в том, что опыты воспроизводимы, Для этой цели проводят N серий из k параллельных опытов в рассматриваемой области изменения влияющих факторов.

Результаты опытов заносятся в таблицу:

Таблица 1.1

Номер серии опытов	Результаты параллельных опытов	yj,средн.
	Y11	Y12	………..	Y1k	Y1средн
	Y21	Y22	………..	Y2k	Y2средн
	Y31	Y32	………..	Y3k	Y3средн
j	Yj1	Yj2	………..	Yjk	Yjсредн
N	YN1	YN2		YNk	YNсредн.

Определяется среднее арифметическое значение функции отклика для любой серии опытов j (j=1,…,N):

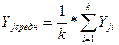
Оценивается дисперсия для каждой серии параллельных опытов:

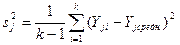
Определяется расчётное значение критерия Кохрена: .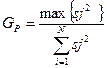

По специальным таблицам определяют табличное значение Кохрена - G_T. Они зависят от доверительной вероятности P(как правило P=0.95),от N и от f=k-1.

Если выполняется условие G_p 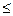G_T, то опыты считаются воспроизводимым

Определяется погрешность эксперимента. Оценка дисперсии воспроизводимости рассчитывается по формуле:

,

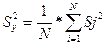с ней связано число степеней свободы N*(k-1)

В последовательно­сти реализации планов можно выделить следующие этапы:

1) оценка априорной информации и отсеивание факторов, не­существенных для конкретного объекта исследования;

2) получение математической модели объекта в виде линейной функции отклика;

3) поиск оптимальной области объекта по линейной функции отклика;

4) получение математической модели объекта исследования об­ласти оптимума в виде нелинейной функции отклика;

5) поиск оптимальной координаты факторного пространства в области оптимума.

Экстремальный эксперимент заканчивается определением оптимальной коорди­наты, соответствующей оптимальным условиям протекания процес­сов объекта исследования.

В подавляющем большинстве РЭС и технологические процессы их изготовления являются сложными, на процесс влияет не один, а ряд факторов.

Возможны два подхода к исследованию таких многофакторных систем. Первый можно описать формулой: «Изменяй факторы по одному». Исследование системы разбивается на серии, в пределах каждой из которых изменяется (варьируется) лишь один фактор, а остальные неизменны. В следующей серии изменяется второй фак­тор и т. д. Идея другого подхода— построить план экспери­мента, предусматривающий изменение всех влияющих факторов, с тем, чтобы этот план обеспечивал максимум точности, минимум корреляции и другие хорошие статистические свойства. Такой экс­перимент называют многофакторным.

Долгое время в науке господствовал первый подход. Его глав­ное преимущество—наглядность: данные каждой серии легко поддаются интерпретации.

Один из важных результатов теории планирования эксперимен­та заключается в том, что второй подход—значительно эф­фективнее первого. При том же объеме эксперимента и той же точности опытов получается большая точность резуль­татов.

Геометрическим образом совокупности независимых перемен­ных х и зависимой переменной у является пространство n+1 изме­рения, где n — число независимых переменных; (n+1)-е измерение относится к у. В этом пространстве зависимости у от всех х соот­ветствует n-мерная поверхность, которую обычно называют по­верхностью отклика (результат опыта рассматривается как отклик системы на опыт—заданную совокупность независи­мых переменных, или входов).

План эксперимента указывает расположение опытных точек в n-мерном пространстве независимых переменных (факторном пространстве), или иными словами, условия всех опытов, которые следует провести. Чаще всего план эксперимента задается в виде матрицы планирования — прямоугольной таблицы, каждая строка которой отвечает условиям определенного опыта, а каждый столбец — значениям какой-то из независимых перемен­ных в разных опытах.

Полным факторным экспериментом называется система опытов, содержащая все возможные неповторяющиеся комбинации уровней варьирования факторов.Для удобства вычислений коэффициентов регрессии все фак­торы в ходе полного факторного эксперимента варьируют на двух уровнях: нижнем -1 и верхнем +1, соответствующих значениям нормированных переменных X1,X2,……Xn.Таким образом, полным факторным экспериментом называется система опытов, содержащая все возможные неповторяющиеся комбинации уровней варьирования факторов.

В табл. 1.2 приведены условия опытов полного трехфакторного эксперимента. Эти опыты соответствуют в факторном простран­стве вершинам куба с центром в начале координат.

Таблица 1.2

Номер опыта	Факторы	Функция отклика
X1	X2	X3
	-1	-1	-1	y1
	+1	-1	-1	у2
	-1	+1	-1	у3
	+1	+1	-1	у4
	-1	-1	+1	у5
	+1	-1	+1	у6
	-1	+1	+1	у7
	+1	+1	+1	у8

Каждый фактор принимает лишь два значения — варьи­руется на двух уровнях, верхнем и нижнем. Поэтому общее число экспериментов N=2 ⁿ.

Пример. В четырех опытах исследуется влияние 3 факторов:температуры T,К, давления р, МПа, и времени t, с, на выход продукта.

Здесь в любом из опы­тов температура—либо 1000 К (нижний уровень), либо 1200 К (верхний уровень); аналогично варьируются р и t.

Таблица 1.3

	Температура	Давление	Время
Основной уровень
Интервал варьирования
Верхний уровень
Нижний уровень

Матрица планирования эксперимента для этого случая может иметь вид:

Таблица 1.4

№№	T	P	t

Из таблицы видны основные принципы построения матриц планирования полного факторного эксперимента:

Матрица планирования ПФЭ обладает следующими свойствами:

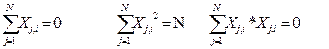
где j- номер опыта; i— номер фактора,(l¹m) Свойство, выраженное последним уравнением, называется ортогональностью матрицы.

Оно позволяет вычислять коэф­фициенты регрессии по простым формулам независимо друг от друга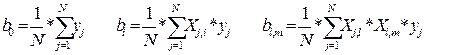

Расширенная матрица—это матрица, дополненная столб­цами, учитывающими взаимодействия факторов. На прак­тике, как правило, ограничиваются парными взаимодейст­виями.

Коэффициенты регрессии рассчитываются методом наи­меньших квадратов. Основное условие метода формулируется следующим образом: коэффициенты регрессии определяются на основании минимизации суммы квадратов отклонений между экспериментальными уэ, и рассчитанными по уравне­нию регрессии yр значениями функции отклика:

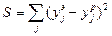
После определения коэффициентов регрессии определяем значимость этих коэффициентов. Все коэффициенты подразделяются на значимые и незначимые. Для определения значимости коэффициентов регрессии сравнивается погрешность вычисления коэффициента с погрешностью экспериментальных данных - 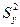. Вычисляется доверительный интервал:

.

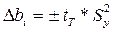Здесь t_T - табличное значение критерия Стьюдента, которое находится по числу степеней свободы и доверительной вероятности. Тогда значимость оценивают, сравнивая абсолютные значения коэффициента и доверительного интервала.

.Незначимые коэффициенты отбрасываются из уравнения регрессии, после чего записывается окончательный вид уравнения регрессии. Это уравнение проверяется на адекватность. Для этого вычисляется оценка дисперсии адекватности:

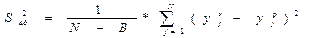
Здесь B- число значимых коэффициентов регрессии.

Вычисляют расчётное значение критерия Фишера: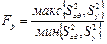

По таблице находят табличное значение критерия Фишера. Оно зависит от доверительной вероятности P, числа степеней свободы f_ад= N-B и f= N*(k-1). На основании этого делается вывод об адекватности или неадекватности уравнения регрессии. Уравнение регрессии считается адекватным, если выполняется условие: F_р 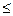F_T.

Чем меньше B, тем больше N-B—в этом одна из главных целей, достигаемых при исключении незначимых членов.

Если уравнение неадекватно, переходят к более сложной модели (например, повышают степень многочлена), для чего обычно тре­буется постановка добавочных опытов. Иногда можно обойтись без дополнительного эксперимента, если соответствующим образом преобразовать переменные у или х.

Совокупность основных уровней всех факторов представляет собой точку в пространстве параметров, называемую центральной точкой плана или центром эксперимента. С геометрической точки зрения нормализация факторов равноценна линейному преобразованию пространства факторов, при котором проводятся две операции: перенос начала координат в точку, соответствующую значениям основных уровней факторов; сжатие – растяжение пространства в направлении координатных осей.

Активный эксперимент включает: систему воздействий, при которых воспроизводится функционирование объекта; регистрацию отклика объекта. План эксперимента задает совокупность данных, определяющих количество, условия и порядок реализации опытов. Опыт составляет элементарную часть эксперимента и предусматривает воспроизведение исследуемого явления в конкретных условиях с последующей регистрацией результата. В условиях случайности в одних и тех же условиях проводятся параллельные (повторные) опыты в интересах получения статистически устойчивых результатов. Опыт u предполагает задание конкретных значений факторам v _u = v _{1 u} , v _{2 u} , …, v_ku, а совокупность значений факторов во всех N точках плана эксперимента образует матрицу плана

v 11, v 21, …, vk 1 v 12, v 22, …, vk 2 ..... v 1 N , v 2 N , …, vkN.

(1.2)

Строки матрицы соответствуют опытам, столбцы – факторам, элемент матрицы v_iz задает значение z- го фактора в i- м опыте.

Вектор y называется откликом. В ТПЭ обычно изучается ситуация, в которой вектор отклика y состоит из одного элемента y. При наличии нескольких составляющих вектора y, каждую из них можно исследовать отдельно. Зависимость отклика от факторов носит название функции отклика, а геометрическое представление функции отклика – поверхности отклика. Функция отклика рассматривается как показатель качества или эффективности объекта. Этот показатель является функцией от параметров – факторов. На практике широкое распространение получили простые функции вида М{ y^' } = bf (v), где b= (b ₀, b ₁, …, b_h ) – вектор неизвестных параметров модели размерности h +1, f (v)=(f ₀(v), f ₁(v), …, f_h (v)) – вектор заданных базисных функций, М{ y^' } – математическое ожидание функции отклика. Такое представление функции отклика соответствует линейной по параметрам модели регрессионного анализа, т.е. функция отклика есть линейная комбинация базисных функций от факторов.

Вследствие влияния на результаты экспериментов случайных воздействий истинные значения коэффициентов можно определить только приближенно. Оценку b = (b₀, b₁, …, b _h) вектора неизвестных параметров b находят по результатам экспериментов, в ходе которых получают значения y_u при заданных значениях факторов v _u. Эти оценки обычно рассчитываются с помощью метода наименьших квадратов (МНК) на основе выборок значений факторов и откликов системы на воздействия [8]. В качестве оценки b вектора b выбирается такое значение, которое минимизирует

,

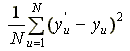где y^'_u – вычисленное на модели значение функции отклика в u -й точке факторного пространства. Приравнивая нулю частные производные от данной квадратичной формы, взятые по переменным b₀, b₁, …, b _h, можно получить систему уравнений вида

,

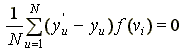где i = 0, 1, 2, …, h. Значение b находят путем решения этой системы уравнений. Решение системы возможно при линейной независимости базисных функций.

Если не принимать специальных мер, то оценки коэффициентов b станут взаимозависимыми, и полученное выражение для функции отклика можно рассматривать только как интерполяционную формулу, что затрудняет ее физическую интерпретацию и последующие расчеты. Однако, формируя специальным образом матрицу плана, можно получить независимые значения b. И эти величины будут характеризовать вклад каждого фактора в значение функции отклика.

Итак, задача заключается в определении общей формы записи функции отклика y^'. В большинстве случаев вид этой функции, получаемый из теоретических соображений, является сложным для практического применения, а при неполном знании объекта вообще неизвестен. По данным причинам функцию целесообразно представить в универсальном, удобном для практического применения виде, чему соответствует представление в виде полинома. Тогда системой базисных функций является совокупность степенных функций с целыми неотрицательными значениями показателей степени. Полиномиальная форма представления функции отклика примет вид

y^' = b0 + b1 x 1 + …+ b kxk + b12 x 1 x 2 + b13 x 1 x 3+… +b k –1, k xk –1 xk + +b11 x ^21 + …+b kkx ^2 k + … + e,

(1.3)

где e – случайная величина, характеризующая ошибку опыта.

Такая функция отклика линейна относительно неизвестных коэффициентов и будет полностью определена, если заданы степень полинома и коэффициенты.

Степень полинома обычно задается исследователем априорно и уточняется в ходе исследования. На практике наибольшее распространение получили полиномы первого и второго порядка, соответственно линейные и квадратичные модели. Коэффициенты полинома принято называть эффектами факторов.

Иногда функцию отклика целесообразно представить в другом виде, например, в виде степенной функции, так как достижение заданной точности требует применения полинома высокого порядка. Однако использование функций, нелинейных относительно неизвестных параметров, усложняет вычисления, затрудняет оценку их свойств.

В некоторых случаях задачу можно упростить путем искусственного преобразования нелинейной функции в линейную. При этом требуется соответствующее преобразование и результатов экспериментов.

Применение ТПЭ основано на ряде допущений, а именно [2, 6]: функция отклика содержит в своем составе неслучайную и случайную составляющую. Многие показатели качества автоматизированных систем обработки информации носят случайный характер. Это требует многократного повторения опытов в одних и тех же условиях в целях получения статистически устойчивых результатов, а получаемые оценки показателей должны обладать свойствами состоятельности, эффективности, несмещенности и достаточности. Оценки типовых показателей формируются путем усреднения результатов наблюдений. Поэтому при достаточно большом количестве наблюдений можно считать, что случайная составляющая e распределена по нормальному закону с нулевым математическим ожиданием, что позволяет получить несмещенную оценку математического ожидания функции отклика в конкретной точке плана. Будем также считать, что величина e имеет дисперсию, не зависящую от значений факторов. Иначе говоря, результаты, полученные путем усреднения повторных опытов в каждой точке плана, представляют собой независимые, нормально распределенные случайные величины;

факторы v ₁, v ₂, …, v_k измеряются с пренебрежимо малой ошибкой по сравнению с ошибкой в определении величины y (учет помех в задании факторов приводит к трудно разрешимым проблемам в оценке коэффициентов функции отклика). Ошибка в определении значения функции отклика объясняется не столько погрешностью измерений, сколько влиянием на результат работы системы неучтенных или случайных факторов, например различиями в формируемой последовательности случайных чисел при статистическом моделировании;

дисперсии среднего значения функции отклика в различных точках равны друг другу (выборочные оценки дисперсии однородны). Это означает, что при многократных повторных наблюдениях над величиной y_u при некотором наборе значений v _{1 u} , v _{2 u} , …, v_ku, получаемая оценка дисперсии среднего значения не будет отличаться от оценки дисперсии, полученной при многократных наблюдениях для любого другого набора значений независимых переменных v _{1 s} , v _2s, …, v_ks.

Указанные допущения позволяют использовать для расчетов коэффициентов полинома МНК, который дает эффективные и несмещенные оценки коэффициентов и обеспечивает простоту проведения самих расчетов. Применение МНК, вообще говоря, не требует соблюдения нормального распределения результатов наблюдения. Этот метод в любом случае дает решение, минимизирующее сумму квадратов отклонений результатов наблюдения от значений функции отклика. Допущение о нормальном распределении используется при проведении различного рода проверок, например, при проверке адекватности функции отклика и экспериментальных данных. Естественно, что точность оценок коэффициентов функции отклика повышается с увеличением числа опытов, по которым вычисляются коэффициенты.

Дата добавления: 2014-12-27