Упражнения. 1. Нарисовать диаграммы всех деревьев с 7 вершинами

1. Нарисовать диаграммы всех деревьев с 7 вершинами.

2. Допустим, что в ордереве все узлы, кроме листьев, имеют одну и ту же по­лустепень исхода n. В этом случае говорят, что дерево имеет постоянную ширину ветвления п. Оценить высоту h ордерева, которое имеет р узлов и постоянную ширину ветвления n.

Глава 8. Нечеткие множества

Определения

Пусть E - универсальное множество, x - элемент E, а R - некоторое свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар

A = {m _A (х) / х },

где m_A(х) - характеристическая функция, принимающая значение 1, если x удовлетворяет свойству R, и 0 - в противном случае.

Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "да-нет" относительно свойства R. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар A = {m_A(х)/ х }, где
m_A(х) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве M (например, M = [0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называют множеством принадлежностей. Если M = {0,1}, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.

Пример

Пусть E = { x ₁, x ₂, x ₃, x ₄, x ₅}, M = [0,1]; A - нечеткое множество, для которого m_A(x ₁)=0,3; m_A(x ₂)=0; m_A(x ₃)=1; m_A(x ₄)=0,5; m_A(x ₅)=0,9. Тогда A можно представить в виде:

A = {0,3/ x ₁; 0/ x ₂; 1/ x ₃; 0,5/ x ₄; 0,9/ x ₅ }

или

A = 0,3/ x ₁ + 0/ x ₂ + 1/ x ₃ + 0,5/ x ₄ + 0,9/ x ₅.

Пример

Пусть E = { 0,1,2,3,..., n,... }. Нечеткое множество " малый " можно определить:

" малый " =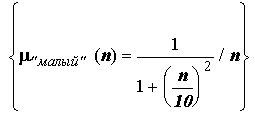

Операции над нечеткими множествами

Включение. Пусть A и B - нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если " x Î E m _A (x) m _B (x). Обозначение: A Ì B. Иногда используют термин " доминирование ", т.е. в случае когда A Ì B, говорят, что B доминирует A.

Равенство. A и B равны, если " xÎE m _A (x) = m _B (x). Обозначение: A = B.

Дополнение. Пусть M = [0,1], A и B - нечеткие множества, заданные на E. A и B дополняют друг друга, если " xÎE m _A (x) = 1 - m _B (x). Обозначение: B = или A = .

(Дополнение определено для M = [0,1], но очевидно, что его можно определить для любого упорядоченного M).

Пересечение. A Ç B - наибольшее нечеткое подмножество, содержащееся одновременно в A и B.

m _{A Ç B} (x) = min(m _A (x), m _B (x)).

Объединение. А È В - наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:

m _{A È B} (x) = max(m _A (x), m _B (x)).

Разность. А - B = А Ç с функцией принадлежности:

m _{A - B} (x) = m_{A Ç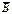} (x) = min(m _A (x), 1 - m _B (x)).

Дизъюнктивная сумма.

АÅB = (А - B)È(B - А) = (А Ç ) È( Ç B)

с функцией принадлежности:

m _{A - B} (x) = max{[min{m _A (x), 1 - m _B (x)}];[min{1 - m _A (x), m _B (x)}] }

Примеры

Пусть:

A = 0,4/ x ₁ + 0,2/ x ₂+0/ x ₃+1/ x ₄;

B = 0,7/ x ₁+0,9/ x ₂+0,1/ x ₃+1/ x ₄;

C = 0,1/ x ₁+1/ x ₂+0,2/ x ₃+0,9/ x ₄.

Здесь AÌB, т.е. A содержится в B или B доминирует A, С несравнимо ни с A, ни с B, т.е. пары {A, С} и {A, С} - пары недоминируемых нечетких множеств.

A ¹ B ¹ C.

= 0,6/ x ₁ + 0,8/ x ₂ + 1/ x ₃ + 0/ x ₄;

= 0,3/ x ₁ + 0,1/ x ₂ + 0,9/ x ₃ + 0/ x ₄.

A Ç B = 0,4/ x ₁ + 0,2/ x ₂ + 0/ x ₃ + 1/ x ₄.

А È В = 0,7/ x ₁ + 0,9/ x ₂ + 0,1/ x ₃ + 1/ x ₄.

А - В = АÇ = 0,3/ x ₁ + 0,1/ x ₂ + 0/ x ₃ + 0/ x ₄;

В - А = Ç В = 0,6/ x ₁ + 0,8/ x ₂ + 0,1/ x ₃ + 0/ x ₄.

А Å В = 0,6/ x ₁ + 0,8/ x ₂ + 0,1/ x ₃ + 0/ x ₄.

Алгебраическое произведение A и B обозначается A×B и определяется так:

" x ÎE m _{A × B} (x) = m _A (x)m _B (x).

Алгебраическая сумма этих множеств обозначается A+B и определяется так:

" xÎE m _A+B (x) = m _A (x) + m _B (x) - m _A (x)m _B (x).

На основе операции алгебраического произведения (по крайней мере для целых a эта основа очевидна) определяется операция возведения в степень a нечеткого множества A, где a - положительное число. Нечеткое множество A^a определяется функцией принадлежности m_A^a = m^a _A (x). Частным случаем возведения в степень являются:

CON(A) = A² - операция концентрирования,

DIL(A) = A^0,5 - операция растяжения.

Расстояние между нечеткими множествами

Расстояние Хемми нга (или линейное расстояние):

r(A, B) = 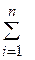½m _A (x_i) - m _B (x_i)½.

Очевидно, что r(A, B)Î[0, n ].

Евклидово или квадратичное расстояние:

e(A, B) = 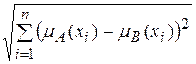, e(A, B)Î[0, ].

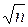Глава 9. Теория алгоритмов

Дата добавления: 2014-12-27