Алгоритмическая разрешимость

Рекурсивные функции

Алгоритм ставит в соответствие входным данным выходные, следовательно, с каждым детерминированным алгоритмом можно однозначно сопоставить функцию, которую он вычисляет.

Функция, области определения и значений которой есть множество натуральных чисел, называется вычислимой, если существует машина Тьюринга, которая реализует процесс вычисления значений этой функции.

Попытки описать такие вычислимые функции привели к созданию теории рекурсивной функции.

Рекурсия – это способ задания функций на множестве натуральных чисел, при которых значение функции для произвольного значения аргумента выражаются через значение этой функции при меньшем значении аргумента.

Пример

Рекурсивная функция для вычисления факториала (f (z) = n!):

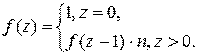
Пример

Рекурсивная функция для вычисления набольшего общего делителя пары чисел (a, b):

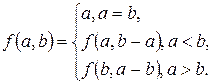
Возникает вопрос: существует ли какая-либо стандартная форма алго­ритма, решающая данный класс задач? В ряде случаев на этот вопрос теория алгоритмов дает отрицательный ответ.

Пример

Доказана неразре­шимость ряда задач: невозможность решения в радика­лах алгебраических уравнений выше четвертой степени, невозмож­ность трисекции угла с помощью циркуля и линейки и т. п.

Алгоритмическую неразрешимость следует понимать в том смыс­ле, что не существует единого алгоритма для решения проблемы в целом. Но это вовсе не означает неразрешимость более узких классов задач данной проблемы.

С точки зрения инженерной практики проблема алгоритмичес­кой разрешимости выглядит совсем иначе, чем с позиций самой мате­матики. В силу конечности реального времени, отводимого на реше­ние задачи, и ограниченных возможностей средств вычислительной техники даже простые алгоритмы могут оказаться практически нереализуемыми, если они требуют выполнения слишком большого числа операций.

Пример

Задачи выбора оптимальных вариантов при про­ектировании, игровые задачи и алгоритмы, основанные на простом переборе и т. п.

Но в то же время алгоритмическая неразрешимость проблемы в целом не является препятствием для решения частных задач, относящихся к этой проблеме.

Пример

Среди алгебраических уравнений выше четвертой степени могут оказаться такие, которые решаются не только в радикалах, но и в целых числах. Более того, можно определить корни уравнения с достаточной для прак­тики степенью приближения, вовсе отказавшись от стремления найти решение в радикалах.

Аналогичный подход выработала практика и к задачам, которые относятся к нерешенным проблемам.

Пример

До сих пор не най­ден общий алгоритм раскраски граней любого плоского графа не больше чем четырьмя различными цветами так, чтобы никакие соседние грани не были окрашены одинаковым цветом (проблема четырех красок). В то же время в реальных условиях еще не встре­чалось случаев, когда такая раскраска оказалась бы невозможной (изготовление географических карт).

В отличие от алгоритмов, практические способы, исполь­зуемые для решения таких задач, относящихся к нерешенным проб­лемам, называют псевдоалгоритмами.

Дата добавления: 2014-12-27