Разложение функции в полином

ВТОРАЯ ФОРМА

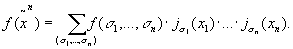
Задание 3. Представить данные функции во второй форме:

а)

б)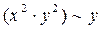

в)

г)

Например, 1) 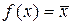. Пусть k = 3, E_k=={0,1,2}

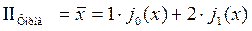
2)

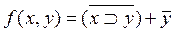
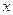
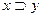
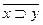
Теорема. Любая функция и P_k представима многочленом по mod k тогда и только тогда, когда k – простое число.

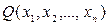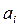Опр. Многочленом по mod k от переменных называется выражение вида , где коэффициенты принадлежат множеству есть либо некоторая переменная из , либо произведение переменных из этого множества.

Например. Если k=3 и , то стандартный вид разложения функции от одной переменной в полином имеет вид: 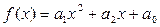_, а если k=5 и 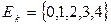, то

Если функция от двух переменных, то при k=3 полином имеет вид:

x1	j2(x)

Пример 1. Разложить в полином функцию f(x) = ~ x при k=5 методом неопределённых коэффициентов.

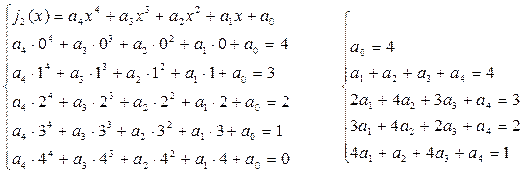
Решим систему методом Гаусса

Итак, f(x) = ~ x = 4 + 4x

Функцию из P_k (k – простое число) можно разложить в полином, используя вторую форму разложения функции, в силу того, что при k = p (где p – простое число).

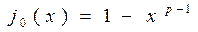, т.е.

Пример 2 Разложить функцию 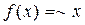в полином, используя вторую форму.

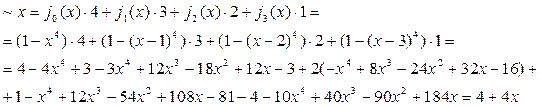
Аналогично раскладываются функции от двух переменных из P_k в полином.

Пример 3. Разложить в полином функцию Вебба методом неопределённых коэффициентов и через вторую форму. Пусть k=3 E_k={0,1,2}

x	y	V3=max(x,y)+1

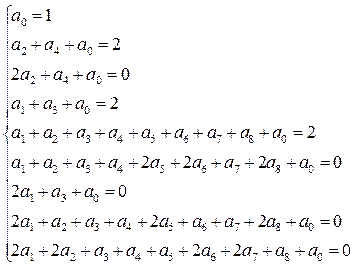
Решив систему уравнений, получим:

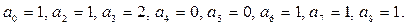
Итак, данная функция в виде полинома имеет вид:

Разложим функцию V₃ в полином через вторую форму:

, где

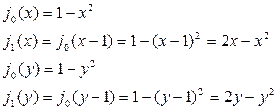
Отсюда

Пример 4. Разложить данные функции в полином при k = 3, 5, 7:

а)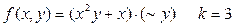

б)

в)

г)

При разложении берем те значения переменных, при которых значение функции не равно нулю.

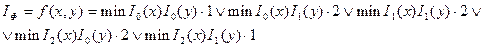
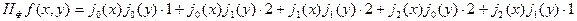
1.

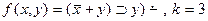
2.

3.

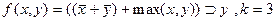
4.

5.

6.

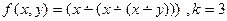
7.

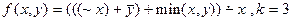
8.

9.

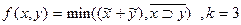
10.

11.

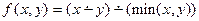
12.

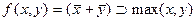
13.

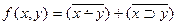
14.

Пример 5. Доказать справедливость следующих соотношений:

а) б)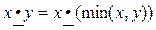

При доказательстве справедливости данных соотношений следует доказать, что левая часть равна правой, или правая равна левой, или левая и правая части равны какому-либо одному соотношению.

Решение:

а)

б) 1. пусть x ≥ y

2. пусть x < y

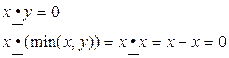
Пример 6. Доказать:

а)

б)

в)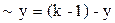

г)

д)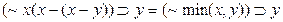

6. Полные системы функций в P_k

Определение. Система называется полной, если любая функция из P_k может быть записана в виде формулы от функций данной системы.

Примеры полных систем.

1. H= P_k полна
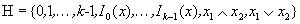2. система Россера-Туркетта

Эта система полна. Покажем это.

Доказательство: Пусть 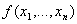- произвольная функция из P_k

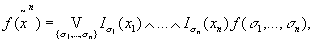
Данная формула построена из функций, входящих в Н.

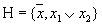1. в P_k полна (система Поста).

Покажем, что Н полна методом сведения к полной системе Россера-Туркетта.

Доказательство:

а) построение констант.

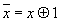
x+2=(x+1)+1,…,x+(k-1)=(x+(k-2)+1,

x=x+k=(x+(k-1))+1

Тогда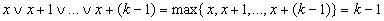

Следовательно, при помощи 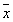получаем остальные const.

б) построение функций одной переменной.

Сначала получим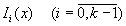

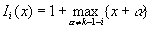
Проверим это:

1)

I_i (x)= k -1

2)

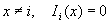
Введём функцию

Покажем, что

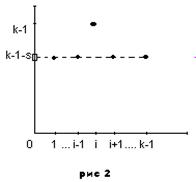
Рис 1 - I_i (x) Рис 2 - max(I_i (x), k -1- s) Рис 3 - s +1+max(I_i (x), k -1- s)

Если f (x) - произвольная функция одной переменной из P_k, то

в частности

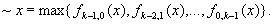
в) получение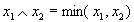

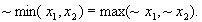
Отсюда

Т.о., при помощи формул над исходной системой функций выразить любую из функций системы Россера-Туркетта, относительно которой доказано, что она полная.

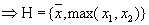- полна.

(4) 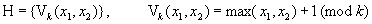(функция Вебба представляет собой функции Шеффера).

Эта система полна

Вопрос о её полноте сводится к полноте системы 3.

(5)

7. Замкнутые системы в P_k

Определение. . Замыканием Н называется множество [H] всех функций из P_k, представимых в виде формул через функции множества Н.

Определение. Класс Н называется замкнутым, если [H]=H.

Примеры

1. Н= P_k - замкнутый класс.
2. Пусть

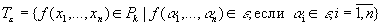
- множество всех функций, сохраняющих a, т.е.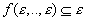

- класс сохранения множества e.

Класс Н= - замкнут, т.к. [ ]=

Другое определение полноты. Н - полная система, если [H]= P_k

Понятие замкнутого класса может быть приложено к решению вопроса об обосновании неполноты некоторых систем.

Пример. . Пусть

~ x, max(x ₁, x ₂) - сохраняют e

Т.к. при не содержит 1. Значит при 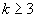Н не будет полной системой.

Т.е. хотя Н обобщение системы 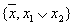булевых функций, она не является полной.

Рекомендуемая литература:

Основная:

1. Яблонский С.В. Введение в дискретную математику /С.В.Яблонский – М.:Наука, 1979г. 272 с.
2. Новиков Ф.А. Дискретная математика для программистов/ Ф.А Новиков – СПб: Питер, 2000. – 304 с.
3. Нефедов В.Н., Осипова В.А. Курс дискретной математики / В.Н. Нефедов, В.А. Осипова – М.: изд-во МАИ, 1992г. 264 с.
4. Карпов В.Г., Мощенский В.А. Математическая логика и дискретная математика./ В.Г. Карпов, В.А. Мощенский – Минск, 1977г. 256 с.
5. Гаврилов Г.П., Сапоженко В.А. Сборник задач по дискретной математике / Г.П. Гаврилов, В.А. Сапоженко – М.: Наука, 1977 г. 368 с.
6. Емеличев В.А.Лекции по теории графов / В.А. Емелечев, О.И.Мельников, В.И Сарванов., Р.И.Тышкевич – М.: Наука, 1990г. 384 с.
7. Грэхем Р. Конкретная математика. Основы информатики / Р.Грэхем, Д.Кнут, О. Паташник: Пер. С англ. – М.: Мир, 1998. – 703 с.
8. Кнут Дональд, Эрвин. Искусство программирования, том 1. Основные алгоритмы / Дональд, Эрвин Кнут, 3-е изд.: Пер. с англ.: Уч. пос. – М.: Издательский дом «Вильямс», 2000. – 720 с.
9. Кнут Дональд, Эрвин. Искусство программирования / Дональд, Эрвин Кнут, том 2. Получисленные алгоритмы, 3-е изд.: Пер. с англ.: Уч. пос. – М.: Издательский дом «Вильямс», 2000. – 832 с.
10. Кнут Дональд, Эрвин. Искусство программирования / Дональд, Эрвин Кнут, том 3. Сортировка и поиск, 2-е изд.: Пер. с англ.: Уч. пос. – М.: Издательский дом «Вильямс», 2000. – 832 с.

Дополнительная:

1. Яблонский С.В., Функции алгебры логики и классы Поста. / С.В. Яблонский, Г.П.Гаврилов, В.Б.Кудрявцев – М.: Наука, 1966г. 304 с.
2. Гиндикин С.Г. Алгебра логики в задачах./ С.Г.Гиндикин – М.: Наука, 1972г. 324 с.
3. Донской В.И. Дискретная математика / В.И. Донской. – Симферополь: «СОНАТ», 2000. 340 с.
4. Epp, S. S., Discrete Mathematics with Applications, 2nd edition, PWS Publishing Company, 1995.
5. Rosen, K.H., Discrete Mathematics & Its Applications, 3rd edition, McGraw-Hill, 1995.
6. Aho, A.V., and Ullman, J.D., Foundations of Computer Science, Computer Science Press 1992.
7. Grimaldi, R.P., Discrete & Combinatorial Mathematics, 3rd edition, Addison-Wesley, 1994.
8. Johnsonbaugh, R., Discrete Mathematics, Revised edition, Macmillan, 1989.
9. Ross, K.A., and Wright, C.R.B., Discrete Mathematics, 3rd edition, PHI, 1992. ISBN 0-13-215716-0.
10. Albertson, M.O., and Hutchinson, J.P., Discrete Mathematics with Algorithms, Wiley, 1988. ISBN 0-471-61278-2.
11. Dromey, R.G. How to solve it by computer, PHI, 1982. ISBN 0-13-433995-9.
12. Dromey, R.G. Program Derivation, Addison-Wesley, 1989. ISBN 0-201-41624-7.
13. Reingold, E.M., Nievergelt, J., And Deo, N., Combinatorial algorithms, PHI. ISBN 0-13-152447-X.

Приложение

Содержание дисциплины «Дискретная математика» для студентов заочной формы обучения

I семестр

Основные понятия. Элементарные булевы функции. Существенные и фиктивные переменные.

Логические формулы. Реализация функций формулами. Эквивалентность формул. Основные свойства элементарных функций.

Двойственные функции. Основные свойства двойственных функций. Самодвойственные функции.

Разложение булевых функций по переменным. Совершенная дизъюнктивно нормальная форма(СДНФ). Совершенная конъюнктивно нормальная форма(СКНФ).

Представление функции посредством полинома Жегалкина. Линейные функции.

Полные системы. Первый критерий функциональной полноты.

Замкнутые системы. Свойства замкнутых множеств. Замыкание множества.

Важнейшие замкнутые классы. Класс функций, сохраняющих 0, класс функций, сохраняющих 1. класс монотонных функций, класс самодвойственных функций, класс линейных функций.

Критерий функциональной полноты (теорема Поста). Предполные классы. Теорема о существовании 5 предполных классов.

Проблема минимизации булевых функций.Элементарная конъюнкция, ранг элементарной конъюнкции, д.н.ф. Индекс простоты, минимальная д.н.ф., кратчайшая д.н.ф.

Упрощение д.н.ф. и способы построения тупиковых д.н.ф.

Проблема минимизации булевых функций на основе геометрических представлений. Грань, носитель, интервал.

Сокращенная д.н.ф.

Тупиковые д.н.ф. на основе геометрических представлений. Построение т.д.н.ф. табличным способом.

k-значная логика.Функции k-значной логики. Формулы и реализация функций формулами. Элементарные функции. Свойства элементарных функций. Первая и вторая формы. Представление функций k-значных логик формулами специального вида.

Полные системы. Система Россера-Туркетта. Система Поста. Функция Вебба. Представление функций полиномами. Малая теорема Ферма.

Исследование систем k-значной логики на полноту. Алгоритм распознавания полноты. Теорема о полноте.

Особенности k-значных логик.

II семестр

Теория графов.Основные понятия. Определение графа. Степень вершин графа. “Лемма о рукопожатиях”. Двудольные графы. Изоморфные графы.

Подграфы. Операции над графами. Объединение графов. Дизъюнктное объединение графов.

Произведение. Операции слияния вершин, стягивания ребер, удаления и расщепления вершины.

Циклы, цепи и компоненты. Марширут, соединяющий вершины. Обхват графа. Свойства цепей и циклов. Ориентированный маршрут, ориентированная цепь. Теорема о числе ребер графа.

Матрицы, ассоциированные с графом. Бинарная матрица. Матрица смежности графа. Теорема об изоморфности графа. Характеристический полином графа. Спектр графа. Матрица Кирхгофа. Матрица инцидентности.

Метрические характеристики графа. Расстояние между вершинами. Аксиомы метрики. Эксцентриситет, диаметр. Периферийная вершина. Диаметральная цепь. Радиус.

Критерий двудольности графа. Теорема Кенига. Поиск в ширину.

Определение дерева. Ациклический граф (лес). Теорема об эквивалентности нескольких вариантов определения дерева. Теорема о концевых вершинах дерева.

Вершинная и реберная связность графа.Число вершинной связности. Число реберной связности. Точка сочленения. Мост. Теорема о соотношении между степенью графа, числами вершинной и реберной связности. Теорема о существовании графа с заданными степенью графа, числами вершинной и реберной связности. Теорема об общих вершинах двух компонент графа.

Двусвязные графы. Простые свойства двусвязных графов. Теорема о двусвязном графе. Блоковые множества. Структура графа с точностью до блоков. Концевые блоки. Трехсвязные графы. Структура графа с точностью до листа.

Плоские и планарные графы. Стереографическая проекция. Укладка графа в заданное пространство и на сферу.

Грани плоского графа. Граница грани. Внутренняя и внешняя грань. Свойства плоских укладок графа. Формула Эйлера. Теоремы о непланарных графах.

Критерий планарности графа. Критерий планарности трехсвязных графов.

Алгоритм укладки графа на плоскости. Сегмент, контактная вершина, допустимая грань для данного сегмента. Конфликтующие сегменты. Обоснование алгоритма укладки графа на плоскости. Частичная укладка планарного графа.

Эйлеровы графы. Эйлеровый цикл. Теорема Эйлера. Алгоритм Флери.Покрытие графа реберно непересекающимися цепями. Теорема о минимальном числе реберно непересекающихся цепей.

Гамильтоновы графы. Гамильтоновый цикл. Тэта-подграф. Теорема о негамильтоновом двусвязном графе.

Теория кодирования.Основные понятия. Способы описания источников сообщения. Код сообщения. Схема кодирования. Алфавитное кодирование. Равномерное кодирование. Способы описания источника помех. Декодирование. Критерий однозначности декодирования. Свойство префикса.

Алгоритм распознавания однозначности декодирования.

Код Шеннона. Кодирование и декодирование.

Коды с минимальной избыточностью. Избыточность кодирования. Кодовое дерево. Два преобразования кодовых деревьев, не увеличивающих избыточность. Коды Хафмана. Редукция.

Самокорректирующиеся коды. Коды Хэмминга. Построение кодов Хэмминга. Информационные и контрольные разряды. Обнаружение ошибки. Декодирование. Геометрические свойства кодов Хэмминга.

Перечень вопросов к экзаменационным билетам:

1. Функции алгебры логики. Основные понятия. Элементарные булевы функции.

2. Способы задания булевых функций. Фиктивные и существенные переменные.

3. Логическая формула. Основные свойства элементарных булевых функций.

4. Совершенная дизъюнктивная нормальная форма. Теорема о представлении булевых функций в СДНФ.

5. Совершенная конъюнктивная нормальная форма. Представление булевых функций в СКНФ.

6. Полные системы функций в Р₂. Первый критерий функциональной полноты.

7. Полином Жегалкина. Теорема о представлении функции полиномом Жегалкина.

8. Замкнутые системы функций в Р₂. Свойства замкнутых систем и замыканий.

9. Класс функций, сохраняющих 0. Класс функций, сохраняющих 1.

10. Класс самодвойственных функций. Лемма о несамодвойственной функции.

11. Класс монотонных функций. Лемма о немонотонной функции.

12. Класс линейных функций. Лемма о нелинейной функции.

13. Теорема Поста (Критерий функциональной полноты).

14. Следствия из теоремы Поста.

15. Предполные классы в Р₂.

16. Проблема минимизации булевых функций. Индекс простоты.

17. Тупиковые ДНФ. Способы упрощения ДНФ.

18. Проблема минимизации булевых функций на основе геометрических представлений.

19. Сокращенная ДНФ.

20. ТДНФ на основе геометрических представлений.

21. Введение в k-значную логику. Элементарные функции k-значной логики.

22. Представление функций k-значной логики в первую и вторую формы.

23. Полные системы в Р_k. Примеры полных систем.

24. Замкнутые системы в Р_k. Примеры замкнутых систем.

25. Представление функций в Р_k полиномом по модулю k.

26. Задача распознавания полноты в Р_k. Алгоритмический подход.

27. Задача распознавания полноты в Р_k. Подход, связанный с проверкой некоторых свойств системы функций.

28. Основные понятия теории графов. Виды графов. Двудольные графы.

29. Операции над графами.

30. Изоморфизм графов.

31. Дополнительный граф.

32. Цепи. Циклы. Компоненты.

33. Связанные графы. Свойства связанных графов.

34. Критерий двудольности графа. Теорема Кенига.

35. Метод поиска в ширину.

36. Матрицы, ассоциируемые с графом.

37. Деревья. Теорема о дереве. Следствия.

38. Остов графа.

39. Вершинная и реберная связность графа. Теорема о соотношении между числами: минимальной степени вершин графа, числами реберной и вершинной связности графа.

40. Утверждение о построении графа с заданными числами: минимальной степени вершин графа, числами реберной и вершинной связности графа.

41. Двусвязные графы. Теорема о двусвязном графе.

42. Трехсвязные графы. Теорема о трехсвязном графе.

43. Плоские и планарные графы. Теорема об укладке графа в трехмерное пространство.

44. Теорема об укладке графа на сфере.

45. Грани плоского графа. Утверждение о преобразовании внутренней грани во внешнюю.

46. Формула Эйлера. Следствия из теоремы Эйлера.

47. Свойства плоских укладок графа.

48. Алгоритм укладки графа на плоскости.

49. Эйлеровы графы. Теорема Эйлера.

50. Реберно-непересекающиеся цепи. Следствие из теоремы Эйлера о минимальном числе покрывающих граф цепей.

51. Алгоритм построения эйлерова цикла (алгоритм Флери).

52. Элементы теории кодирования. Основные понятия и определения.

53. Достаточный признак однозначности декодирования.

54. Код Шеннона.

55. Код Хемминга.

Дата добавления: 2014-12-27