И.А. Ковалькова 1 страница

0 2 1

Существуют разные правила для перевода целых и дробных чисел.

Правила перевода целых чисел.

Чтобы перевести целое число из десятичной системы счисления в двоичную (шестнадцатеричную) систему счисления, необходимо исходное число разделить на основание новой системы счисления (два или шестнадцать). Полученное частное вновь делится на основание и так до тех пор, пока частное не станет меньше основания новой системы счисления. Последнее частное будет первой цифрой в числе новой системы счисления. Последующие цифры в новом числе будут соответствовать остаткам в обратном порядке их получения.

Пример: перевести целое число 24 из десятичной системы счисления в двоичную систему счисления.

(24)₁₀ – (?)₂

24 2

24 12 2 Таким образом получается число: (11000 )2.

0 12 6 2

0 6 3 2

Пример: перевести целое число 24 из десятичной системы счисления в шестнадцатеричную систему счисления. (24)₁₀ –(?)₁₆

24 16

16 1 Получается число (18)₁₆.

Правила перевода дробной части числа.

Если дробь неправильная – целая и дробная часть переводится по своим правилам.

Чтобы перевести правильную дробь издесятичной системы счисления в двоичную (шестнадцатеричную) систему счисления, необходимо исходную дробь умножить на основание новой системы счисления. В полученном произведении выделяется целая и дробная части. Дробная часть умножается на основание новой системы.

Цифры в новой системе счисления соответствуют целым частям произведения в порядке их получения.

Пример: перевести правильную дробь 0, 35 из десятичной системы счисления в двоичную систему счисления. (0,35)₁₀ –(?)₂

0,35*2= 0,7; 0,7*2= 1,4; 0,4*2= 0,8; 0,8*2= 1,6; 0,6*2= 1,2; 0,2*2= 0,4;…

Таким образом, получается число (0,010110…) ₂

Пример: перевести правильную дробь 0, 35 из десятичной системы счисления в шестнадцатеричную систему счисления. (0.35)₁₀ – (?)₁₆

0.35 0.6 0.6

* 16 *16 *16

5. 6 9. 6 9. 6

Получается число (0,59…9)₁₆

Правила перевода из двоичной системы счисления в шестнадцатеричную систему счисления.

Чтобы перевести число из двоичной системы счисления в шестнадцатеричную систему счисления, необходимо, двигаясь вправо и влево от запятой, разбить число на тетрады. Каждую тетраду необходимо заменить шестнадцатеричной системой счисления (см.таблицу1), недостающие разряды добавляются нулями.

Пример: перевести число 11000, 01011 из двоичной системы в шестнадцатеричную систему счисления

(00011000,01011000)₂ – (?)₁₆

1 8, 5 8

Получается число (18,58)₁₆

Правила перевода из шестнадцатеричной системы счисления в двоичную систему счисления.

Чтобы перевести число из шестнадцатеричной системы счисления в двоичную систему счисления необходимо каждую шестнадцатеричную цифру заменить эквивалентной тетрадой в двоичной системе счисления (см. таблицу 1).

Пример: перевести число 18,59 из шестнадцатеричной системы счисления в двоичную систему счисления.

(18,59)₁₆ – (?)₂

1 8, 5 9

0001 1000, 0101 1001

Получается число ( 11000,01011001)₂.

Задание 1.

Перевести число А из десятичной системы счисления в двоичную и шестнадцатеричную систему счисления.

Полученные числа перевести в десятичную систему счисления.

Перевести число А из двоичной системы счисления в шестнадцатеричную систему счисления. И обратно, из шестнадцатеричной системы счисления в двоичную систему счисления.

Перевести число В из десятичной системы счисления в двоичную систему счисления. И обратно, из двоичной системы счисления в десятичную систему счисления. Числа А и В приведены в таблице 2.

Таблица 2.

Номер варианта	А	В

Прямой, обратный, дополнительный коды.

Прямой код числа.

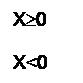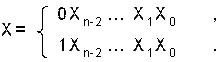Прямым кодом целого числа x является число, образованное по формуле:

где n-1 – число значащих разрядов в числе

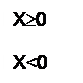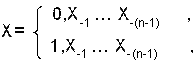Для дробного числа:

В дальнейшем, для наглядности, знаковый разряд отделяется точкой:

0. 101

Знаковый разряд Значащие разряды

1. 101

Обратный код числа.

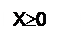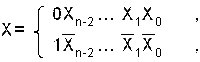Обратным кодом целого числа x является число, образованное по формуле:

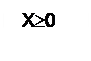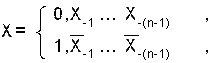Д ля дробного числа:

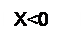X_i – это дополнение до основания системы счисления.

Для двоичной системы счисления обратный код отрицательного числа получается путём инвертирования значащих разрядов, т.е. нули заменяются единицами и наоборот - единицы нулями, а в знаковый разряд ставится 1.

Пример:

0.101 +5 прямой код

1.010 -5 обратный код

Примечание: Для положительных чисел прямой и обратный код совпадают.

Действия с использованием обратного кода

При использовании алгебраического суммирования отрицательные числа представляются в обратном коде, положительные – в прямом и производится поразрядное суммирование, включая знаковый разряд.

Если возникает единица переноса из знакового разряда, то она подсуммируется к младшему разряду.

Если знаковый разряд суммы равняется “0”, то это означает, что результат положительный и представлен в прямом коде.

Если в знаковом разряде суммы единица, то это означает, что результат отрицательный и представлен в обратном коде.

Пример:

А=5, В=4

0.0101 +5 прямой код 0.0100 +4 прямой код

1.1010 -5 обратный код 1.1011 -4 обратный код

А+В

+

0.0101 +5 прямой код

0.0100 +4 прямой код

0.1001 +9 прямой код

А-В

+

0.0101 +5 прямой код

1.1011 -4 обратный код

1 0.0000

+1

0.0001 прямой код

Знаковый разряд результата равен 0. Из этого следует, что результат положительный и представлен в прямом коде.

В-А

+

0.0100 +4 прямой код

1.1010 -5 обратный код

1.1110

Знаковый разряд результата равен 1. Следовательно, результат получается отрицательным и представлен в обратном коде. Прямой код результата равен:

1.0001 прямой код

Дополнительный код числа

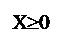Дополнительным кодом целого числа x является число, образованное по формуле:

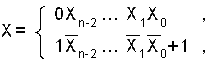Д ля дробного числа:

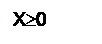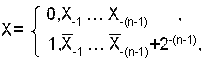Положительное число в прямом и дополнительном коде совпадают.

Чтобы получить дополнительный код целого отрицательного двоичного числа необходимо проинвертировать значащую часть и прибавить “1” к младшему разряду, в знаковый разряд поставить 1.

Пример:

А=5, В=4

+

+

1.1010 -5 обратный код 1.1011 -4 обратный код

1 1

1.1011 -5 дополнительный код 1.1100 -4 дополнительный код

Действия с использованием дополнительного кода

При алгебраическом суммировании с использованием дополнительного кода, отрицательные числа представляются в дополнительном коде, а положительные – в прямом коде и производится суммирование кодов чисел, включая знаковый разряд.

При возникновении единицы переноса из знакового разряда, эта единица отбрасывается в отличие от обратного кода.

Пример:

А-В

+

1.1100 -4 дополнительный код

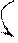
0.0101 +5 прямой код

0.0001 +1 прямой код

Если образовался “0” в знаковом разряде, то число получилось положительным и представлено в прямом коде, а если “1”, то это число отрицательное и представлено в дополнительном коде.

Пример:

В-А

+

0.0100 +4 прямой код

1.1011 -5 дополнительный код

1.1111

Знаковый разряд результата равен 1. Из этого следует, что результат получился отрицательным и представлен в дополнительном коде. Прямой код результата равен:

+

1.0000

1

1.0001 -1 прямой код

Переполнение разрядной сетки.

Переполнением разрядной сетки называется ситуация, когда при суммировании кодов чисел результат требует на один разряд больше, чем исходные операнды и не умещается в разрядной сетке ЭВМ.

Признаки переполнения разрядной сетки ЭВМ.

1) По наличию и отсутствию переноса в знаковый и из знакового разряда

Переполнение возникает в том случае, если существует только лишь один перенос, либо в знаковый разряд, либо из знакового разряда. Если существуют оба переноса и в знаковый разряд и из знакового разряда, либо переносы из знакового и в знаковый разряды отсутствуют, то переполнения разрядной сетки нет.

Пример:

А=5, В=4

0.101 +5 прямой код 0.100 +4 прямой код

1.010 -5 обратный код 1.011 -4 обратный код

А+В

1

+

+

0.101 +5 прямой код

0.100 +4 прямой код

1.001 переполнение!!!

Имеется один перенос в знаковый разряд, перенос из знакового разряда отсутствует.

-А-В

1

+

1.010 -5 обратный код

1.011 -4 обратный код

0.101 переполнение!!!

Имеется один перенос из знакового разряда, перенос в знаковый разряд отсутствует.

2)Модифицированное кодирование.

Модифицированным кодом называется код, в котором под знак числа отводится два или более разрядов.

При использовании двух разрядов для представления знака числа комбинация знаковых разрядов 00 соответствует положительным числам, комбинация 11 – отрицательным числам, комбинации 01 и 10 соответствуют переполнению разрядной сетки.

Пример:

А+В

+

00.101 +5 прямой модифицированный код

00.100 +4 прямой модифицированный код

01.001 переполнение!!!

Комбинация 01 в знаковом разряде соответствует переполнению разрядной сетки.

(-А)+(-В)

+

11.010 -5 обратный модифицированный код

11.011 -4 обратный модифицированный код

10.101 переполнение!!!

Комбинация 10 в знаковом разряде соответствует переполнению разрядной сетки.

Пример для дополнительного модифицированного кода:

А-В

+

00.101 +5 прямой модифицированный код

11.100 -4 дополнительный модифицированный код

00.001 +1 прямой код

В знаковых разрядах результата комбинация 00.Из этого следует, что переполнение разрядной сетки отсутствует, результат положительный.

В-А

+

00.100 +4 прямой модифицированный код

11.011 -5 дополнительный модифицированный код

11.111

В знаковых разрядах результата комбинация 11.Из этого следует, что переполнение разрядной сетки отсутствует и результат отрицательный, представлен в дополнительном коде.

+

111.000

1

11.001 -1 прямой код

(-А)+(-В)

+

11.011 -5 дополнительный модифицированный код

11.100 - 4 дополнительный модифицированный код

10.111 переполнение!!!

В знаковых разрядах результата комбинация 10,что соответствует переполнению разрядной сетки.

Задание 2.

Вычислить в обратном модифицированном коде А-В; В-А

Вычислить с использованием дополнительного модифицированного кода А-В;В-А.

Вычислить А+В с помощью:

а) модифицированного кодирования,

б) определить переполнение разрядной сетки ЭВМ по наличию и отсутствию переноса в знаковый и из знакового разряда соответственно.

Число значащих разрядов в числе равно 5. Числа А и В приведены в таблице 1(см. задание 1).

Формы представления чисел в ЭВМ.

Формат представления чисел с фиксированной точкой.

np

Знак (n-1)p- значащие разряды числа

Точка может фиксироваться либо перед старшим разрядом числа, либо после младшего. Если точка фиксируется перед старшим разрядом числа, то все числа по модулю меньше единицы. Если после младшего, то все числа по модулю больше единицы.

В современных ЭВМ для представления целых чисел используется формат чисел с фиксированной точкой, причем точка фиксируется после младшего разряда.

Замечание. Отрицательные числа с фиксированной точкой хранятся в памяти в обратном или в дополнительном коде.

Формат чисел с плавающей точкой.

Х= ± Мх*q ^{± px}

Где Мх – мантисса числа,

q - основание системы счисления,

p - порядок

Мантисса - это нормализованная правильная дробь.

Знак знак Pх мх- мантисса числа

числа порядка порядок числа

Рсм = Рх + 2^L – смещенный порядок,

где L- количество разрядов, отводимое под порядок.

Примеры представления чисел в форме с плавающей точкой. Длина разрядной сетки n принимается равной 32 разряда, под смещенный порядок отводится 7 разрядов.

Пример:Число (24,35)₁₀ представить в форме с плавающей точкой.

(24,35)₁₀ – (18,59…9)₁₆ Px =2

Рсм = (42)₁₆ = (66)₁₀

100 0010

0001 1000 0101 1001 1001 1001

Знак 4 2 1 8 5 9 9 9

числа

Пример:Число (38,0)₁₀ представить в форме с плавающей точкой.

(38,0)₁₀ – (26,0)₁₆ Px =2

Рсм = (42)₁₆ = (66)₁₀

100 0010

0010 0110 0000 0000 0000 0000

Знак 4 2 2 6

числа

Пример:Число (0,38)₁₀ представить в форме с плавающей точкой.

(0,38)₁₀ – (0,6С…С)₁₆ Px =0

Рсм = P_x + 2^L = 0+64 = (64)₁₀= (40)₁₆

100 0000

0110 1100 1100 1100 1100 1100

Знак 4 0 6 C C C C C

числа

Задание 3.

Число А представить в формате с фиксированной точкой. Разрядная сетка равна 16 разрядам.

Представить число в формате с плавающей точкой. Разрядная сетка равна 32 разряда, 7 разрядов – смещенный порядок, 24 разряда – мантисса числа. Числа А и В приведены в таблице 2 (см. задание 1)

а) А,0

б) 0,А

в) А,В

г)-А,В

Организация центрального процессора.

Центральный процессор (ЦП) – это устройство предназначается для непосредственной обработки данных и работает под управлением программ.

Основные узлы центрального процессора.

1) Арифметико логическое устройство (АЛУ). Предназначается для выполнения арифметических и логических операций над данными.

В АЛУ выполняются операции с фиксированной точкой; с плавающей точкой; операции двоично – десятичной арифметики, логические операции, обработка алфавитно-цифровой информации.

2) Устройство управления (УУ) – предназначается для выработки управляющих сигналов, под воздействие которых выполняются машинные команды.

Основные этапы выполнения машинной команды.

1 этап: выбор машинной команды из памяти

2 этап: дешифрация кода операции

3 этап: формирование исполнительного адреса и выбор операндов

4 этап: непосредственное выполнение операции в АЛУ

5 этап: запись результата

3)Регистры общего назначения (РОНы).

РОНы-это программно-адресуемые регистры, предназначаются для хранения операндов, результатов, а также для хранения индекса, базы, используются при вычислении адреса.

4) Управляющие регистры

Счётчик команд (СчК) – хранит адрес следующей выполняемой команды.

Регистр команд (РК) – хранит текущую выполняемую команду.

5) Вспомогательные блоки – к ним относится блок прерывания; блок связи центрального процессора (ЦП) и оперативной памяти (ОП),блок контроля и диагностики и т.д.

Организация операционной части центрального процессора.

Команды ЭВМ.

Машинная команда – это двоичный код, который включает в себя операционную часть и адресную часть.

В адресной части содержится информация об адресах операндов и результатов.

Различаются следующие команды:

4-х адресная,

3-х адресная,

2-х адресная,

одноадресная

и безадресная команды.

4-х адресные команды.

операционная адресная

часть часть

Поле А1 – адрес первого операнда

Поле А2 – адрес второго операнда

Поле А3 – адрес результата

Поле А4 – адрес следующей выполняемой команды

Микропрограмма и структурная схема операционной части ЦП при выполнении 4-х адресной команды.

Пусть А1-адрес ячейки оперативной памяти, где хранится первый операнд;

А2- адрес ячейки оперативной памяти, где хранится второй операнд;

А3- адрес ячейки оперативной памяти, по которому необходимо записать результат;

А4- адрес ячейки оперативной памяти, где хранится следующая выполняемая команда.

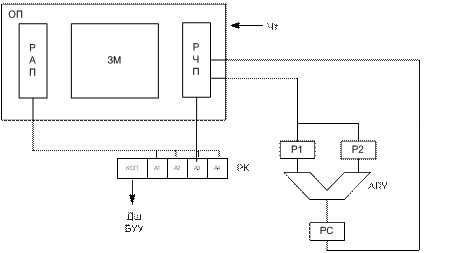
Рис. 1.

ЗМ – запоминающий массив

РАП – регистр адреса памяти

РЧП – регистр числа памяти

РК – регистр команд

АЛУ - арифметико логическое устройство

Р1, Р2-входные регистры АЛУ, предназначаются для хранения операндов

РС - выходной регистр, предназначается для хранения результата выполненной операции в АЛУ

1 этап. Выбирается команда из памяти

РАП:=РК(А4)

Адрес следующей выполняемой команды подается в память на регистр адреса памяти (РАП)

РЧП:=Чт(РАП), (в результате выполнения микрооперации на РЧП содержится сама команда)

Это непосредственный выбор самой команды из ЗМ

РК:=РЧП

Пересылается команда из памяти в ЦП на РК.

2 этап. Дешифрация кода операции.

3 этап. Формируется исполнительный адрес и выбираются операнды.

Выбор 1-го операнда

РАП:=РК(А1)

Адрес первого операнда подаётся в ОП на РАП

РЧП:=Чт(РАП)

Чтение из ЗМ на РЧП первого операнда.

Р1:=РЧП

Первый операнд подаётся на входной регистр АЛУ.

Выбор 2-го операнда

РАП:=РК(А2)

Адрес второго операнда подаётся в ОП на РАП

РЧП:=Чт(РАП)

Чтение из ЗМ на РЧП второго операнда.

Дата добавления: 2014-12-27