Пример 3.2

Группа разработчиков должна создать ИС. Существует 2 варианта:

- разработать систему с нуля. Стоимость системы 120 у.е.;

- создавать ее на основе существующей платформы. Стоимость 50 у.е.

Вероятность хорошего спроса любой информационной системы – 65%. Слабый спрос – 35%. При хорошем спросе на 1-й вариант ИС доход – 200 у.е., при слабом – 90 у.е.

Необходимо оценить у какой системы будет наибольший денежный выигрыш.

Вариант	Спрос	p	F(nk)
	Хороший	0,65
Плохой	0,35	-30
	Хороший	0,65
Плохой	0,35

K₁= 0,65*80+0,35*(-30)=41,5

K₂=0.65*70+0.35*10=49

K_опт=max k_i=k₂

Ответ: у второй системы будет наибольший денежный выигрыш.

Кроме оптимизации «в среднем» в вероятностных операциях используются и другие критерии оценки систем:

• максимум вероятности случайного события;

• максимум степени вероятностной гарантии достижения результата не ниже требуемого уровня;

• минимум среднего квадрата уклонения результата от требуемого;

• минимум дисперсии результата;

• максимум вероятностно-гарантированного результата;

• минимум среднего (байесовского) риска (минимум средних потерь).

Рассмотрение этих критериев составляет один из разделов теории принятия решений.

3.2.2. ОЦЕНКА СЛОЖНЫХ СИСТЕМ
В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

Специфические черты организационно-технических систем часто не позволяют свести операции, проводимые этими системами, к детерминированным или вероятностным. К таким чертам относятся:

1. Наличие в управляемой системе в качестве элементов (подсистем) целенаправленных индивидуумов и наличие в системе управления ЛПР, осуществляющих управление на основе субъективных моделей, что и приводит к большому разнообразию поведения системы в целом.

2. Алгоритм управления часто строит сама система управления, преследуя помимо предъявляемых старшей системой целей собственные цели, не всегда совпадающие с внешними.

3. На этапе оценки ситуации в ряде случаев исходят не из фактической ситуации, а из той модели, которой пользуется ЛПР при управлении объектом.

4. В процессе принятия решения большую роль играют логические рассуждения ЛПР, не поддающиеся формализации классическими методами математики.

5. При выборе управляющего воздействия ЛПР может оперировать нечеткими понятиями, отношениями и высказываниями.

6. В большом классе задач управления организационно-техническими системами отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта управления, а также статистика, достаточная для построения соответствующих вероятностных распределений (законов распределения исходов операций) для конкретного принятого решения.

Таким образом, несводимость операций, проводимых сложными организационно-техническими системами к детерминированным или вероятностным, не позволяет использовать для их оценки детерминистские и вероятностные критерии.

Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы, в которой обозначены:

а_i ‒ вектор управляемых параметров, определяющий свойства системы (i = 1,..., m);

n_j ‒ вектор неуправляемых параметров, определяющий состояние обстановки (j = 1,..., k);

k_ij ‒ значение эффективности системы а_i для состояния обстановки n_j;

K(a_i) ‒ эффективность системы а_i.

Каждая строка таблицы содержит значения эффективности одной системы для всех состояний обстановки n_;, а каждый столбец ‒ значения эффективности для всех систем a_i при одном и том же состоянии обстановки. В случае задания состояний обстановки одним параметром матрица эффективности может быть представлена диаграммой (рис. 2.11).

Рис. 2.11. Диаграмма эффективности систем а_i для условий n_j

В неопределенной операции могут быть известны множество состояний обстановки и эффективность систем для каждой из них, но нет данных, с какой вероятностью может появиться то или иное состояние.

В зависимости от характера неопределенности операции могут делиться на игровые и статистически неопределенные. В игровых операциях неопределенность вносит своими сознательными действиями противник. Для исследования игровых операций используется теория игр. Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. Природа рассматривается как незаинтересованная, безразличная к операции сторона (она пассивна по отношению к лицу, принимающему решение). Такие операции могут исследоваться с применением теории статистических решений.

Если операция, проводимая системой, уникальна, то для разрешения неопределенности при оценке систем используются субъективные предпочтения ЛПР. По этой причине единого критерия оценки эффективности для неопределенных операций не существует. Разработаны лишь общие требования к критериям и процедурам оценки и выбора оптимальных систем. Основными требованиями являются:

· оптимальное решение не должно меняться с перестановкой строк и столбцов матрицы эффективности;

· оптимальное решение не должно меняться при добавлении тождественной строки или тождественного столбца к матрице эффективности;

· оптимальное решение не должно меняться от добавления постоянного числа к значению каждого элемента матрицы эффективности;

· оптимальное решение не должно становиться неоптимальным, а неоптимальное оптимальным в случае добавления новых систем, среди которых нет ни одной более эффективной системы;

· если системы a_i и a_j оптимальны, то вероятностная смесь этих систем тоже должна быть оптимальна.

В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:

• среднего выигрыша;

• Лапласа;

• осторожного наблюдателя (Вальда);

• максимакса;

• пессимизма-оптимизма (Гурвица);

• минимального риска (Сэвиджа).

Рассмотрим эти критерии на примере.

Пример 2.2. Необходимо оценить один из трех разрабатываемых программных продуктов a_i для борьбы с одним из четырех типов программных воздействий K_j. Матрица эффективности представлена в табл. 2.11.

Таблица 2.11. Матрица эффективности программных продуктов

ai	kj
k1	k2	k3	k4
a1	0,1	0,5	0,1	0,2
a2	0,2	0,3	0,2	0,4
a3	0,1	0,4	0,4	0,3

Здесь a_i ‒ i-й программный продукт, i = {1, 2, 3};

k_j ‒ оценка эффективности применения i-го программного продукта при j-м программном воздействии {j} 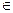t = {1, 2, 3, 4}.

Критерий среднего выигрыша. Данный критерий предполагает задание вероятностей состояний обстановки р_i Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям обстановки:

Оптимальной системе будет соответствовать эффективность

Если в данном примере задаться вероятностями применения
противником программных воздействий р₁ = 0,4, р₂ = 0,2, p₃ = 0,1 и р₄ = 0,3, то получим следующие оценки систем:

К(а₁) = 0,4•0,1 + 0,2 • 0,5 + 0,1 • 0,1 + 0,3 • 0,2 = 0,21;

К(а₂) = 0,4 • 0,2 + 0,2 • 0,3 + 0,1 • 0,2 + 0,3 • 0,4 = 0,28;

К(а₃) = 0,4 • 0,1 + 0,2 • 0,4 + 0,1 • 0,4 + 0,3 • 0,3 = 0,25.

Оптимальное решение ‒ система а₂.

Для применения критерия среднего выигрыша необходим, по существу, перевод операции из неопределенной в вероятностную, причем произвольным образом.

Критерий Лапласа. В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными. Исходя из этого

Рассчитаем эффективность систем по данному критерию для приведенного примера:

К(а₁) = 0,25 (0,1 + 0,5 + 0,1 + 0,2) = 0,225;

К(а₂) = 0,25 (0,2 + 0,3 + 0,2 + 0,4) = 0,275;

К(а₃) = 0,25 (0,1 + 0,4 + 0,4 + 0,3) = 0,3.

Оптимальное решение ‒ система а₃ Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

Критерий осторожного наблюдателя (Вальда). Это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях. Критерий основывается на том, что, если состояние обстановки неизвестно, нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы.

В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям обстановки

Оптимальной считается система из строки с максимальным значением эффективности:

Применение критерия максимина к нашему примеру дает следующие оценки:

K(a₁) = min(0,l; 0,5; 0,1; 0,2) = 0,1;

К(а₂) = min(0,2; 0,3; 0,2; 0,4) = 0,2;

К(а₃) = min(0,l; 0,4; 0,4; 0,3) = 0,1.

Оптимальное решение ‒ система а₂.

Максиминный критерий ориентирует на решение, не содержащее элементов риска: при любом из возможных состояний обстановки выбранная система покажет результат операции не хуже найденного максимина. Такая осторожность является в ряде случаев недостатком критерия. Другой недостаток - он не удовлетворяет требованию 3 (добавление постоянного числа к каждому элементу столбца матрицы эффективности влияет на выбор системы).

Критерий максимакса. Этим критерием предписывается оценивать системы по максимальному значению эффективности и выбирать в качестве оптимального решения систему, обладающую эффективностью с наибольшим из максимумов:

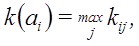
Оценки систем на основе максимаксного критерия в нашем примере принимают такие значения:

K(a₁) = max (0,1; 0,5; 0,1; 0,2) = 0,5;

К(а₂) = max (0,2; 0,3; 0,2; 0,4) = 0,4;

К(а₃) = max (0,1; 0,4; 0,4; 0,3) = 0,4.

Оптимальное решение ‒ система а₁. Критерий максимакса ‒ самый оптимистический критерий. Те, кто предпочитает им пользоваться, всегда надеются на лучшее состояние обстановки и, естественно, в большой степени рискуют.

Критерий пессимизма-оптимизма (Гурвица). Это критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует, учитывая самое высокое и самое низкое значения эффективности, занимать промежуточную позицию (взвешиваются наихудшие и наилучшие условия). Для этого вводится коэффициент оптимизма а(альфа) (0 < а < 1), характеризующий отношение к риску лица, принимающего решение. Эффективность систем находится как взвешенная с помощью коэффициента а (альфа) сумма максимальной и минимальной оценок:

K(a_t) = а max + (1 - a) min k_u.

j j j j

Условие оптимальности записывается в виде

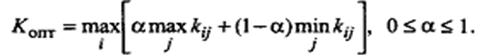
Зададимся значением а = 0,6 и рассчитаем эффективность систем для рассматриваемого примера:

К(а₁) = 0,6 • 0,5+(1-0,6) • 0,1 = 0,34;

К(а₂) = 0,6 • 0,4+(1-0,6) • 0,2 = 0,32;

К(а₃) = 0,6 • 0,4+(1-0,6) • 0,1 = 0,28.

Оптимальной системой будет а₁.

При а(альфа) = 0 критерий Гурвица сводится к критерию максимина, при а = 1 ‒ к критерию максимакса. Значение а может определяться методом экспертных оценок. Очевидно, что, чем опаснее оцениваемая ситуация, тем ближе величина а(альфа) должна быть к единице, когда гарантируется наибольший из минимальных выигрышей или наименьший из максимальных рисков.

На практике пользуются значениями коэффициента а(альфа) в пределах 0,3-0,7. В критерии Гурвица не выполняются требования 4 и 5.

Критерий минимального риска (Сэвиджа). Минимизирует потери эффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце:

После преобразования матрицы используется критерий минимакса:

K(a_i)= max ∆ кij…j

К_опт = min(max ∆ к_ij).i j

Таблица 2.12

ai	kj
k1	k2	k3	k4
a1	0,1		0,3	0,2
a2		0,2	0,2
a3	0,1	0,1		0,1

Оценим эффективность систем из приведенного примера в соответствии с данным Матрица потерь критерием. Матрице эффективности (см. табл. 2.11) будет соответствовать матрица потерь (табл. 2.12). Тогда

К(а₁) = max(0,l; 0; 0,3; 0,2) = 0,3;

К(а₂) = max(0; 0,2; 0,2; 0) = 0,2;

К(а₃) = max(0,1; 0,1; 0; 0,1) = 0,1.

Оптимальное решение система а₃. О критерии Сэвиджа можно сказать, что он, как и критерий Вальда, относится к числу осторожных критериев. По сравнению с критерием Вальда в нем придается несколько большее значение выигрышу, чем проигрышу. Основной недостаток критерия – не выполняется требование 4.

Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

– природа конкретной операции и ее цель (в одних операциях допустим риск, в других - нужен гарантированный результат);

– причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

– характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Выбор какого-то одного критерия приводит к принятию решения по оценке систем, которое может быть совершенно отличным от решений, диктуемых другими критериями. Это наглядно подтверждают результаты оценки эффективности систем применительно к примеру 2.2 по рассмотренным критериям (табл. 2.13).

Таблица 2.13 Сравнительные результаты оценки систем

	ki	K(ai ) по критериям
ai	k1	k2	kз	k4	среднего выиг-рыша	Лап- ласа	Вальда	макси-макса	Гур-вица	Сэвиджа
a1	0,1	0,5	0,1	0,2	0,21	0,225	0,1	0,5	0,34	0,3
a2	0,2	0,3	0,2	0,4	0,28	0,275	0,2	0,4	0,32	0,2
a3	0,1	0,4	0,4	0,3	0,25	0,300	0,1	0,4	0,28	0,1

Тип критерия для выбора рационального варианта должен быть оговорен на этапе анализа систем, согласован с заказывающей организацией и в последующих задачах синтеза информационных и других сложных систем предполагается заданным. Процесс выбора вида критерия для учета неопределенности достаточно сложен. Устойчивость выбранного рационального варианта можно оценить на основе анализа по нескольким критериям. Если существует совпадение, то имеется большая уверенность в правильности выбора варианта решения.

В случаях, когда системы, выбранные по различным критериям, конкурируют между собой за право быть окончательно выбранными, могут применяться процедуры, основанные на мажоритарной обработке результатов оценки по простому большинству голосов. Особенностью мажоритарной обработки является опасность выбора системы, не являющейся лучшей.

В любом случае при выделении множества предпочтительных систем по разным критериям окончательный выбор системы должен осуществляться ЛПР.

4. КОЛИЧЕСТВЕННЫЕ МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ

Системный подход к явлениям – одно из важнейших интеллектуальных свойств человека.

(В.Н. Спецнадель, профессор)

4.1. Метод SMART

Существуют эвристические методы, не имеющие строгого математического обоснования, но использующие простые процедуры получения информации и её агрегации в общую оценку альтернативы.

Одним из наиболее известных методов такого типа является метод SMART, предложенный В. Эдвардсом. Метод можно представить как совокупность следующих этапов:

1. Упорядочить критерии по важности.

2. Присвоить наиболее важному критерию оценку 100 баллов. Исходя из попарного отношения критериев по важности, дать в баллах оценку каждому из критериев.

3. Сложить полученные баллы. Произвести нормировку весов критериев, разделив присвоенные баллы на сумму весов.

4. Измерить значение каждой альтернативы по каждому из критериев по шкале от 0 до 100 баллов.

5. Определить общую оценку каждой альтернативы, используя формулу взвешенной суммы баллов.

6. Выбрать как лучшую альтернативу, имеющую наибольшую общую оценку.

7. Оценить чувствительности результата к изменениям весов.

По признанию автора, метод SMART не учитывает возможную зависимость измерений и неаддитивность при определении общей ценности альтернативы.

Однако, по его мнению, метод прост и надёжен при практических применениях, что более существенно. Проверка чувствительности к изменениям весов позволяет учесть влияние неточностей при измерениях и возможной зависимости между критериями.

Дата добавления: 2014-12-27