Основные уравнения, характеризующие состояние провода в пролете

Пусть на провод действует только вертикальная, равномерно распределенная по длине нагрузка, например, нагрузка от собст­венного веса провода. Под действием нагрузки провод провис­нет, подобно гибкой нити (рисунок 4.1). Идеальная гибкая нить, не обладающая жесткостью на изгиб, при такой загрузке принимает очертание цепной линии. Кривая провисания провода за счет наличия некоторой жесткости лишь приближается по форме к цепной линии. При этом напряжение в проводе будет обуслов­лено не только растяжением, но отчасти и изгибом. Однако на­пряжение в проводе из-за изгиба обычно не превышает 0,01 на­пряжения от растяжения. Поэтому можно считать, что напряже­ние в проводе возникает только за счет растягивающего усилия, направленного в каждой точке по касательной к кривой прови­сания. Оно определяется по формуле:

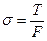, (4.1)

где Т - тяжение по проводу сечением F.

Уравнение стрелы провеса провода в пролете:

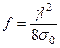, (4.2)

где l - длина пролета линии; 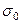- напряжение в материале провода в низшей точке 0.

Уравнение состояния провода в пролете:

, (4.3)

где - удельная нагрузка от веса провода; 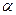- температурный коэффициент линейного расширения; - коэффициент упругого удлинения (, Е – модуль упругости); и – соответственно нагрузка и напряжение при определенной температуре .

Если обозначить:

и , то получим кубическое уравнение состояния провода:

, (4.4)

откуда с погрешностью решения не более 5 % получаем формулу:

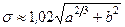. (4.5)

Дата добавления: 2014-12-27