Послідовність розрахунків похибок за непрямих вимірювань

Приклад розрахунку похибок за прямих вимірювань

Виміряти довжину нитки математичного маятника. Вимірювання проводимо 5 разів лінійкою. При цьому отримуємо результати: 50,2; 60,4; 59,9; 60,0; 60,3 см.

1. Заходимо середнє арифметичне значення довжини маятника:

.

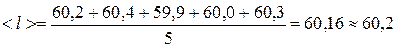2. Визначаємо

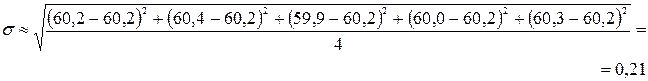3. Знаходимо величину 3σ=0,63 та порівнюємо її з 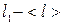. Всі значення 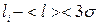, тому залишаємо всі результати. Промахів нема.

4. Визначаємо

.

5. Знаходимо 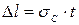при надійності 0,99. Коефіцієнт Стьюдента за таблицею при надійності 0,99 і кількості вимірювань 5 дорівнює , тоді .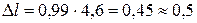

6. Знаходимо відносну похибку

.

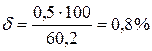7. Записуємо кінцевий результат у вигляді

, .

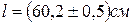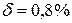У випадку прямих вимірювань похибки вимірювань знаходять порівняно просто. Проте в більшості випадків шукана величина є функцією декількох вимірюваних величин 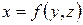. Помилки вимірювань, як правило, досить малі порівняно з вимірюваними величинами, тому для обчислення похибок непрямих вимірювань можна скористатися диференційним обчисленням.

Порядок визначення похибки у випадку непрямих вимірювань такий:

1. Взяти натуральний логарифм від обох частин формули.

2. Знайти диференціал отриманих виразів за всіма аргументами функції.

3. Замінити диференціали у цьому виразі похибками вимірювань Δy, Δz.

4. Похибки Δy, Δz кожної величини визначити за правилами, які вказані для прямих вимірювань.

5. Змінити “мінуси”, що з’явилися при логарифмуванні та диференціюванні, на “плюси”, тому що похибки окремих величин необхідно скласти.

6. З відносної похибки обчислити надійний інтервал шуканої величини 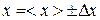, де .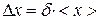

7. Записати кінцевий результат у вигляді

, .

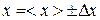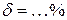Дата добавления: 2014-12-27