Теоретичні відомості. Вимірювання маси тіла

РУХ ТІЛ ПО ПОХИЛІЙ ПЛОЩИНІ

Вимірювання маси тіла

Контрольні запитання і завдання

1. Які вимірювання називають прямими?

2. Які вимірювання називають непрямими?

3. Які помилки вимірювань відносять до систематичних, випадкових та промахів?

4. Що називають абсолютною похибкою вимірювань?

5. Що називають відносною похибкою вимірювань?

6. Що таке надійний інтервал?

7. Наведіть порядок розрахунку похибок у разі прямих вимірювань.

8. Наведіть порядок розрахунку похибок у разі непрямих вимірювань.

9. Визначте відносну та абсолютну похибки вимірювань маси тіла за табл.2.2. (варіант та надійність Р вказує викладач).

10. Отримайте розрахункову формулу до визначення відносної похибки у випадку непрямих вимірювань (за вказівкою викладача).

Таблиця 2.2

№	Маса тіла, г
Варіант1	Варіант2	Варіант3	Варіант4	Варіант5	Варіант6
1.	10,55	20,54	30,96	40,21	50,42	60,15
2.	10,51	20,65	30,95	40,25	50,43	60,11
3.	10,58	20,83	30,98	40,24	50,40	60,13
4.	10,53	20,86	30,99	40,70	50,46	60,17
5.	10,59	20,57	30,97	40,28	50,44	60,16

Лабораторна робота № 1-03

Мета роботи:

1. Вивчення особливостей поступального рівноприскореного руху з урахуванням тертя ковзання під час ковзання тіла з похилої площини з тертям.

2. Вивчення характеристик прискореного обертального руху; визначення коефіцієнта тертя ковзання.

Тертя – це механічний опір, що виникає під час відносного переміщення двох стичних тіл у площині дотику (тіла взагалі можуть бути твердими, рідкими і газоподібними). Тертя – це складний дисипативний необоротний процес, який супроводжується виділенням тепла, електризацією тіл, їх руйнуванням тощо. Сила опору F, яка напрямлена протилежно відносному переміщенню тіл, називається силою тертя.

Тертя називають зовнішнім при виникненні сили тертя між поверхнями двох різних тіл, що стикаються і внутрішнім, якщо сили тертя виникають між шарами рідини або газу. Зовнішнє тертя звичайно розділяють на тертя ковзання та тертя кочення. Якщо складова сили, прикладена до тіла паралельна площі стичних поверхонь, недостатня для виникнення ковзання, силу тертя називають неповною. Неповна сила тертя змінюється від нуля до деякого максимального значення 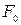, що називається силою тертя спокою. При подальшому збільшенні сили, прикладеної до тіла, починається ковзання. Кулон експериментально встановив, що сила тертя ковзання не залежить від площі стичних поверхонь і пропорційна силі нормального тиску (реакції опори).

Відношення граничної сили тертя 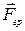до нормального тиску (притискуючої сили) називається статичним коефіцієнтом тертя (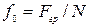). Сила тертя відхиляє повну реакцію 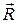від нормалі на кут 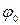− кут тертя спокою (рис. 3.1а). Тангенс кута тертя спокою дорівнює статичному коефіцієнту тертя

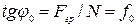, (3.1)

де − зовнішня рушійна сила.

Відношення сили тертя під час руху до сили нормального тиску називається динамічним коефіцієнтом тертя ковзання. Він дещо менший від статичного коефіцієнта тертя ковзання.

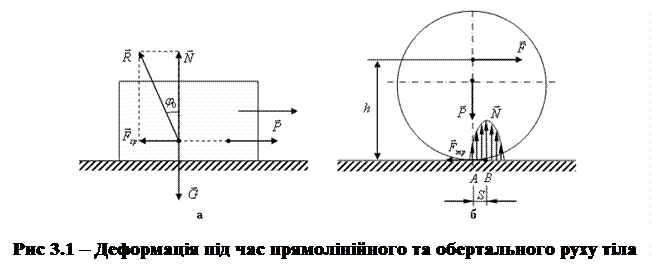При коченні криволінійних поверхонь виникає опір, який називають тертям кочення. Воно залежить від пружних властивостей матеріалів, кривизни поверхонь стичних тіл і сили нормального тиску. При русі циліндра по площині в зоні їхнього контакту (рис. 3.1б) внаслідок деформації площини (деформацією циліндра нехтуємо; це спрощення мало впливає на результат аналізу) створюються пружні деформації, які розподілені нерівномірно (деформація площини кочення несиметрична).

Позаду циліндра деформація площини не зникає або зникає через деякий час. Це призводить до того, що рівнодійна елементарних сил реакції площини N є похилою до поверхні кочення і не проходить через вісь циліндра. Вона також зміщена відносно вісі циліндра, який котиться, на величину s=АВ в бік руху тіла. Відстань s називається коефіцієнтом тертя кочення. Для кочення тіла потрібно подолати момент пари сил:

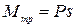, (3.2)

де Р − сила, яка притискує тіло до опорної поверхні.

Якщо до циліндра паралельно опорній площині на відстані h прикладена рушійна сила F, то в зоні контакту виникає сила тертя 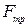. Під час рівномірного кочення моменти рушійної сили і опору дорівнюють один одному:

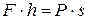, (3.3)

звідки

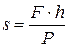. (3.4)

На основі даної формули дослідним шляхом визначається коефіцієнт тертя кочення s.

Для визначення коефіцієнта тертя ковзання використовують горизонтальну або похилу площини. У найпростішому випадку установка для визначення f ₀ представляє собою стальну площину 1, виставлену установочними гвинтами за рівнем строго горизонтально (рис. 3.2).

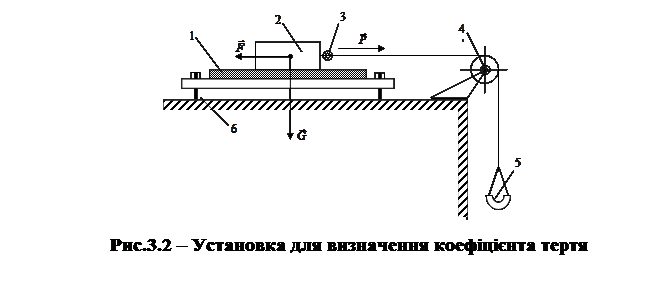По площині переміщується брусок 2(один з пари досліджуваних матеріалів); рекомендується визначити коефіцієнти f ₀ для сталі по сталі, чавуну по сталі, пластмаси по сталі і т. д. До бруска гачком 3 кріпиться один кінець шнура, перекинутого через спрямовуючий блок 4(блок встановлюють паралельно площині 1). До другого кінця шнура прикріплено шальку 5. Шалька поступово навантажується дрібними гирями або дротом доки досліджуваний зразок матеріалу не почне рівномірно рухатись по площині.

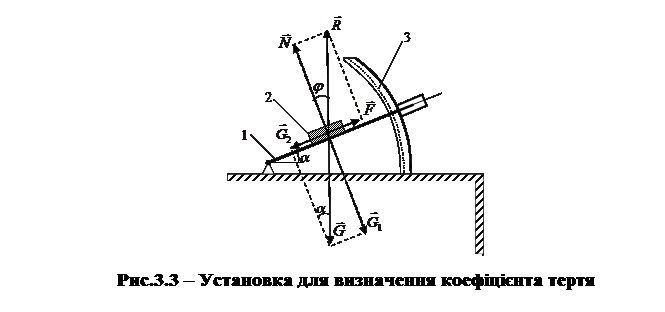
Коефіцієнт тертя ковзання f вимірюється також на похилій площині. Похила площина 1 за допомогою гвинтового механізму 4 може бути встановлена під різними кутами 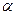до горизонтальної площини (рис. 3.3). Величина кута нахилу фіксується по шкалі 3. За збільшення кута 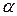зростає складова сили тяжіння G i також сила тертя спокою F. При 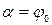маємо 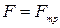і зразок 2 почне рухатись. Очевидно, що

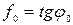. (3.5)

Платформа обертається навколо осі 1 в одну сторону на кут до 45°.

Кут нахилу відлічується по шкалі 3. Час, за який зразок пройде відстань l:

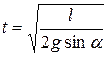. (3.6)

Це реалізується за умови 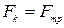. Коефіцієнт тертя ковзання .

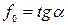Кінематичний коефіцієнт тертя ковзання за рівноприскореного руху визначається за формулою:

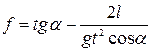(3.7)

Чисте кочення циліндра (котка) по похилій площині без ковзання реалізується за умови

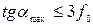, (3.8)

де 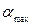− найбільший кут нахилу площини, за якого відбувається чисте кочення циліндра.

Коефіцієнт тертя кочення обчислюється за формулою:

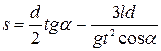(3.9)

де d − діаметр котка; 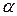− кут нахилу площини до горизонту; 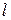− відстань, яку проходить коток за час t ().

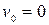Дата добавления: 2014-12-27