Из учебного пособия

Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учебное пособие М.: Вузовский учебник, 2007, 2008, 2012. - Стр. 134-156

2.5. Двойственные задачи линейного программирования[1]

В 1975 г. наш соотечественник Л.В. Канторович(1912-1986) был удостоен Нобелевской премии по экономике (совместно с американским экономистом Т. Купмансом) за разработку теории оптимального использования ресурсов.

Достижением Л.В. Канторовича является введение в математическую и экономическую науки понятия "линейное программирование" (1939). Основная заслуга Л.В.Канторовича заключается в разработке единого подхода к широкому кругу экономических задач о наилучшем использовании ресурсов на базе линейного программирования. Им были введены "двойственные оценки" ресурсов (сам Л.В.Канторович называл их объективно обусловленными оценками), показывающие степень ценности этих ресурсов для общества. Двойственные оценки получили разнообразное истолкование в зависимости от рассматриваемого круга задач в работах самого Л.В.Канторовича, его последователей в СССР и западных ученых. Если в западной литературе наиболее популярны так называемые "теневые цены" на ресурсы, то Л.В.Канторовича более интересовала основанная на двойственных оценках теория дифференциальной ренты.

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к исходной задаче линейного программирования, состоящей в нахождении максимального значения функции

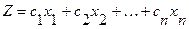(2.5.1)

при ограничениях

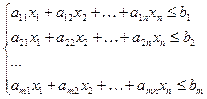(2.5.2) . (2.5.3)

Задача, состоящая в нахождении минимального значения функции

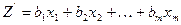(2.5.4)

при ограничениях

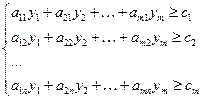, (2.5.5)

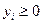
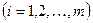, (2.5.6)

называется двойственной по отношению к задаче (2.5.1) – (2.5.3).

Переменные двойственной задачи y_i в экономической литературе получили различные названия: учетные, неявные, теневые, объективно обусловленные оценки, или двойственные оценки, или «цены» ресурсов.

Рассмотренная пара взаимно двойственных задач может быть экономически интерпретирована, например, так.

Прямая задача: сколько и какой продукции 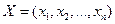надо произвести, чтобы при заданных стоимостях единицы продукции с_j (j= 1, n), объемах имеющихся ресурсов b_i, (i = 1, m) и нормах расходов a_ij максимизировать выпуск продукции в стоимостном выражении.

Двойственная задача: какова должна быть оценка единицы каждого из ресурсов 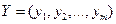, чтобы при заданных b_i, с_j, и a_ij минимизировать общую оценку затрат на всю продукцию.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой задачи

Задачи (2.5.1) – (2.5.3) и (2.5.4) – (2.5.6) образуют пару задач, называемую в линейном программировании двойственной парой.

Двойственная задача по отношению к исходной задаче составляется согласно следующим правилам:

1) если целевая функция исходной задачи формулируется на максимум, то целевая функция двойственной задачи – на минимум (и, наоборот), при этом в двойственной задаче на максимум все неравенства в функциональных ограничениях имеют вид (£), в задаче на минимум — вид (³);

2) матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи и аналогичная матрица А ^T в двойственной задаче получаются друг из друга транспонированием;

3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной;

4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной;

5) каждому ограничению одной задачи соответствует переменная другой задачи, номер переменной совпадает с номером ограничения. При этом ограничению, записанному в виде неравенства £, соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной; задачи может принимать как положительные, так и отрицательные значения.

Многие задачи линейного программирования первоначально составляются в виде исходных или двойственных задач, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.

Дата добавления: 2014-12-27