Модели двойственных задач

Различают несимметричные и симметричные двойственные задачи. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем в двойственной задаче переменные могут быть и отрицательными. В симметричных задачах система ограничений, как исходной задачи, так и двойственной задачи задается неравенствами, причем на двойственные переменные налагается условие неотрицательности.

Пример 2.5.1. Сформулировать модель задачи, двойственной к «задаче о костюмах».

Исходная задача Двойственная задача

Переменные: Переменные:

х ₁ – число женских костюмов; y₁ – двойственная оценка ресурса шерсть;

x ₂ – число мужских костюмов. y₂ - двойственная оценка ресурса лавсан;

Максимизировать целевую функцию y₃ - двойственная оценка ресурса труд;

f (x) = 10 х ₁ + 20 х ₂y₄ - двойственная оценка к ограничению по

мужским костюмам.

Ограничения задачи имеют вид: Минимизировать целевую функцию

х ₁ + 3, 5 х ₂£350,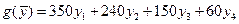

2 х ₁ + 0, 5 х ₂£240, Ограничения задачи имеют вид:

х ₁ + х ₂£150,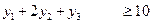

х ₂³60,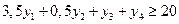

х ₁³0.

При решении ЗЛП с помощью симплексных таблиц решение двойственной задачи содержится в последней строке последней симплексной таблицы (это 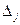). При чем основные переменные двойственной задачи содержатся в столбцах, соответствующих дополнительным переменным исходной задачи, а дополнительные переменные двойственной задачи содержатся в столбцах, соответствующих основным (первоначальным) переменным исходной задачи (табл. 2.5.1 ).

Табл. 2.5.1.

Переменные исходной задачи
Первоначальные	Дополнительные
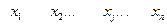
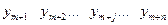
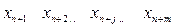
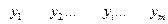
Дополнительные	Первоначальные
Переменные двойственной задачи

В табл. 2.5.3 приведено решение «задачи о костюмах». Из пятой строки третьей симплекс-таблицы можно выписать ответ двойственной задачи.

Основные переменные:

y₁ - двойственная оценка ресурса шерсть = 4

y₂ - двойственная оценка ресурса лавсан = 0

y₃ – двойственная оценка ресурса труд = 6

y₄ - двойственная оценка мужских костюмов = 0.

Дополнительные переменные:

y₅ = 0

y₆ = 0

Значение целевой функции:

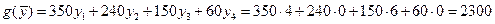
Установим следующее соответствие между переменными исходной задачи о костюмах и переменными двойственной задачи (Табл. 2.51.):

Табл. 2.5.1.

Переменные исходной задачи
Первоначальные	Дополнительные
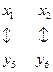
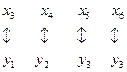
Дополнительные	Первоначальные
Переменные двойственной задачи

Табл. 2.5.3. Решение задачи о костюмах симплексным методом

№	Базис	Ci	Cj План							-М
A1	A2	A3	A4	A5	A6	P	Q
	A3				3.5
A4				0.5
A5
P	-М							-1
				-10	-М-20				М
	A3								3.5
	A4								0.5
	A5
	A2								-1
				-10
	A3							-1	2.5
	A4							-2	-1.5
	A1
	A2								-1
									-10
	A6					0.4		-0.4
	A4					0.6		-2.6
	A1					-0.4		1.4
	A2					0.4		-0.4

При решении ЗЛП с помощью надстройки EXCEL Поиск решения решение двойственной задачи содержатся в отчете Устойчивость. При чем основные переменные двойственной задачи содержатся в столбце «Теневая цена», а дополнительные переменные двойственной задачи содержатся в столбце, «Нормируемая стоимость».

Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
	$A$2	x1					4,285714286
	$B$2	x2
Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
	$C$4
	$C$5					1E+30
	$C$6					23,07692308
	$C$7						1E+30

Рис. 2.5.1. Содержимое отчета Устойчивость задачи о костюмах.

Если в одной из взаимно двойственных задач на­рушается единственность оптимального решения, то опти­мальное решение двойственной задачи вырожденное (см. пример 2.3.5., табл. 2.3.5-2.3.6).

Основные утверждения о взаимно двойственных задачах содержатся в следующих теоремах.

Теорема. Первая теорема двойственности. Для взаимно двойственных задач имеет место один из взаимоисключающих случаев.

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:

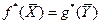. (2.5.7)

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Экономический смысл первой (основной) теоремы двойственнос­ти. План производства 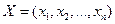и набор цен (оценок) ресурсов 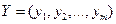оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от продукции, найден­ная при "внешних" (известных заранее) ценах 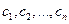равна затратам на ресурсы по "внутренним" (определяемым только из решения задачи) ценам 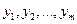. Для всех же других планов X и Y обеих задач прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы .

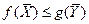Экономическое содержание первой теоремы двойственности состоит также и в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определенных оценок ресурсов. Причем цена продукта, полученного в результате реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадения значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными.

Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей оценки продукции и ресурсов обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставлять и балансировать затраты и результаты системы.

Теорема. Вторая теорема двойственности (теорема о дополняющей нежесткости). Пусть 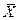=(x₁, x₂,..., x_n) – допустимое решение прямой задачи, а 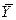= (y₁, y₂,..., y_m) – допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответственно прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

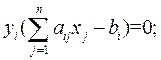(2.5.8)

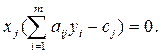(2.5.9)

Условия (2.5.8) и (2.5.9) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений (неравенств) прямой задачи на величину

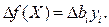(2.5.10)

Решая ЗЛП симплекс-методом, мы одновременно решаем и исходную и двойственную задачи.

Дата добавления: 2014-12-27