Анализ полученных оптимальных решений

Рассмотрим экономическую интерпретацию двойственной задачи на примере задачи о коврах.

Пример 2.5.2. Используя постановку задачи о коврах, выполнить следующие задания.

1. Сформулировать экономико-математическую модель задачи о коврах на максимум общей стоимости продукции, используя данные табл. 2.3.1.

2. Используя Поиск решения, найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальной.

3. Сформулировать экономико-математическую модель двойственной задачи к задаче о коврах.

4. Найти оптимальный план двойственной задачи, используя теоремы двойственности, пояснить равенство нулю x ₁ и x ₄.

5. Используя протоколы Поиска решения, выполнить анализ полученного оптимального решения исходной задачи.

6. Сравнить результаты решения задачи, полученные вручную с помощью симплексных таблиц и полученные в Поиске решения.

7. Определить, как изменится общая стоимость и план выпуска продукции при увеличении запаса ресурса труд на 12 ед.

Решение

1. Сформулируем экономико-математическую модель задачи. Обозначим через Х ₁, Х ₂, Х ₃, Х ₄ число ковров каждого типа. Целевая функция имеет вид:

f (x) = 3 Х ₁ + 4 Х ₂ + 3 Х ₃ +Х _{4 ,}

а ограничения по ресурсам:

7 Х ₁ + 2 Х ₂ + 2 Х ₃ + 6 Х ₄ 80,

5 Х ₁ + 8 Х ₂ + 4 Х ₃ + 3 Х ₄ 480,

2 Х ₁ + 4 Х ₂ +Х ₃ + 8 Х ₄ 130,

Х ₁, Х ₂, Х ₃, Х ₄ 0.

2. Поиск оптимального плана выпуска. Решение задачи выполним с помощью надстройки Excel Поиск решения. Технология решения задачи была подробно рассмотрена в задаче о костюмах. В нашей задаче оптимальные значения вектора Х = (Х ₁, Х ₂, Х₃, Х ₄)будут помещены в ячейках В3:Е3, оптимальное значение целевой функции в ячейке F4.

Введем исходные данные. Сначала опишем целевую функцию с помощью функции СУММПРОИЗВ (рис. 2.5.2).

А потом введем данные для левых частей ограничений. В Поиске решениявведем направление целевой функции, адреса искомых переменных, добавим ограничения. На экране появится диалоговое окно Поискрешения с введенными условиями (рис. 2.5.3.).

После ввода параметров для решения ЗЛП следует нажать кнопку Выполнить. На экране появится сообщение, что, решение найдено (рис. 2.5.4.).

.

Рис. 2.5.2. Вводится функция для вычисления значения целевой функции

Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг пряжи (ресурс сырье) будет использовано 280 кг.

Рис. 2.5.3. Введены все условия задачи.

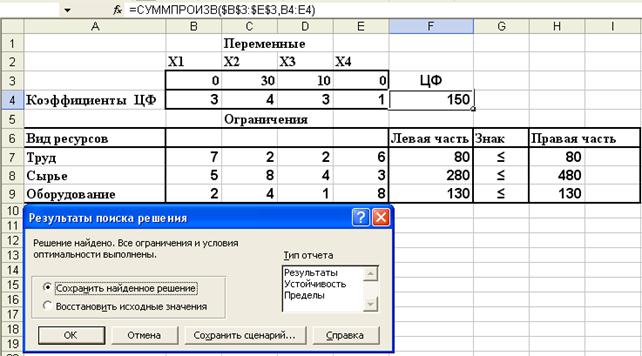
Рис. 2.5.4. Решение найдено

Создание отчета по результатам поиска решения. Excel позволяет представить результаты поиска решения в форме отчета (табл. 2.5.4). Существует три типа таких отчетов:

– Результаты(Answer). В отчет включаются исходные и конечные значения целевой и изменяемых ячеек, дополнительные сведения об ограничениях.

– Устойчивость(Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.

– Пределы(Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек, в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

Таблица 2.5.4. Содержание отчета по результатам

Отчет по результатам
Целевая ячейка (максимум)
	Ячейка	Имя	Исходно	Результат
	$F$4	коэф. в ЦФ
Изменяемые ячейки
	Ячейка	Имя	Исходно	Результат
	$B$3	значение Х1
	$C$3	значение Х2
	$D$3	значение Х3
	$E$3	значение Х4
Ограничения
	Ячейка	Имя	Значение	Формула
	$F$7	труд левая часть		$F$7<=$H$7
	$F$8	сырье левая часть		$F$8<=$H$8
	$F$9	оборудование левая часть		$F$9<=$H$9

В отчете по результатам содержатся оптимальные значения переменных Х ₁, Х ₂, Х ₃, Х ₄, которые соответственно равны 0; 30; 10; 0; значение целевой функции – 150, а также левые части ограничений.

Содержание остальных отчетов будет рассмотрено ниже.

Дата добавления: 2014-12-27