Вычисление вероятности заданного отклонения нормальной случайной величины

Вероятность попадания в заданный интервал нормальной случайной величины

Если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее заданному интервалу, вычисляется по формуле (5.9а). Подставив в формулу (5.9а) значение плотности распределения из (5.16) для нормального распределения N(a, s) и сделав ряд преобразований, вероятность того, что Х примет значение, принадлежащее заданному интервалу [x₁, x₂], будет равна:

,

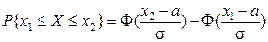(5.18)

где а – математическое ожидание.

Пример 7. Случайная величина Х распределена по нормальному закону. Математическое ожидание a=60, среднеквадратическое отклонение s=20. Найти вероятность попадания случайной величины Х в заданный интервал (30;90).

Решение. Искомая вероятность вычисляется по формуле (5.18).

Получим: P(30 < X < 90) = Ф((90 – 60) / 20) –Ф((30 – 60)/20) = 2Ф(1,5).

По таблице Приложения 1: Ф(1,5) = 0,4332.

P(30 < X < 90)=2 Ф(1,5) = 2×0,4332 = 0,8664.

Вероятность попадания случайной величины Х в заданный интервал (30; 90) равна: P(30<X<90) =2 Ф(1,5) =2×0,4332= 0,8664.

Задачи вычисления вероятности отклонения нормальной случайной величины от заданного значения связаны с различного рода ошибками (измерения, взвешивания). Ошибки разного рода обозначаются переменной e.

Пусть e – отклонение нормально распределённой случайной величины Х по модулю. Требуется найти вероятность того, что отклонение случайной величины Х от математического ожидания не превысит заданного значения e. Данная вероятность записывается в виде: P(|X-a|) ≤ e.

Предполагается, что в формуле (5.18) отрезок [х₁; х₂] симметричен относительно математического ожидания –а. Таким образом: a–х₁=e; х₂ –a =e. Отсюда можно выразить границы отрезка [х₁; х₂], которые будут иметь вид:

х1=а –e; х2=а + e.

(5.19)

В правую часть (5.18) подставляются значения х₁, х₂ из (5.19). Далее выражение в фигурных скобках левой части формулы (5.18) переписывается в виде двух неравенств:

1) х₁ ≤ X и заменяется в нём х₁ согласно (5.19), получится:

а–e ≤ X или а–X ≤ e.

2) X ≤ х₂, аналогично заменяется х₂ из (5.19), получится:

X ≤ а+e или X–a ≤ e.

В результате этих замен формулу (5.18) можно переписать в виде:

P (|X–a| ≤ e) = 2Ф(e/s) = 2Ф(t),

(5.20)

где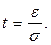

Через функцию Лапласа выражается и функция нормального распределения в общем случае N(a, s):

.

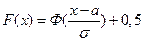(5.21)

Далее рассматриваются несколько примеров вычисления вероятности отклонения нормально распределённой случайной величины от своего математического ожидания.

Пример 8.

Производится измерение диаметра детали. Случайные ошибки измерения принимаются за случайную величину Х и подчинены нормальному закону с математическим ожиданием а=0, со средним квадратическоим отклонение s=1мм. Найти вероятность того, что измерение будет сделано с ошибкой, не превышающей по абсолютной величине 2мм.

Решение.

Дано: e=2, s=1мм, а=0.

По формуле (5.20): P (|X–0| ≤ 2) = 2Ф(e/s) = 2Ф(2/1) = 2Ф(2,0).

По таблице Приложения 1 можно найти: Ф (2,0)=0,4772.

Вероятность того, что измерение будет сделано с ошибкой, не превышающей по абсолютной величине 1 мм равна:

P (|X| ≤ e) = 2×0,4772 = 0,9544.

Пример 9.

Случайная величина, распределенная по нормальному закону с параметрами: а=50 и s=15.

Найти вероятность того, что отклонение случайной величины от своего математического ожидания – а будет меньше 5.

Решение.

По формуле (5.20) вычисляем вероятность отклонения случайной величины:

P(|X– 50| < 5) = 2Ф(5/15) = 2Ф(0,333) = 2×0,1293 = 0,2586.

Вероятность того, что отклонеиие случайной величина от своего математического ожидания будет меньше пяти, равна: P(|X–a|<5)=0,2586.

Пример 10.

Имеется случайная величина, распределенная по нормальному закону с параметрами а и s. Найти вероятность того, что случайная величина отклонится от своего математического ожидания – а не больше, чем на 3s.

Решение.

По условию задачи e ≤ 3s. С учетом (5.20) будем иметь:

,

где Ф(3) вычисляется по таблице функции Лапласа (Приложение 1):

Ф(3)» 0.49865.

В итоге: P(|X-a| £ 3s) = 2Ф(3)» 0,9973.

5.4. Вопросы для самоконтроля по теме «Случайная величина»

1. Дискретная случайная величина X имеет закон распределения вероятностей:

X	-1
P	0,3	0,7

Тогда математическое ожидание M(X) этой случайной величины равно:

a) 1,4; b) 1,7; c) 1,1; d) 1.

2. Дискретная случайная величина X имеет закон распределения вероятностей:

X	-1
P	0,4	0,6

Тогда математическое ожидание M(X) этой случайной величины равно:

a) 1; b) 1,4; c) 2,8; d) 2.

3. Дискретная случайная величина X имеет закон распределения вероятностей:

X	-5
P	0,5	0,5

Тогда математическое ожидание M(X) этой случайной величины равно:

a) 0,5; b) 0,5; c) 5,5; d) 2,75.

4. Дискретная случайная величина X имеет закон распределения вероятностей:

X	-3
P	0,2	0,8

Тогда математическое ожидание M(X) этой случайной величины равно:

a) 2,2; b) 1,0; c) 1,1; d) 2,0.

5. Дискретная случайная величина X имеет закон распределения вероятностей:

X	-2
P	0,3	0,7

Тогда математическое ожидание M(X) этой случайной величины равно:

a) 2,7; b) 1,35; c) 0,01; d) 1,5.

6. Формула

вычисления:

a) Математического ожидания; b)Дисперсии; c)Функции распределения; d) Плотности вероятности.

7. Формула

вычисления:

a) Функции распределения;

b) Дисперсии;

c) Плотности вероятности;

d) Математического ожидания.

8. Формула

вычисления:

a) Математического ожидания;

b) Дисперсии;

c) Плотности вероятности;

d) Функции распределения.

Дата добавления: 2014-12-27