
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип математической индукции
|
|
|
|
Математическая индукция
Ответы
Задачи для самостоятельного решения
1. Заданы предикаты
Р(x,y,z): 
Q(x,y,z): 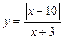
R(x,y,z): 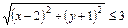
S(a,b,c): a нравится b больше, чем c
Запишите следующие высказывания: а) Р(1, 2, -5); б) Q(7,10); в) R(0,1); г) S(Миша, Марина, Таня).
2. Используя P,Q,R,S из упражнения 1, запишите высказывания:
а) 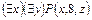 ; б)
; б) 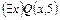 ; в)
; в) 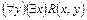 ; г)
; г) 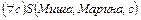 ; д)
; д) 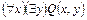 .
.
3. Пусть Q(x,y,z): 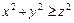 , предметная область для x, y, z– множество целых чисел. Что можно сказать об истинности
, предметная область для x, y, z– множество целых чисел. Что можно сказать об истинности  ?
?
4. Пусть P(x,y,z):  . Какой должна быть предметная область, чтобы следующее высказывание было истинным:
. Какой должна быть предметная область, чтобы следующее высказывание было истинным: 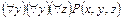
1. а) Р(1,2,-5): 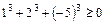 ; б)
; б) 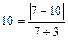 ; г) Мише Марина нравится больше, чем Таня. 2. а) существуют x и y такие, что
; г) Мише Марина нравится больше, чем Таня. 2. а) существуют x и y такие, что 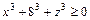 ; в) для каждого y существует x такое, что
; в) для каждого y существует x такое, что 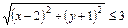 ; г) Мише нравится Марина больше, чем кто-либо. 3. Ложно, например, Q(1,2,3) – ложно. 4. Множество положительных действительных чисел.
; г) Мише нравится Марина больше, чем кто-либо. 3. Ложно, например, Q(1,2,3) – ложно. 4. Множество положительных действительных чисел.
(А1) Пусть P(n) – такое утверждение, что
1) P(1) истинно;
2) для каждого к, если P(k) истинно, то P(k+1) истинно
Тогда P(n) истинно для любого целого положительного числа n.
В символической записи:

Пример1. Доказать, что для любого натурального n выполняется
1+2+3+…+ n= 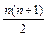
Пусть Sn – утверждение «1+2+3+…+ n= 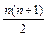 ». Проверим, что Sn истинно для n= 1.
». Проверим, что Sn истинно для n= 1.
1) S1 =1=  - верно;
- верно;
2) Предположим, что для любого к утверждение
Sк =1+2+3+…+к = 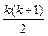 - верно.
- верно.
Требуется доказать, что Sк +1=1+2+3+…+ k + k +1= 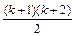 – верно. В самом деле, Sк +1=(1+2+3+…+ k)+ k +1= Sк +(k+1)=
– верно. В самом деле, Sк +1=(1+2+3+…+ k)+ k +1= Sк +(k+1)= 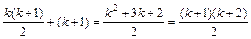 .
.
Итак, получили, что Sк +1истинно. Следовательно, по индукции, Sn истинно для всех натуральных n.
Пример 2. Требуется показать, что для любого положительного целого числа n, число n3- n делится на 3.
Пусть Sn – утверждение «n3 - n делится на 3». Покажем, что Sn истинно для n= 1.
1) S1 =13-1=0, поэтому n3 - n при n =1делится на 3, так как 0= 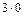 ,.
,.
Таким образом, S1 истинно.
2) Допустим, что Sk истинно, т.е. k3-k делится на 3, поэтому k3-k=3m для некоторого положительного целого m. Требуется доказать, что Sк +1 –истинно, т.е. (k+ 1 )3 -(k +1) делится на 3, т.е. существует такое натуральное w, что (k+ 1 )3 -(k +1)=3w.
Преобразуем
(k+ 1 )3 -(k +1)=(k3 +3 k2 +3 k +1)-(k +1)=(k3 - k)+(3 k2 +3 k)=3 m +3(k2 + k)=3w, где w= m +(k2 + k). Таким образом, (k+ 1 )3 -(k +1) делится на 3, и следовательно, Sк +1истинно. Поэтому, по индукции, Sn истинно для всех натуральных n.
(А2) ( Второй принцип индукции ). Пусть P(n) – утверждение. Если
а) Р(1) истинно, и
б) для произвольного k из истинности P(m) для всех m<k следует истинность P(k),
то P(n) истинно для всех положительных целых чисел n.
Аксиомы А1 и А2 сформулированы для целых чисел, начиная с 1, с продолжением условий на целые числа, больше 1. Аналогичные теоремы индукции верны для целых чисел, не меньших некоторого целого j, которое может не совпадать с 1.
Теорема (принцип индукции для целых чисел). Пусть P(n) - высказывание, обладающее свойствами
а) P(j) истинно и
б) для произвольного  , если P(k) истинно, то P(k+1) истинно.
, если P(k) истинно, то P(k+1) истинно.
Тогда P(n) истинно для каждого 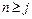 .
.
Пример3. Доказать, что для любого целого числа  имеет место неравенство
имеет место неравенство 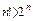
Решение. Согласно обозначениям, введенным для принципа индукции для целых чисел, имеем j=4, P(n) – утверждение «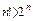 ».
».
1) При n=4 имеем 4!=24 и 24=16, так что 4!>24.
2) Предположим, что k!>2k. Нужно доказать, что (k+1)!>2k+1.
Заметим, что (k +1)!= k!(k +1); 2k+1=2k2, т.е нужно доказать, что k!(k +1)>2k2. Покажем, что k +1>2. Так как  , то k >2, следовательно, (k +1) k!>2·2k и (k +1)!>2k+1.. Таким образом, n!>2n для каждого
, то k >2, следовательно, (k +1) k!>2·2k и (k +1)!>2k+1.. Таким образом, n!>2n для каждого  .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!