Теоретические сведения. Задачи для самостоятельного решения

Задачи для самостоятельного решения

1. Докажите, что 1+4+7+10+…+(3 n -2)=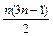

2. Докажите, что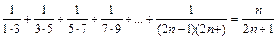

3. Докажите, что 1+2+2²+2³+…+2^n-1=2ⁿ-1

4. Докажите, что 1+ a + a² + a³ +…+ a^n-1 =

5. Докажите, что 1+3+5+7+…+(2 n -1)= n²

6. Докажите, что

7. Докажите, что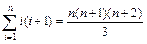

8. Докажите, что (n ³+11 n) делится на 6

9. Докажите, что (2^{5 n +1}+5 ^{n +2}) делится на 27

10. Докажите, что (5 ^{2n +1}+9·2 ⁿ⁺¹) делится на 23

11. Докажите, что (2^{2 n -1}-9 n²+ 21 n- 14) делится на 27

12. Докажите, что n² >2 n +1 для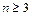

13. Докажите, что 2 ⁿ > n² для

14. Докажите, что для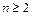

15. Докажите, что n!> n ³ для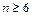

16. Докажите, что 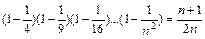для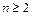

Раздел 2. Теория множеств

Под множеством понимается некоторая, вполне определенная совокупность объектов.

В общем случае множество задается путем указания характеристического свойства, т.е. свойства, которому удовлетворяют элементы данного множества, и только они. Например, множество нечетных цифр можно представить как: .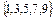

Если a есть один из объектов множества А, то говорят, что а есть элемент А, или а принадлежит А: 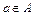. Если А не является элементом А, то .

Множество А есть подмножество множества В (), если каждый элемент А есть элемент В. Каждое множество есть подмножество самого себя.

Пустое множество (Ø)есть множество, которое не содержит элементов. Универсальное множество U есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.

Пересечением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат и А, и В: и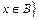

Пример1. Если А= , В= , то

Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В: или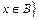

Пример 2. Найдем объединение множеств А и В (см. пример 1). , т.е. получено путем соединения вместе элементов А и В.

Разностью множеств А-В называется множество всех тех и только тех элементов А, которые не содержатся в В: 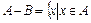и .

Симметрической разностью называется множество .

Пример 3. (условие см. пример 1). 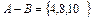, а .

Дополнение множества А – это множество элементов универсального множества, которые не принадлежат А: и .

Пример 4. Пусть U – множество натуральных чисел, 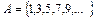- множество всех нечетных положительных чисел, тогда 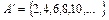- множество всех четных положительных чисел.

Для произвольных множеств А, В, С имеют место формулы:

а)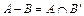

б)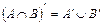

в)

г)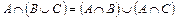

д)

Декартово произведение множеств А и В есть множество: 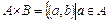и 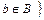. Объект (a,b) называется упорядоченной парой с первой компонентой а и второй компонентой b.

Порядок компонент в паре существенен!

Пример5. Пусть , ,

тогда .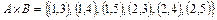

R – множество действительных чисел, 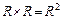- декартова плоскость (множество точек плоскости с заданными осями координат).

Если А или В – пустое множество, то 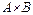- пустое множество.

Множество и операции над ними очень удобно изображать с помощью диаграмм Эйлера- Венна. Множества изображаются внутренними частями кругов, их пересечениями, объединениями и т.д. Универсальное множество изображается в виде прямоугольника.

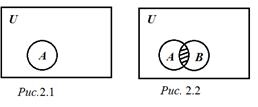
На рис.2.2 изображено пересечение множеств А и В.

На рис.2.3 изображено объединение множеств А и В; на рис. 2.4 штриховкой изображен результат разности множеств А-В.

Пример. Докажите, что 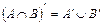с помощью диаграмм Эйлера-Венна.

Решение: Изобразим результат левой (рис.2.5) и правой (2.6) частей равенства штриховкой на диаграммах Эйлера- Венна.

Дата добавления: 2014-12-27