Теоретические сведения. 1. а) путь, простой путь, длина 5; б) путь, не простой путь, длина 6; в) путь, не простой путь, длина 7; г) путь

Ответы

1. а) путь, простой путь, длина 5; б) путь, не простой путь, длина 6; в) путь, не простой путь, длина 7; г) путь, не простой путь, длина 8.

2. а) не цикл; б) не цикл; в) цикл, не простой, длина 8; г) цикл, простой, длина 6.

3. а) вершины 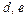- источники, б) вершины 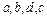- источники, вершина -сток.

4. а) и б) – деревья, в)- нет. 5. Высота дерева равна 3.

6. а) имеет эйлеров цикл.

Раздел 5. Элементы комбинаторики

Комбинаторика – раздел математики, в котором изучаются различные соединения (комбинации) элементов множеств. Наиболее существенную роль комбинаторика играет в тех областях математических знаний, где особенно часто встречаются «дискретные» совокупности объектов, в том числе в математической логике, теории графов, теории кодирования и пр.

Многие комбинаторные задачи могут быть решены с помощью двух следующих правил.

Правило умножения: если объект 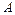можно выбрать 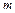способами, а объект 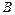может быть выбран 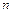способами, то выбрать пару « 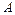и 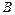» в указанном порядке можно 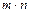способами.

Правило сложения: если объект 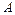можно выбрать 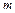способами, а объект 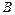- другими 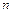способами при условии, что одновременный выбор 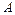и 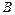невозможен, то выбор « 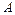или 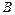» можно осуществить 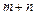способами.

Пример. Если в теннисной команде 5 мужчин и 3 женщины, то составить смешанную пару можно 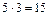способами, а выбрать одного спортсмена для участия в соревнованиях можно 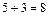способами.

При составлении различных комбинаций возможны две схемы выбора элементов из заданного множества:

- без повторений (выбранные элементы не возвращаются в исходное множество);

- с повторениями (на каждом шаге элемент возвращается обратно).

Рассмотрим множество, содержащее 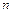различных элементов.

Размещением из 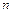элементов по 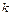элементам 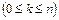называется любое упорядоченное подмножество данного множества, содержащее 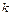элементов.

Перестановкой из 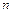элементов называется размещение из 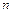элементов по 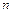элементам.

Сочетанием из 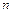элементов по 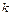элементам 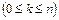называется любое подмножество данного множества, содержащее 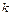элементов.

Формулы для нахождения числа данных комбинаций можно свести в следующую таблицу.

Вид комбинации	Наличие повторений
без повторений	с повторениями
Размещения (порядок важен)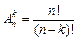
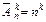
Перестановки (порядок важен)		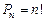перестановки вокруг	,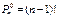
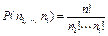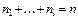
Сочетания (порядок не важен)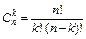

Отметим, что величина 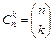называется также биномиальным коэффициентом, а величина 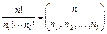- полиномиальным коэффициентом.

Пример. Рассмотрим множество из трех элементов .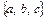

Составим всевозможные комбинации из двух элементов данного множества. Получим:

девять размещений с повторениями - ;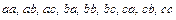

шесть размещений без повторений - ;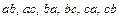

шесть сочетаний с повторениями - ;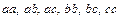

три сочетания без повторений - .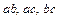

Дата добавления: 2014-12-27