Задачи для активного обучения

Задача 5.1. Сколько нечетных целых чисел находятся между числами 100 и 1000?

Решение. Используем комбинаторный принцип умножения: существует 5 вариантов выбора последней цифры числа (т. к. она должна быть нечетной); 10 вариантов выбора средней цифры и 9 вариантов выбора первой цифры. Таким образом, имеем 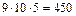нечетных чисел.

Задача 5.2. Сколькими способами можновыбрать две книги по разным темам, когда на полке находятся 15 книг по информатике, 12 книг по математике и 10 книг по химии?

Решение. Если выбирать книгу по информатике и книгу по математике, то существует возможностей. Если выбирать книги по информатике и по химии, то имеется 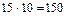способов. Для выбора книги по математике и книги по химии существует 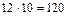возможностей. Следовательно, - число возможных способов выбора двух книг по разным темам.

Задача 5.3. Предположим, что команды 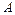и 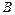участвуют в ежегодном турнире по волейболу, для победы в котором командам необходимо выиграть четыре игры из семи возможных. Если команда 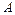выигрывает первые две игры, то сколько вариантов победы есть у команды 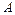и сколько у команды ?

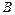Решение. Для того, чтобы представить возможные исходы построим дерево подсчета (см. рис. 5.1). Буква в каждой вершине обозначает команду, победившую в игре. Обведенная кружком буква обозначает команду, победившую в турнире.

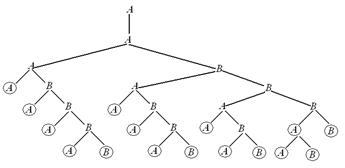
Рис. 5.1

По рисунку видно, что имеется десять исходов с победой команды 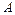и пять возможных исходов с победой команды .

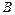Задача 5.4. Четверо студентов сдают экзамен. Сколькими способами могут быть им поставлены оценки, если никому не поставлена двойка?

Решение. Расстановка оценок в экзаменационной ведомости учитывает порядок следования фамилий студентов, поэтому используем размещения с повторениями (некоторые студенты могут получить одинаковые оценки): 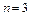(оценки – удовл., хор., отл.), (студенты), .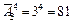

Задача 5.5. В профком университета избрали 9 человек. Сколькими способами из них можно выбрать председателя профкома и его заместителя?

Решение. В данном случае используем размещения без повторений: 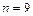(члены профкома), 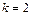(должности), 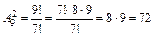(способа выбрать руководство профкома).

Задача 5.6. Сколькими способами можно рассадить 7 человек за круглым столом, если имеет значение только порядок соседей?

Решение. Сначала можно усадить одного человека. Этим исключается вращение, а оставшихся 6 человек можно рассадить 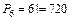способами.

Задача 5.7. В вазе стоят 9 красных и 7 белых гвоздик. Сколькими способами можно выбрать из них:

а) 5 гвоздик одного цвета; б) 4 красных и 3 белых гвоздики?

Решение. Порядок, в котором будут выбираться цветы, в данном случае не важен, поэтому будем использовать сочетания (без повторений, т.к. один и тот же цветок нельзя взять дважды).

а) выбрать красные гвоздики можно 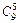способами, для выбора белых гвоздик существует 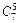возможностей, по правилу сложения получим

;

б) выбрать красные гвоздики можно 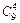способами и белые гвоздики - 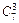способами, по правилу умножения получим

.

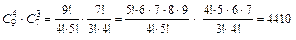Задача 5.8. Из 200 опрошенных людей, смотрящих телевизор, 110 человек смотрят спортивные передачи, 120 –комедии, 85 предпочитают драмы, 50 человек смотрят драмы и спорт, 70 –комедии и спорт, 55 смотрят комедии и драмы, 30 человек смотрят все виды передач. Сколько человек не смотрят ничего из вышеперечисленного?

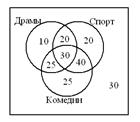Решение. Изобразим данную ситуацию с помощью диаграмм Эйлера-Венна. Тогда

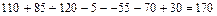
(количество человек, которые смотрят спорт, комедии и драмы),

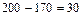(количество человек, которые не смотрят по телевизору ни спорт, ни драмы, ни комедии).

Дата добавления: 2014-12-27